Властивості задачі про призначення

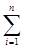
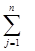Оскільки задача про призначення є окремим випадком транспортної задачі, то завжди шляхом уведення необхідної кількості фіктивних робіт або фіктивних верстатів можна від поданої задачі перейти до еквівалентної збалансованої. Тому надалі будемо розглядати задачу про призначення, у якій кількість верстатів дорівнює кількості робіт:

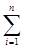F = c_ij x_ij ® min,

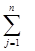
x_ij = 1, j = 1,n,

x_ij = 1, i = 1,n,

1;

x_іj =

0.

Теорема 14.1 (Про основну властивість задачі про призначення). Оптимальний розв’зок задачі про призначення не змінюється, якщо додати фіксовану величину до довільного стовпчика або до довільного рядка матриці вартостей.

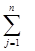
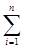Доведення. Нехай С - вихідна матриця, тоді для будь-якого допустимого розв’язку x⁰

F(x⁰) = c_ij x⁰_ij.

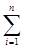
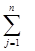
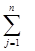
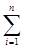
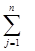
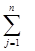
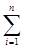
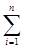Припустимо, що до усіх елементів кожного і-го рядка додається величина а_і, а кожного j-го стовпчика - величина bj. Тоді значення цільової функції на розв’язку дорівнює

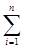
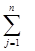F^’(x⁰) = (c_ij + а_і + bj)x⁰_ij = c_ij x⁰_ij + а_і x⁰_ij + bj x⁰_ij = F(x⁰) +

а_і + bj = F(x⁰) + const.

Таким чином, для кожного набора значень змінних x значення функцій F(x) і F^’(x) відрізняються на постійну величину. Тому сукупності наборів, на яких функції F(x) і F^’(x) досягають мінімуму, співпадають.

Надалі матриці вартостей, відповідаючі функціям F і F^’, будемо називати еквівалентними. Властивість, сформульована у теоремі 14.1, свідчить про те, що від початкової матриці завжди можна перейти до еквівалентної невід’ємної матриці, такої що у кожному рядку і у кожному стовпці знаходиться принаймні один нуль. Для цього треба у кожному рядку r від усіх елементів відняти мінімальний елемент рядка r, а у кожному стовпчику s від усіх елементів відняти мінімальний елемент стовпця s. Отримана таким чином матриця вартостей називається приведеною.

Приклад розв’язування задачі про призначення (перший етап)

Розглянемо приклад визначення приведеної матриці. Нехай вихідна матриця вартостей має вигляд

1 4 6 3

9 7 10 9

4 5 11 7

8 7 8 5.

Після віднімання від першого рядки числа 1, від другого – числа 7, від третього – числа 4 і від четвертого - числа 5 отримуємо матрицю

0 3 5 2

2 0 3 2

0 1 7 3

3 2 3 0.

Тепер для отримання приведеної матриці достатньо від елементів третього стовпця відняти число 3.

0 3 2 2

2 0 0 2

0 1 4 3

3 2 0 0

Згідно з угорським методом розв’язок задачі шукають на приведеній матриці. Зрозуміло, якщо вдається у отриманій матриці вибрати сукупність n нулів таким чином, щоб у кожному рядку та у кожному стовпчику знаходився один нуль сукупності, то розв’язок вихідної задачі знайдено. Тому на першому етапі угорського методу послідовно розглядаються рядки матриці і у кожному рядку, якщо можливо, вибирається нуль.

Надалі вибрані нулі будемо помічати символом “*”. Для поданого прикладу після першого етапу алгоритму отримуємо

0^* 3 2 2

2 0^* 0 2

0 1 4 3

3 2 0^* 0.

Дата добавления: 2014-01-13