Таким чином отримуємо

Множина можливих траекторій Т визначається способом вибору керувань у станах системи. Найбільш загальний спосіб задання правила для вибору керування полягає у тому, що задається вирішуюча функція (вирішуюче правило), яка визначається таким чином.

Розглянемо функцію h(t), визначену для усіх скінчених траекторій t Î Т. Позначимо стан, у який потрапляє система в результаті проходження траекторії t = ((i₀, u₀), (i₁, u₁), …, (i_k, u_k)), як tip(t) (tip(t) = g(u_k)). Функція h(t) називається вирішуючим правилом, якщо для усіх t Î Т h(t) Î N_tip(t).

Будемо говорити, що траекторія t = ((i₀, u₀), (i₁, u₁), …, (i_n, u_n)) визначається вирішуючим правилом h, якщо для кожного k = 1, n виконується співвідношення u_k = h(t_k), де t_k = ((i₀, u₀), (i₁, u₁), …, (i _k-1, u _k-1)) – скінчена траекторія, співпадаюча з початком траекторії t.

Множину траекторій, що визначаються довільним вирішуючим правилом, позначимо через T⁰. Назвемо вирішуюче правило стаціонарним, або політикою, якщо для будь-якої траекторії t h(t) = f(tip(t)), тобто керування, визначене вирішуючим правилом, залижить лише від кінцевого стану пройденої частини траекторії. Множину траекторій, що визначаються політиками, позначимо через T^p і розглянемо задачу пошуку максимуму функції F на траекторіях t Î Т^p, що починаються у стані i.

Позначимо множину таких траекторій через T(i), а множину траекторій, що починаються з пари (i, u) через T(i, u). Припустимо,

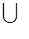V(i) = max { F(t) | t Î Т(i)}. (16.2)

Оскільки T(i, u), u Î N_i утворюють розбиття множини Т(i): Т(i) = T(i, u),

" u Î N_i

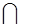T(i, u_j) T(i, u_k) = Æ, " u_j ¹ u_k, то

V(i) = max { max {F(t) | t Î T(i, u)} | u Î N_i }.

Враховуючи, що F(t) рекурентна, для кожної траекторії t Î Т(i, u) можна записати

F(t) = c (u) + b (u) x F(t^’ ).

Перший доданок у правій частині має однакове значення для кожної траекторії з T(i, u), тому його можна винести за знак максимуму. Аналогічно можна винести за знак максимуму і множник b (u):

V(i) = max { c (u) + b (u) max {F(t^’) | t Î T(i, u)} | u Î N_i }.

Для стаціонарного вирішуючого правила множина траекторій t^’ співпадає з множиною T(g(u)), і тому max {F(t^’) | t Î T(i, u)}= max {F(t) | t Î T(g (u)) } = V(g (u)).

max { c (u) + b (u) V(g (u) | u Î N_i }, якщо N_i ¹ Æ;

V(i) = (16.3)

F(i) при N_i = Æ,

де F(i) значення цільової функції на пустій траекторії, при умові, що система знаходиться у стані i.

Рівняння (16.3) називається рівнянням динамічного програмування або рівнянням Белмана, названим на честь автора динамічного програмування, американського математика Белмана. Ця формула дає змогу обчислювати значення цільової функції на ускладнених траєкторіях, використовуючи значення на спрощенних траекторіях.

Приклад розв’язування задачі методом динамічного програмування.

Розглянемо відому комбінаторну задачу про рюкзак, яка відіграла значну роль у розвитку методів дискретної оптимізації. Спочатку зупинемося на одновимірному варіанті цієї задачі, що формулюється таким чином.

Турист, готуючись до подорожі, збирає рюкзак, у який можна покласти вантаж, сумарною вагою не більше а кг. Цей вантаж може складатися з предметів n типів. Предмет і-го типу (і = 1, n) має вагу а_і і цінність с_і. Треба визначити кількість предметів кожного типу, які турист повинен покласти у рюкзак, щоб отримати максимальну сумарну цінність предметів.

Побудуємо математичну модель задачі. Уведемо цілі змінні x_i – кількість предметів і-го типу, покладених у рюкзак (і = 1, n). Тоді цільова функція приймає вигляд

F = с_і x_i ® max.

Обмеження на сумарну вагу предметів у рюкзаку можна врахувати за допомогою нерівності

а_і x_i £ а.

Дата добавления: 2014-01-13