Тема 2. Мінори та алгебраїчні доповнення. Обернена матриця

Контрольні запитання

1. Що називається мінором матриці, як можна розкласти визначник через мінори?

2. Як понизити порядок визначника?

3. Що називається оберненою матрицею, як її знайти?

4. Сформулюйте теорему про існування оберненої матриці.

5. Що називається рангом матриці?

6. Що таке лінійна залежність та лінійна незалежність рядків матриці?

План.

1. Мінори та алгебраїчні доповнення. Мінор матриці.

2. Обернена матриця та її знаходження.

3. Ранг матриці.

1. Нехай маємо визначник третього порядку .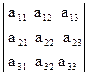

Мінором, який відповідає даному елементові визначника третього порядку, називається визначник другого порядку, який одержується в результаті викреслення рядка і стовпця на перетині яких розміщений даний елемент. Позначаємо, наприклад, M₂₁- мінор, який відповідає елементові а₂₁: M₂₁=.

Алгебраїчним доповненням деякого елемента визначника третього порядку називається його мінор, взятий зі знаком «плюс», якщо сума номерів рядка і стовпця, на перетині яких знаходиться даний елемент, парна, і взятий зі знаком «мінус», якщо сума номерів рядка і стовпця, на перетині яких знаходиться даний елемент, непарна:

A_ij = (-1)^i+jM_ij.

Теорема (про розклад визначника по елементах деякого рядка або стовпця): Визначник третього порядку дорівнює сумі добутків всіх елементів деякого рядка (стовпця) на їх алгебраїчні доповнення.

Доведення.

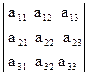= a₁₁ a₂₂ a₃₃ + a₂₁ a₃₂ a₁₃ + a₁₂ a₂₃ a₃₁ - a₁₃ a₂₂ a₃₁ - a₂₁ a₁₂ a₃₃ - a₂₃ a₃₂ a₁₁ = = a₁₁(a₂₂a₃₃-a₃₂a₂₃) - a₁₂(a₂₁a₃₃-a₃₁a₂₃) + a₁₃(a₂₁a₃₂-a₂₂a₃₁) =

= a₁₁ A₁₁+ a₁₂A₁₂+ a₁₃A₁₃.

Наслідок: Сума добутків елементів деякого рядка (стовпця) на алгебраїчні доповнення відповідних елементів іншого рядка (стовпця) дорівнює 0.

Визначники вищих порядків (четвертого, п’ятого,...) можна також розписувати за їхніми алгебраїчними доповненнями, поступово понижуючи порядок і зводячи до визначників третього чи другого порядку.

2. Розглянемо квадратну матрицю n-го порядку А=.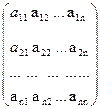

Квадратна матриця A називається невиродженою (неособливою), якщо її визначник не дорівнює 0 і виродженою (особливою), якщо її визначник дорівнює 0. |А| або detA- позначення визначника матриці А.

Оберненою матрицею до квадратної матриці А називається матриця А^-1, яка задовольняє такій умові А^-1А=АА^-1=Е.

Теорема. Для того, щоб квадратна матриця А мала обернену матрицю, необхідно і досить, щоб вона була невиродженою, тобто, щоб |А|№0.

Доведення.

1). Необхідність.

Дано: матриця А має обернену матрицю А^-1.

Довести: |А|№0.

Припустимо, що визначник дорівнює 0. Тоді, з одного боку, |АА^-1| = |А| |А^-1| = 0; з іншого боку, оскільки А^-1А=АА^-1=Е, то |АА^-1| = |Е| = 1. Ми прийшли до суперечності, отже, |А|№0.

2) Достатність.

Дано: |А|№0.

Довести існування оберненої матриці.

Для простоти викладу доведення проведемо на прикладі матриці третього порядку

А=.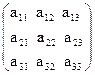

Складемо матрицю з алгебраїчних доповнень і транспонуємо її: В=. В^Т=. Поділимо кожен елемент матриці В^Т на визначник |А|.

Одержимо матрицю і доведемо, що вона є оберненою, помноживши її на матрицю А.

=

=

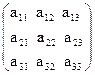
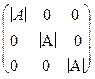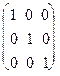= == Е. Аналогічно доводиться, що А^-1А=Е.

Отже, матриця виду є оберненою до матриці А.

Дане доведення теореми дає також спосіб знаходження оберненої матриці.

3. Нехай дано матрицю А=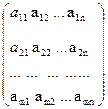. Виберемо довільних k рядків та k стовпців, які менші за порядок матриці. Елементи, які розміщенні на перетині вибраних рядків і стовпців утворюють квадратну матрицю порядку k. Визначник, який відповідає даній матриці називають мінором k-го порядку.

Рангом матриці називають найвищий порядок нерівних нулю мінорів. Позначають r(A), чи rang A.

Елементарними перетвореннями матриці називають:

1. Перестановку двох рядків або стовпців.

2. Множення всіх елементів деякого рядка або стовпця на одне і те ж число, не рівне 0.

3. Додавання до елементів деякого рядка (стовпця) відповідних елементів іншого, помножених на одне і те ж число.

Можна довести таку теорему:

Якщо зробити елементарні перетворення над матрицею А, то отримаємо матрицю, ранг якої дорівнює рангові матриці А.

Базисним мінором матриці називають мінор, який не рівний 0 і порядок якого дорівнює рангу матриці.

Нехай дано А=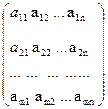. Розглянемо рядки матриці:

с₁= (a₁₁, a₁₂,..., a_1n), c₂=(a₂₁, a₂₂,..., a_2n),......., c_m=(a_m1, a_m2,...., a_mn).

Рядки матриці А називаються лінійно залежними, якщо існують такі чсила g₁, g₂,..., g_m не всі рівні нулю, для яких виконується рівність

g₁с₁+ g₂с₂+...+ g_mс_ь=0 - (нульовий рядок). (1.1)

Якщо рівність (1.1) виконується лише тоді, коли всі g_і=0, то рядки матриці називаються лінійно незалежними.

Теорема. Максимальне число лінійно незалежних рядків матриці А дорівнює максимальному числу лінійно незалежних стовпців матриці А і дорівнює рангу цієї матриці.

На практиці, як правило, шукають лінійно незалежні рядки чи стовпці і від них роблять висновок про ранг матриці.

Дата добавления: 2014-01-13