Система (сукупність) векторів A1, A2, … , Ar (r 2) називається лінійно залежною, якщо існують такі числа k1, k2, … , kr, серед яких не усі дорівнюють нулю, що має місце рівняння

Вираз вигляду kjAj називається лінійною комбінацією векторів A1, A2, …, Ar.

Лінійна залежність векторів

Arccos.

|A| |B|

k_jA_j = 0. (3.1)

Якщо вказані числа не існують, система векторів називається лінійно незалежною. Для лінійно незалежної системи векторів A₁, A₂, …, A_r з рівняння (3.1) прямує k_j = 0 для усіх j.

Максимальна кількість лінійно незалежних векторів, що належать поданій системі, називається рангом системи векторів.

Ранг матриці – порядок максимальної квадратної підматриці її, визначник якої не дорівнює нулю.

Теорема 3.1. (Про ранг системи векторів). Нехай подана система векторів V = { а_1, а_2, …, a_m }:

а₁ = (а_11, а_12, …, a_1n),

а₂ = (а_21, а_22, …, a_2n),

а_m = (а_m1, а_m2, …, a_mn).

Побудуємо матрицю A на координатих цих векторів як на елементах:

а₁₁ а₁₂ … a_1n

A = а₂₁ а₂₂ … a_2n

а_m1 а_m2 … a_mn

Тоді ранг матриці A дорівнює рангу системи векторів V: rank(V) = rank(A).

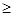Доведення. Спочатку доведемо, що rank(V) rank(A). Нехай rank(A) = r. Це означає, що матриця А містить квадратну підматрицю B порядку r, визначник якої не дорівнює нулю. Без втрати загальності можна припустити, що ця підматриця розташована у верхньому лівому куту, оскільки цієї умови завжди можна досягти, змінивши порядок векторів у системі та порядок координат векторів. B

а₁₁ а₁₂ … a_1r … a_1j … a_1n

а₂₁ а₂₂ … a_2r … a_2j … a_2n

A = а_r1 а_r2 … a_rr … a_rj … a_rn

а_i1 а_i2 … a_ir … a_ij … a_in

а_m1 а_m2 … a_mr … a_mj …a_mn

Оскільки визначник матриці B не дорівнює нулю (|B| 0), перші r рядків матриці A лінійно незалежні. Дійсно, якби ці рядки були лінійно залежні, то і рядки матриці B були лінійно залежні, що суперечить умові |B| 0.

Тепер доведемо, що rank(V) rank(A). Для цього покажемо, що коли додати до перших r рядків матриці A довільний рядок цієї матриці, то отримаємо лінійно залежну систему рядків.

Розглянемо квадратну підматрицю B^’ матриці A порядку r+1, що утворена матрицею B, доповненою елементами довільного j-го стовпця та довільного i-го рядка.

а₁₁ а₁₂ … a_1r a_1j

а₂₁ а₂₂ … a_2r a_2j

B^’ =

a_r1 а_r2 … a_rr a_rj

а_i1 а_i2 … a_ir a_ij

Визначник матриці B^’ дорівнює нулю, оскільки rank(A) = r. Розкладемо його за елементами j-го стовпця:

а_1jA_1j + а_2jA_2j + … + a_rjA_rj + a_ijA_ij = 0,

де A _sj (s = 1, r, s = i) – відповідні алгебраїчні доповнення. Оскільки A_ij 0, маємо

a_ij = -а_1jA_1j /A_ij - а_2jA_2j /A_ij - … - a_rjA_rj /A_ij =

= k ₁а_1j + k ₂а_2j + … + k _r a_rj,

де k _s = - A _sj /A_ij , s = 1, r.

Підставляючи у матрицю B^’ послідовно елементи усіх стовпців матриці A (j = 1, n), отримуємо

a_i1 = k ₁а₁₁ + k ₂а₂₁ + … + k _r a_r1,

a_i2 = k ₁а₁₂ + k ₂а₂₂ + … + k _r a_r2,

a_in = k ₁а_1n + k ₂а_2n + … + k _r a_rn.

Останню систему рівнянь можна записати у вигляді

a_i = k ₁а₁ + k ₂а₂ + … + k _r a_r,

тобто i-й рядок є лінійною комбінацією перших r рядків, і цим завершується доведення.

Оскільки при транспонуванні матриці ранг її не змінюється, то максимальна кількість лінійно незалежних стовпчиків у матриці A також дорівнює r.

Наслідок. Будь-яка система, що містить n+1 n-вимірних векторів, лінійно залежна.

Дійсно, побудувавши на компонентах цих векторів як на елементах матрицю А, отримуємо матрицю розміру n+1 х n, ранг якої, очевидно, менше n+1.

Базис n-вимірного лінійного векторного простору

Базисом n-вимірного лінійного векторного простору називається сукупність n лінійно незалежних векторів цього простору.

Теорема 3.2. (Про розкладання вектора за базисом.) Кожний вектор n-вимірного лінійного простору можна записати у вигляді лінійної комбінації базисних векторів і тільки одним чином.

Доведення. Нехай E₁, E₂, …, E_n - базис. Візьмемо довільний вектор A. Система векторів E₁, E₂, …, E_n, A лінійно залежна. Тому k₀A + k₁E₁ + k ₂E₂ + … + k _nE_n = 0, де не усі k_j (j = 0, n) дорівнюють нулю. Число k₀ не дорівнює нулю, оскільки інакше вектори E₁, E₂, …, E_n були б лінійно залежні. Тому

A = (-k₁/k₀ )E₁ + (-k ₂/k₀)E₂ + … + (-k _n/k₀)E_n , (3.2)

Дата добавления: 2014-01-13