Після віднімання від (3.3) рівняння (3.2) маємо

Тепер доведемо, що розкладання за поданим базисом тільки одне. Припустимо, що крім розкладання (3.2), існує інше

Тобто A – лінійна комбінація векторів базису.

A = s₁E₁ + s ₂E₂ + … + s _nE_n . (3.3)

0 = (s₁+k₁/k₀ )E₁ + (s₂+k ₂/k₀)E₂ + … + (s _n+k _n/k₀)E_n.

Оскільки лінійні комбінації (3.2) і (3.3) відрізняються принаймні одним коефіцієнтом, останнє рівняння суперечить лінійній незалежності базисних векторів, і цим завершується доведення..

Лінійний векторний простір може мати багато базисів. Серед них виділяють один - ортонормований базис:

e₁ = (1, 0, …, 0),

e₂ = (0, 1,..., 0),

e_n = (0, 0, …, 1).

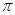Ці вектори, очевидно, лінійно незалежні. Довжина кожного дорівнює одиниці, а скалярний добуток довільних двох різних векторів дорівнює нулю, і це означає, що кут між ними становить /2. Коефіцієнти розкладання будь-якого вектора за ортонормованим базисом є компонентами цього вектора

A = (a₁, a ₂, … a _n) = a₁e₁ + a ₂e₂ + … + a _ne_n.

Тепер повернемося до аналізу методу Жордана-Гауса. У результаті застосування методу вихідна матриця A коефіцієнтів системи рівнянь перетворюється. Позначимо сукупність стовпчиків, що відповідать вилученним змінним, як матрицю B. В результаті застосування методу Жордана-Гауса до сумісної системи стовпчики матриці B перетворюються у одиничні стовпчики. Сукупність цих одиничних стовпчиків утворює одиничну матрицю з, можливо, переставленими стовпцями. Отримати таку матрицю можна шляхом множення матриці B на обернену B^-1 і потім на перестановочну матрицю P. Перестановочна матриця містить елементи, що дорівнюють нулю або одиниці, і у кожному рядку та у кожному стовпчику міститься тільки одна одиниця. Оскільки множення матриць асоціативне, можна вважати, що у результаті виконання методу Жордана-Гауса матриця B помножається на матрицю B^-1~ = B^-1 P. А це, у свою чергу, означає, що і уся матриця A помножається на B^-1~ . Умовно систему Ах = b можна записати у вигляді [B R]x = b. Умовність полягає у тому, що у матриці А стовпці матриці B можуть довільним чином чергуватися із стовпцями матриці R. Результат перетворення системи можна записати у вигляді [B^-1~ B B^-1~R] x = B^-1~b.

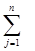Існування для матриці B оберненої матриці B^-1 означає, що її стовпці лінійно незалежні і тому утворюють базис у просторі стовпців (m-вимірних векторів, якщо матриця B має порядок m). Саме це виправдовує раніше застосований термін “базисні змінні”, оскільки ці змінні відповідають базисним стовпчикам.

Вихідну систему рівнянь можна уявити у вигляді а^j х_j = b, де а^j - j-й стовпець матриці A. Таким чином шукані змінні – це коефіцієнти лінійної комбінації стовпців матриці A, що дорівнює вектору правих частин рівнянь. Базисний розв’язок являє коефіцієнти розкладання вектору b за базисними стовпцями. Якщо усі базисні змінні не дорівнюють нулю, то базисний розв’язок називають невиродженим. У іншому разі базисний розв’язок вироджений. Геометричний смисл виродження полягає у тому, що вектор b є лінійною комбінацією деякої власної підмножини множини базисних стовпців.

Форма системи рівнянь, отримана після застосування метода Жордана-Гауса, називається приведеною. Кожному базису у просторі стовпців відповідає своя приведена форма. Всього таких форм існує стільки, скільки різних базисів можна утворити зі стовпців матриці A. Якщо ранг матриці A дорівнює m, кількість стовпців – n, то максимальна можлива кількість різних базисів дорівнює C^m_n = n!/(m!(n-m)!). У конкретному випадку кількість базисів може виявитися меншою, оскільки не усі сукупності з m стовпців можуть бути лінійно незалежними.

Дата добавления: 2014-01-13