Оценка параметров распределения

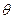Определение 72. Статистической оценкой параметра теоретического распределения называют его приближенное значение, зависящее от выборки: 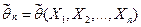. Функцию результатов наблюдений называют статистикой.

Оценка является случайной величиной, так как является функцией независимых случайных величин 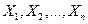; если произвести другую выборку, то функция 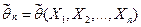примет другое значение. Если число наблюдений мало, замена параметра его оценкой, например математического ожидания средним арифметическим, прводит к ошибке. К оценке любого параметра предъявляется ряд требований, которым должна удовлетворять оценка хорошего качества: несмещенность, состоятельность и эффективность.

Определение 73. Если математическое ожидание 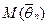равно нулю, то оценка называется несмещенной. В противном случае – смещенной. Если 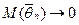, то оценка называется асимптотически несмещенной.

Требование несмещенности важно при малом числе наблюдений и указывает на отсутствие систематической ошибки.

Определение 74. Оценка параметра 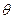называется состоятельной, если она сходится по вероятности к оцениваемому парметру: .

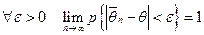Требование состоятельности указывает на приближение оценки к истинному значению параметра 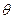с ростом числа наблюдений. Состоятельность оценки может быть установлена с помощью следующей теоремы.

Теорема 29 Если оценка параметра 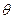является несмещенной и , то - состоятельная оценка.

Определение 75. Несмещенная оценка параметра 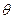называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра .

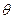На практике не всегда удается подобрать оценки удовлетворяющие всем трем критериям. Рассмотрим далее точечные оценки таких параметров распределения как математическое ожидание и дисперсия, т.е. эти числа будем определять по выборке.

Пусть 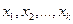- выборка, полученная в результате проведения независимых наблюдений за случайной величиной 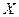. Представим значения 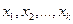случайной величины в виде 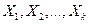, т.е. под 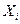будем понимать значение случайной величины 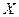в i-ом наблюдении. Эти случайные величины можно рассматривать как независимых случайных величин. Поэтому: 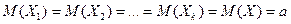и .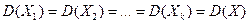

Теорема 30 Если 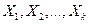- выборка из генеральной совокупности и 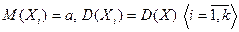, то выборочное среднее 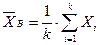- несмещенная и состоятельная оценка математического ожидания .

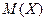Теорема 31 Если 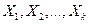- выборка из генеральной совокупности и 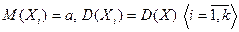, то исправленная выборочная дисперсия 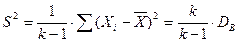- несмещенная и состоятельная оценка дисперсии .

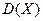Следует отметить, что относительная частота появления случайного события A в независимых наблюдениях является несмещенной, состоятельной и эффективной оценкой вероятности этого события.

В случае когда объем выборк невелик точечные оценки приводят к ошибкам, т.к. дают большую погрешность. Этого недостатка лишены интервальные оценки неизвестного параметра 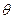, т.е. те, которые определяются концами интервала.

Определение 76. Интервал 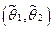, покрывающий с вероятностью 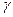истинное значение параметра 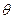, называется доверительным интервалом, а 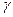- надежностью оценки или доверительной вероятностью.

Чаще всего доверительный интервал выбирают симметричным относительно несмещенной точечной оценки параметра 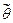, т.е. 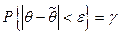, где число 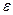характеризует точность оценки. Надежность 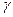принято выбирать равной 0,9; 0,95; 0,99; 0,999, т.е. когда нахождение оцениваемого параметра в доверительном интервале почти достоверно.

Рассмотрим построение интервальных оценок для параметров нормального распределения: математического ожидания и среднего квадратического отклонения.

Построим доверительный интервал для математического ожидания случайной величины 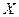при известной дисперсии.

Пусть 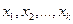- выборка, полученная в результате проведения независимых наблюдений за случайной величиной 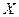, для которой известно среднее квадратическое отклонение 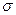. Зададим доверительную вероятность равной 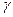. Оценкой математического ожидания является выборочное среднее 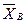, которое как и сама величина 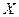распределено по нормальному закону.

Рассмотрим случайную величину 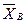. Определим параметры её распределения:

, .

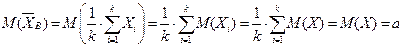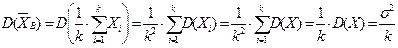Используем формулу теории вероятностей вероятности попадания в интервал для нормально распределенной случайной величины: 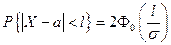. Тогда для случайной величины 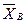имеем: 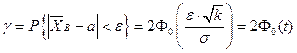, где 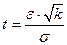. Из последнего равенства находим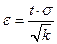

(из этой формулы следует, что с возрастанием объема выборки точность оценки увеличивается, а увеличение надежности уменьшает точночть оценки), следовательно 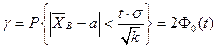. Таким образом, интервал 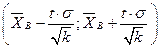- доверительный интервал для 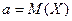. Поскольку 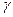было задано, то по таблице значений функции Лапласа из равенства находим аргумент t.

Построим доверительный интервал для математического ожидания случайной величины 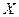при неизвестной дисперсии.

Пусть 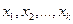- выборка, полученная в результате проведения независимых наблюдений за случайной величиной 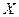, для которой известно среднее квадратическое отклонение 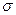. Зададим доверительную вероятность равной 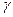. Оценкой математического ожидания является выборочное среднее 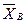, которое как и сама величина 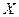распределено по нормальному закону: .

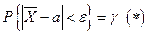Рассмотрим вспомогательную случайную величину 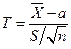, (где S – исправленное среднее квадратическое отклонение 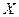, вычисленное по выборке), которая имеет распределение Стьюдента с n-1 степенями свободы. Перейдём в неравнстве 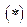от случайной величины 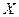к случайной величине 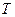: 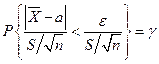или 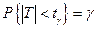. По таблице квантилей распределения Стьюдента при данной доверительной вероятности 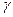и числе степеней свободы n-1, найдем значение 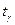. Из равенства 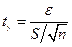находим 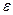. Тогда неравенство 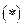можно переписать в следующем виде: 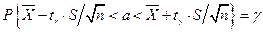, т.е. доверительным интервалом для математического ожидания при неизвестном среднем квадратическом отклонении и доверительной вероятностью 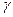будет интервал .

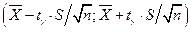Построим доверительный интервал для среднего квадратического отклонения. Пусть 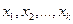- выборка, полученная в результате проведения независимых наблюдений за случайной величиной 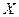, для которой известно математическое ожидание . Зададим доверительную вероятность равной 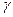. Оценкой среднего квадратического отклонения является 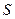: 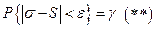. Рассмотрим вспомогательную случайную величину 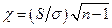, квадрат которой распределен по закону 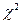с n-1 степенями свободы. Перейдем в неравенстве 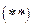к случайной величине :

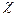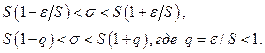
По таблице приложения вычисляем 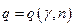и подставляем в последнее неравенство, т.е. доверительным интервалом для среднего квадратического отклонения при известном математическом ожидании является интервал 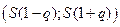. Если же , то доверительным интервалом будет .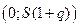

Дата добавления: 2014-01-11