Предмет и задачи теории массового обслуживания

Лекция 115

Тема № 58. Системы массового обслуживания (СМО)

Занятие №1.Общие сведения о СМО.

1. Предмет и задачи теории массового обслуживания.

2. Классификация систем массового обслуживания.

3. Потоки событий, их свойства и математическое описание.

4. Случайный процесс со счетным множеством состояний.

5. Марковский случайный процесс.

Литература

Вентцель Е.С. Теория вероятностей. – М.: Издательский центр «Академия», 2003г. стр. с.506-527

Достаточно широкий класс сложных систем образуют так назы­ваемые системы массового обслуживания (СМО). Характерными осо­бенностями этих систем являются:

- наличие объектов, нуждающихся, вообще говоря, в случайные
моменты времени в обслуживании, т.е. нуждающихся в выполнении
некоторых работ над собой или для себя; совокупность указанных
объектов можно рассматривать как источник случайного потока
заявок (требований) на обслуживание;

- наличие объектов, которые производят обслуживание и назы­ваются обслуживающими приборами или каналами обслуживания;

- возникновение задержек в обслуживании (образование очере­ди на обслуживание), если в момент поступления очередного требования все приборы заняты обслуживанием ранее поступивших.

В качестве объектов обоих типов могут выступать люди, приборы, агрегаты, системы, т.е. любые материальные объекты. Теория массового обслуживания - это математический аппарат, развитый для построения математических моделей СМО и их иссле­дования. Исторически она развивалась как ветвь теории вероят­ностей. Задача теории массового обслуживания заключается в разработке методов установления зависимости между параметрами СМО и показателями эффективности ее функционирования.

Зарождение и развитие теории массового обслуживания связано с анализом пропускной способности телефонных линий. Видный датский инженер и математик А.К. Эрланг (1878-1929 гг.), занижавшийся изучением этих проблем, опубликовал результаты своих исследований в 1917 г.

Развитие средств связи, науки, техники и экономики расширя­ло круг задач, для решения которых использовались метода тео­рии массового обслуживания стимулировало развитие самой тео­рии. В настоящее время в качестве своеобразных СМО могут рас­сматриваться; вычислительные центры и отдельные цифровые вычислительные машины; системы сбора и обработки информации автоматизированные производственные цехи, поточные линии, ремонтные мастерские; транспортные системы; предприятия торговли, бытового обслуживания и учреждения здравоохранения.

К СМО могут быть отнесены и войсковые системы, создаваемые для поражения противника, организация связи и управления вой­сками, ремонта и восстановления техники, дезактивации личного состава и т.д., т.е. те системы, где поступают заявки (вызовы) в случайные моменты времени, которые должны быть обслужены (поражены, восстановлены и т.п.).

Большой вклад в развитие теории массового обслуживания внесли русские и советские ученые: А.А. Марков (1856-1922), А.Я. Хинчин (1894-1959), академик АН УССР Б.В. Гнеденко, член-корр. АН СССР Н.П. Бусленко, Е.С. Вентцель, И.Н. Кова­ленко, Б.А. Севастьянов, Ю.В. Прохоров.

ЗРК, ремонтное предприятие ГРАУ могут быть представлены, как СМО.

В данном пособии будут рассмотрены элементы теории массового обслуживания и особенности ее применения для решения практических задач проектирования и оценки эффективности в военном деле.

2 Классификация систем массового обслуживания

Для задания системы массового обслуживания необходимо указать:

- кого (что) обслуживает система – входящий поток заявок;

- кто (что) производит обслуживание – множество обслуживающих приборов;

- как (по каким правилам) происходит обслуживание – дисциплину обслуживания.

Обобщенная схема СМО представлена на рис. 2, где сплошной стрелкой показан входящий поток заявок, а штриховыми стрелками – возможные пути движения заявок. Кружками на этой схеме показаны заявки, ожидающие обслуживания и очереди. Путь, по которому пройдет заявка, поступившая в систему, определяется характером заявки, сущностью процесса обслуживания и принятой в СМО дисциплиной обслуживания.

Обслуженные заявки

Из сказанного следует, что основными классификационными признаками, определяющими тип СМО, могут быть:

- характер входящего потока заявок;

- структура множества обслуживающих приборов и их основные характеристики;

- дисциплина обслуживания.

Классификация СМО по перечисленным признакам показана на рис. 3. Рассмотрим более подробно каждый из этих факторов.

Входящий поток – последовательность заявок, поступающих на обслуживание в случайные моменты времени. Часто заявку отождествляют с ее материальным носителем: поток донесений, поступающих на обработку в штаб; поток информации, поступающий на обработку в ЦВМ; поток самолетов, налетающих на объект, прикрываемый средствами ПВО; поток приборов, агрегатов, машин, поступающих в ремонтную мастерскую, и т.д.

Если с точки зрения обслуживания все заявки равноправны, то они отличаются друг от друга только моментами поступления и образуют однородный входящий поток. Каждой заявке можно поставить в соответствие точку на оси вращения (рис. 4).

Наиболее полной характеристикой входящего потока является многомерный закон распределения моментов поступления заявок t₁,t₂,…,t_k или интервалов времени между заявками z₁=t₁, z₂=t₂-t₁,…

При исследовании СМО необходимо учитывать, является ли поток заявок ограниченным и зависят ля его параметры от процесса обслуживания. СМО, у которых входящий поток заявок является неограниченным, называются разомкнутыми. СМО с ограниченным потоком заявок называются замкнутыми.

Типичным примером замкнутой СМО является система «вычислительные устройства – инженеры по ремонту», например, в крупном вычислительном центре, в которой инженеры-ремонтники обслуживают конечную группу устройств. В этой системе поток устройств, требующих ремонта, существенно зависит от процесса обслуживания: очередная заявка может поступить на ремонт устройства только после устранения предыдущей неисправности, т.е. общее число заявок не может превысить число вычислительных устройств.

Обслуживающий прибор (канал) – это материальный объект или совокупность материальных объектов, одновременно участвующих в обслуживании заявки.

При рассмотрении СМО всегда предполагается, что прибор в каждый момент времени может обслужить только одну заявку. Пример - оптический канал наведения ПТРК может одновременно наводить только один ПТУР, это типичный пример одноканальной СМО.

Ракетный комплекс имеющий в своем составе несколько пусковых установок- типичный пример многоканальной СМО.

Основным параметром обслуживающего прибора является время обслуживания заявки, которое в общем случае представляет собой случайную величину и поэтому полностью определяется законом ее распределения.

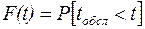, (2.1)

где P[t_обсл<t] – вероятность того, что время обслуживания не превосходит некоторой величины t. Очевидно, что обслуживающий прибор можно рассматривать как источник потока обслуженных заявок. Параметры этого потока определяются законом (2.1), входящим потоком и дисциплиной обслуживания.

Обычно полагают, что обслуживающий прибор может находиться только в двух состояниях: «занят», «свободен». Однако в реальных системах необходимо учитывать также и другие возможности:

- к обслуживанию очередной заявки прибор может приступать только через некоторое время (вообще говоря, случайное) время после обслуживания предыдущей заявки (например, артиллерийское орудие необходимо перезарядить);

- для перехода прибора из состояния «свободен» в состояние «занят» требуется также некоторое время (например, прогрев прибора перед работой);

- во время обслуживания приборы могут выходить из строя.

Способы учета указанных возможностей зависят от конкретных условий решаемой задачи.

В дальнейшем мы всегда будем предполагать, что время обслуживания – это время от начала момента обслуживания заявки до момента готовности прибора к обслуживанию очередной заявки.

При рассмотрении множества обслуживаемых приборов необходимо учитывать:

- число обслуживаемых приборов;

- взаимное расположение приборов и взаимосвязь между ними в процессе обслуживания заявок;

- полнодоступность системы, т.е. возможность обслуживания каждым прибором любой заявки (если это условие не выполняется, то система является неполнодоступной);

- однотипность обслуживаемых приборов (приборы однотипны, если характеризуются одним и тем же законом распределения времени обслуживания).

Перечисленные факторы определяют структуру СМО.

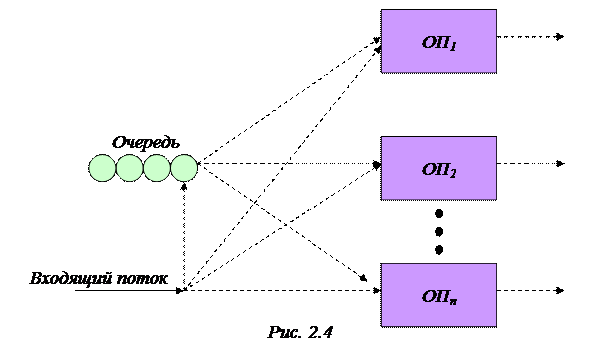
По числу обслуживающих приборов различают одноканальные многоканальные системы массового обслуживания. Многоканальная СМО схематически изображена на рис. 2.4. В этой системе все обслуживающие приборы (ОП) выполняют однородные операции обслуживания, т.е. осуществляется параллельное обслуживание. Заявка считается обслуженной системой, если она обнаружена одним из ее каналов (приборов).

Пример двухканальной СМО –

боевая машина ЗПРК «Панцирь»,

может одновременно наводить две

ракеты на две цели.

Если обслуживание заявки должно осуществляться последовательно несколькими приборами, то такие системы называют многофазными. СМО, изображенная на рис. 2.4, является однофазной. Схема многоканальной однофазной СМО показана на рис. 2.5. В этой системе обслуживание заявки осуществляется последовательно, перед каждым ОП может создаваться своя очередь. Заявка считается обслуженной, если прошла все фазы обслуживания. Типичными примерами многофазных СМО являются технологические потоки сборки (ремонта) приборов, агрегатов или машин.

Дисциплина обслуживания – это совокупность правил поведения заявки в СМО от момента ее поступления в систему до момента прекращения обслуживания.

К основным правилам обслуживания относятся:

- выбор свободного прибора;

- дисциплина очереди;

- назначение очередной заявки на обслуживание.

Если к моменту поступления заявки имеется несколько свободных приборов, то должно быть задано правило, согласно которому определяется прибор для ее обслуживания. Выбор свободного прибора может осуществляться:

- случайным образом (например, с равной вероятностью);

- в порядке нумерации (наибольший или наименьший номер);

- в зависимости от времени нахождения прибора в состоянии «свободен» (наименьшее или наибольшее время).

Дисциплина очереди определяет, в каких случаях заявка становится в очередь (и в какую из очередей, если к каждому ОП в многоканальной СМО образуется своя очередь) и когда она покидает СМО. Задается дисциплина очереди в виде ограничений, накладываемых на параметры СМО. Чаще всего ограничения накладываются на длину очереди (максимально допустимое число заявок в очереди m), время ожидания заявки в очереди t_ож или время пребывания заявки в системе t_с.

Следует подчеркнуть, что дисциплина очереди не является чем-то внешним по отношению к заявкам. Наоборот, чаще всего ограничения, накладываемые на параметры системы, определяются характером заявок. Так, например, удар по подвижной цели должен быть подготовлен и нанесен за время, не превышающее время пребывания цели в определенном районе, т.е. время пребывания заявки в системе ограничено временем пребывания цели в заданном районе.

В общем случае ограничение на длину очереди заключается в том, что заявка, застав очередь длины k остается в ней с вероятностью P_k (или не присоединяется к очереди с вероятностью q_k=1-P_k). Указанные на рис. 2.2 СМО являются частными случаями. Действительно, для СМО с конечной очередью

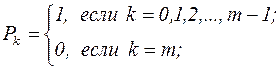(2.2)

для чистой СМО с ожиданием P_k= 1 для любого k.

В СМО с отказами очередь не образуется, так как заявка, заставшая все приборы занятыми, покидает систему (теряется). Однако в методическом плане эту систему целесообразно рассматривать как частный случай СМО с конечной очередью (m= 0).

Ограничение времени ожидания в очереди или времени пребывания в системе (так называют сумму времени ожидания времени обслуживания) означает, что заявка может ожидать обслуживания или находиться в СМО какое-то время, не превышающее некоторой случайной величины τ_ож или τ_{с .} Системы с ограничением на время ожидания (или пребывания) называют смешанными СМО. Система, в которой не накладывается ограничение ни на одну из величин m, t_с, и t_ож называется чистой СМО с ожиданием. Эту систему можно рассматривать как предельный случай, когда m→∞, t_c→∞, t_ож→∞.

Если входящий поток однородный, то в основе правил назначения очередной заявки лежит или фактическое время ожидания, или остающаяся часть времени ожидания (пребывания). Частными случаями являются:

- неупорядоченность – равновероятное поступление на обслуживание любой заявки из очереди;

- строгая очередность – заявки к обслуживанию назначаются в порядке поступления;

- обратная очередность – «последним пришел – первым обслуживается».

Иногда назначение на обслуживание происходит по некоторой системе приоритетов (Герои Советского Союза обслуживаются вне очереди).

Реальные процессы обслуживания не исчерпываются рассмотренными правилами. К числу возможных и встречающихся на практике правил относятся:

- зависимость допустимого времени ожидания (пребывания) от фактического времени ожидания (пребывания);

- зависимость времени обслуживания от длины очереди (например, с ростом очереди время обслуживания уменьшается);

- зависимость числа приборов от длины очереди (например, с
ростом очереди число приборов растет).

Из изложенного следует, что классификация, приведенная на рис. 2.2, не охватывает всего многообразия СМО и учитывает только наиболее важные, определяющие факторы.

Кроме рассмотренной классификации СМО по содержательным свойствам основных элементов их можно классифицировать по математическим методам исследования, которые определяются видом законов распределения интервалов времени между поступлениями заявок и времени обслуживания.

Рассмотрим наиболее важные виды законов распределения, используемых для описания входящего потока и потока обслуженных заявок.

3. Потоки событий, их свойства и математическое описание

Входящий и выходящий потоки СМО представляют собой последовательность однородных событий, следующих одно за другим в случайные моменты времени.

Вид закона распределения промежутков времени между соседними событиями определяется структурой и свойствами потока. Наиболее важными являются следующие свойства потоков: стационарность, ординарность и отсутствие последействия.

Стационарность потока означает, что его вероятностные характеристики не зависят от времени. Одной из важнейших характеристик потока является его интенсивность λ - среднее число событий в единицу времени. Очевидно, что 1 / λ - средняя длительность интервала между событиями (математическое ожидание).

Поэтому

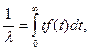(2.3)

где f(t) - плотность распределения длительностей интервалов между событиями. Для стационарного потока λ = const.

Ординарность потока означает практическую невозможность появления двух и более событий в один и тот же момент времен.

Отсутствие последствия означает, что события появляются в потоке независимо друг от друга, т.е. вероятность появления определенного числа событий за некоторый произвольно выбранный промежуток времени не зависит от того, сколько событий произошло раньше (не зависит от предыстории изучаемого потока). В этом случае длительность интервалов представляют независимые случайные величины. Если эти случайные величины имеют один и тот же закон распределения, то поток событий называется рекуррентным.

Поток событий, обладающий всеми тремя свойствами, называет простейшим. Для простейшего потока число событий, попадающих на любой участок, распределено по закону Пуассона, т.е. вероятность попадания на участок длительности τ ровно k событий

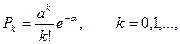(2.4)

где α = λτ - среднее число событий, приходящихся на участок τ.

Поэтому простейший поток часто называют стационарным пуассоновским потоком. Для нестационарного пуассоновского потока

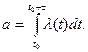
Определим закон распределения интервала времени 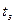между событиями в простейшем потоке:

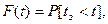
т.е. вероятность того, что 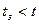. Эта вероятность равна вероятности того, что на участок времени t попадает хотя бы од­но событие, т.е.

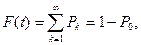
где 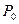- вероятность того, что на участок t не попадает ни одно событие. Учитывая выражение (2.4), получим

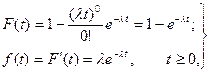(2.5)

т.е. закон распределение интервалов времени между событиями в простейшем потоке является экспоненциальным (показательным). Математическое ожидание 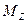, дисперсия 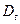и среднее квадратическое отклонение 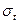определяются соотношениями

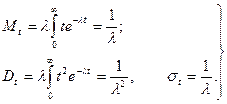(2.6)

Экспоненциальное распределение обладает замечательным свойством «не помнить о прошлом»: если рассматриваемый промежуток времени уже «длился» некоторое время, то это никак не влияет на закон распределения оставшейся части этого промежутка. Доказательство этого положения приведено в работе [2].

Рассмотрим пример. Пусть по улице проходят свободные такси со средним интервалом 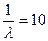мин. Предположим, что мы пыта­емся поймать такси с некоторого произвольного момента времени. Если интервалы времени между прохождениями такси распределены по показательному закону, то в среднем мы будем ожидать 10 мин, если эти интервалы постоянны, то в среднем пришлось бы ожидать в течение 5 мин.

Применительно к потоку заявок указанное свойство простейшего потока можно сформулировать так: вероятность поступления заявки в течение некоторого интервала времени не зависит от того, сколько времени прошло после поступления предыдущей заявки. Именно поэтому простейший поток иногда называют «совершенно случайным потоком».

Простейший поток заявок играет чрезвычайно важную роль в теории массового обслуживания. Можно доказать, что суммарный поток, образующийся при взаимном наложении достаточно большого числа потоков, обладающих последствием, является простейшим, если все составляющие потоки стационарны и ординарны. Достаточные условия, при которых суммарный поток является простейшим, были найдены советским ученым А.Я. Хинчиным. Позднее его ученик Г.А. Осокин доказал, что эти условия являются и необходимыми. Очевидно, что поток, образованный суммой простейших потоков и интенсивности 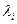, есть простейший поток интенсивности

.

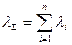Дата добавления: 2014-01-13