Определители и их свойства. Миноры и алгебраические дополнения

Курс лекций

О.В. Прохорова

СУБД Access

Access - это система управления базами данных (СУБД). Под системой управления понимается комплекс программ, который позволяет не только хранить большие массивы данных в определенном формате, но и обрабатывать их, представляя в удобном для пользователей виде. Access дает возможность также автоматизировать часто выполняемые операции (например, расчет заработной платы, учет материальных ценностей и т.п.). С помощью Access можно не только разрабатывать удобные формы ввода и просмотра данных, но и составлять сложные отчеты.

Введение в линейную алгебру

Оглавление

1. Определители и их свойства. Миноры и алгебраические дополнения. 3

2. Матрицы. Действия над матрицами. Понятие ранга матрицы. 17

3. Системы линейных уравнений. Их решение. 31

4. Матричная запись системы. Метод Гаусса. Метод Крамера. 36

5. Элементы векторной алгебры. Линейные операции над векторами.. 56

6. Скалярное, векторное, смешанное произведение векторов. Свойства. 62

7. Линейные пространства и операции над ними. 75

8. Размерность и базис линейного пространства. Линейные операции.. 84

9. Подпространства линейного пространства. Евклидово пространство. 91

Литература. 111

Аннотация: В этом разделе рассказывается о системах линейных уравнений со многими неизвестными и постоянными коэффициентами и некоторых базовых способах поиска решения.

Определители второго порядка и их свойства

На практике часто исследователю приходится иметь дело с неизвестными величинами, связанными между собой некоторыми заранее определенными зависимостями, которые могут быть выражены любыми формулами. Если при этом выполняется ряд условий:

1. коэффициенты в формулах постоянные,

2. неизвестные входят в формулы только в первой степени,

3. отсутствуют произведения между самими неизвестными,

то тогда такие зависимости называют линейными.

Пример. В лаборатории 10 образцов имеют общий вес 280 г. Найти средний вес одного образца, если тара весит 15 г.

Решение. Для ответа на вопрос воспользуемся простым уравнением:

10 x+15=280,

обозначив за x средний вес одного образца. Решением составленного уравнения будет 26,5 г.

В примере мы имели дело с линейными зависимостями– с линейным уравнением.

Если взять систему уравнений вида:

10x+10y=280;

5x+2y=128,

и заменим коэффициенты буквами и получим линейную систему уравнений:

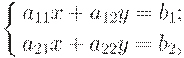
(1.1)

где a₁₁, a₁₂, a₂₁, a₂₂, b₁, b₂, - некоторые числа, x, y - неизвестные. Составим из коэффициентов системы (1.1) прямоугольную таблицу вида

(1.2)

Определение. Матрицей будем называть любую прямоугольную таблицу, составленную из чисел a_ij.

Определение. Элементы a_ij, из которых составлена матрица, называют элементами данной матрицы.

Определение. Определителем второго порядка или детерминантом, соответствующим матрице(1.2) назовем число D такое, что

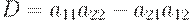
(1.3)

Определитель обозначается буквами D или и записывается

Следует обратить внимание, что хотя определитель есть число, по определению, но он записывается в виде таблицы. Тогда можно сказать, например, о перестановке строк или столбцов в этой таблице. В таком случае следует говорить "определитель, соответствующий матрице". Но на практике обычно вторая часть этой фразы для простоты опускается и тогда остается только одно слово – определитель. Для того, чтобы различить, что имеется в виду – сам определитель в виде таблицы или его найденное значение, во втором случае используют слово детерминант. Поэтому, если говорят, например, "количество строк в определителе…", то имеют в виду определитель, соответствующий матрице, но еще не вычисленный до единственного числа. А, если говорят детерминант, то имеют в виду, что данный определитель представлен единственным числом, вычисленным по формуле.

Пример. Дана система уравнений

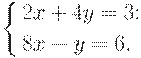
Составить матрицу системы и вычислить определитель.

Решение. Из коэффициентов системы составим матрицу:

и соответствующий ей детерминант

Выполним вычисления по формуле (1.2), получим

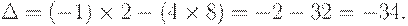
Определение. Количество строк (или столбцов) в определителе называется порядком определителя.

В примере был вычислен определитель второго порядка.

Определители обладают следующими свойствами:

1. Определитель не изменится, если его строки заменить столбцами и наоборот.

Покажем это. Пусть дан определитель второго порядка

Заменим строки столбцами и снова вычислим получившийся определитель

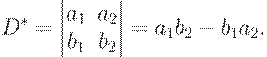
Сравнивая D с D^*можно убедиться, что D = D^*.

Определение. Операция замены строк столбцами (или наоборот) в определителе называется транспонированием.

2. При перестановке двух строк или столбцов определитель меняет свой знак.

Поверку этого свойства проведем на примере. Пусть дан определитель

Поменяем в нем местами столбцы и вычислим получившийся определитель.

Сравнивая результаты, убеждаемся, что определитель, действительно, поменял свой знак. Поменяем теперь местами строки и вновь убедимся в справедливости данного свойства.

Заметим, что все остальные приводимые здесь свойства доказываются аналогично на примерах, очень просто и поэтому далее все свойства приводятся без доказательств. Читатель может в качестве упражнений самостоятельно проверить каждое из этих свойств.

3. Если все элементы какого-либо столбца (или строки) матрицы умножить (или разделить) на одно и то же число m, отличное от нуля, то определитель также умножится (разделится) на это число.

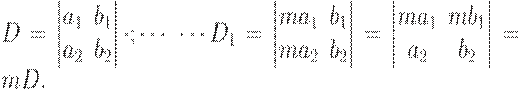
4. Определитель, у которого элементы одной строки (столбца) пропорциональны другой строке (столбцу), равен нулю.

5. Если каждый элемент какой-либо строки (столбца) можно представить как сумму двух слагаемых, то определитель будет равен сумме двух определителей. У первого из слагаемых определителей элементами соответствующей строки (столбца) будет первое слагаемое, а у другого - второе. Остальные элементы этих определителей будут такие же, как у исходного.

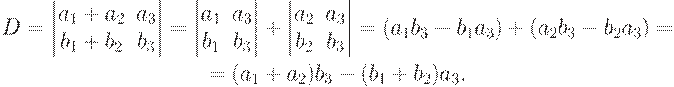
Сравнивая результат с исходным определителем убеждаемся в справедливости свойства.

Это свойство широко используется для практических вычислений при работе с определителями порядка больше трех.

6. Определитель не изменится, если к элементам какого-либо столбца (строки) прибавить соответствующие элементы другого столбца (строки), предварительно умноженные на какое-либо число.

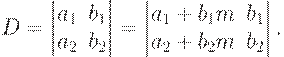
Определитель - очень удобная математическая форма, которая позволяет быстро находить решение систем линейных уравнений. Большинство задач, связанных с вычислительной математикой, используют математический аппарат теории определителей.

Определители третьего порядка и их свойства

На практике редко задачи решаются при помощи таких простых систем, как рассмотренные в первом параграфе. Чаще для поиска решения получаются системы, состоящие из большего количества уравнений. Да и неизвестных в таких системах тоже больше, чем два. Пусть теперь дана система из трех линейных уравнений относительно трех неизвестных

(1.4)

Определение. Определителем третьего порядка, соответствующим матрице системы (1.4), назовем число D, равное

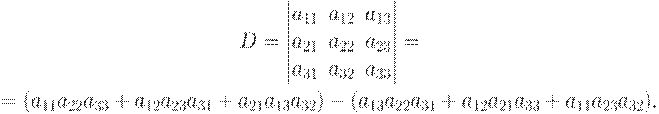
Для того, чтобы вычислить определитель третьего порядка применяют две вычислительные схемы, позволяющие вычислять определители третьего порядка без особых хлопот. Эти схемы известны как " правило треугольника " (или "правило звездочки") и " правило Саррюса ".

По правилу треугольника сначала перемножаются и складываются элементы, соединенными на схеме линиями

т.е. получаем сумму произведений: a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₂₁a₁₃a₃₂.

Обратите внимание, что перемножаются элементы, соединенные одной линией, прямой или ломанной, а потом полученные произведения складываются.

Затем перемножаются и складываются элементы, соединенные на схеме

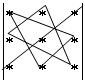
т.е. получаем другую сумму произведений a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂. И, наконец, чтобы вычислить определитель, из первой суммы вычитают вторую. Тогда окончательно получаем формулу вычисления определителя третьего порядка:

D = (a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₂₁a₁₃a₃₂)-(a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂).

По правилу Саррюса к определителю справа дописывают два первых столбца, а затем считают сумму произведений элементов определителя в одном направлении и из нее вычитают сумму произведений элементов в другом направлении (см. схему):

Можно убедиться, что результат будет таким же, что и при вычислении определителя по правилу треугольника.

Заметим, что все свойства, сформулированные для определителей второго порядка, справедливы для определителей третьего порядка, в чем можно убедиться самостоятельно. На основании этих свойств сформулируем общие свойства для определителей любого порядка:

· Величина определителя не изменяется при замене строк столбцами.

· При перестановке двух строк (столбцов) между собой, величина определителя меняет знак.

· Определитель с двумя одинаковыми (пропорциональными) строками (столбцами) равен нулю.

· Если все элементы некоторой строки (столбца) содержат одинаковый множитель, то этот множитель можно вынести за знак определителя.

· Если все элементы некоторой строки (столбца) есть сумма равного числа слагаемых, то определитель будет равен сумме определителей, в которых элементы указанной строки (столбца) записываются отдельными слагаемыми.

· Если все элементы некоторой строки (столбца) равны нулю, то весь определитель тоже равен нулю.

· Величина определителя не изменится, если к элементам некоторой строки (столбца) добавить соответствующие элементы другой строки (столбца), предварительно умножив их на один и тот же множитель.

Дата добавления: 2014-01-13