Локальная форма закона сохранения массы

(уравнение неразрывности)

В локальной форме закон сохранения массы может быть сформулирован аналогично материальному балансу. Отличие заключается лишь в том, что в данном случае рассматривается не конечный объем V, а бесконечно малый dV. Получим математическую формулировку закона в такой форме. Отметим, что речь идет не о выводе закона, а получении одного из вариантов его математической записи.

Рассмотрим движение среды как целого через элементарный фиксированный объем dV = dxdydz. При прохождении через данный объем возможно изменение массового потока 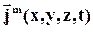, обусловленное изменением скорости 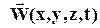и плотности r(x,y,z,t) среды.

Рис.2. Изменение массового потока, направленного вдоль оси х, проходящего через элементарный объем dV

Массовый расход среды, входящий в объем dV через грань, перпендикулярную оси x будет равен

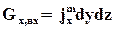(25)

а выходящий можно представить как

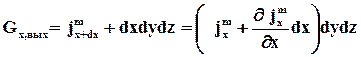(26)

Изменение расхода вдоль оси x:

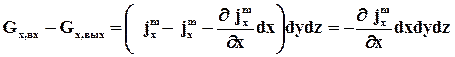(27)

Аналогичным образом можно рассмотреть изменения массового расхода вдоль осей y и z.

Суммарное изменение расхода в объеме dV равно сумме изменений по всем трем осям:

(28)

Применим к рассматриваемому объему dV уравнение материального баланса (20), используя в нем частную производную от плотности по времени с учетом того, что плотность зависит еще и от пространственных координат

(29)

Решая совместно уравнения (28) и (29), получим

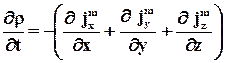(30)

Используя дифференциальный оператор 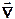, а также выражение для потока массы, эту запись можно представить в виде

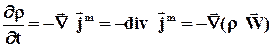(31)

Данное уравнение, выражающее в локальной форме закон сохранения массы, носит название уравнения неразрывности. Левая часть этого уравнения характеризует изменение во времени плотности движущейся среды в фиксированной точке пространства (элементарном объеме dV). Зачастую интерес представляет изменение плотности во времени в точке, движущейся вместе с потоком, т.е. со скоростью 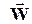. Для этого необходимо использовать полную производную по времени

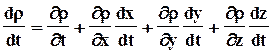(32)

Учитывая, что производные от пространственных координат по времени дают соответствующие проекции вектора скорости можно переписать

(33)

Такая полная производная по времени от величин, зависящих также от пространственных координат, носит название субстанциональной производной, обозначается Dr/Dt и характеризует изменение величины во времени для наблюдателя, движущегося вместе с потоком со скоростью 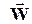. Рассмотрим частный случай установившегося (стационарного) движения, при этом в каждой точке пространства, фиксированной относительно лабораторной системы отсчета, плотность со временем меняться не будет (¶r¤¶t = 0). Однако, плотность может меняться в пространстве, тогда для движущегося вместе с потоком наблюдателя она со временем будет изменяться (dr/dt ¹0) по (33). Первый член этого уравнения характеризует локальное изменение величины, а последующие три - конвективное.

Уравнение неразрывности можно записать с использованием субстанциональной производной. Распишем правую часть уравнения (31) как производную от произведения двух функций и перенесем конвективный член в левую часть

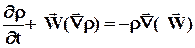(34)

Левая часть уравнения (34) есть в соответствии с (33) субстанциональная производная, тогда

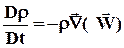(35)

Рассмотрим частные случаи уравнения неразрывности. В случае установившегося (стационарного) движения ¶r¤¶t = 0 и из (31) следует

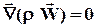(36)

В случае постоянства плотности среды Dr/Dt = 0 из (35) следует

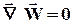(37)

Проинтегрировав уравнение (36), либо на основании (20) можно получить уравнение постоянства расхода, применимое для установившегося движения среды полностью заполняющей сечение канала S

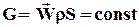(38)

Выше было рассмотрено движение среды в целом. Для многокомпонентных систем нетрудно получить закон сохранения массы в локальной форме для каждого компонента

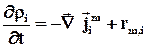(39)

В общем случае закон сохранения массы применительно к единичному объему можно сформулировать следующим образом

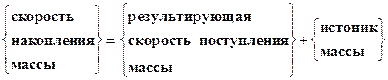
Для потока вещества, поделив уравнение (39) на мольную массу компонента m_i, получим

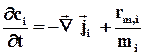(40)

Рассмотрим наиболее простой случай массопереноса в двухкомпонентной среде при отсутствии химических реакций. Можно записать уравнение нестационарной конвективной диффузии

(41)

Используя допущение о постоянстве r и, учитывая, что при этом 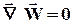по (37), получим

(42)

В случае 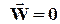Þ D_т = 0, Dc_i/Dt=¶c_i/¶t, и допустив ^m D _ij = const, получим уравнение, называемое вторым законом Фика

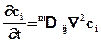(43)

Если предположить при этом стационарность процесса, то оно упростится еще более

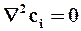(44)

Таким образом, на основе закона сохранения и уравнения переноса массы получены дифференциальные уравнения, решив которые можно определить поля концентраций и массовых потоков компонентов в любом аппарате. Интегрирование дифференциальных уравнений дает общее решение, справедливое для класса процессов. Для получения конкретного частного решения необходимо дополнить уравнение условиями однозначности.

Дата добавления: 2014-01-13