Изображение синусоидально изменяющихся величин векторами на комплексной плоскости

Комплексный (символический) метод расчета цепей переменного тока

Расчет сложных цепей можно выполнить путем отыскания частных случаев решений неоднородных дифференциальных уравнений, записанных на основе законов Кирхгофа.

Однако такой путь является громоздким и требует большой затраты времени. Громоздкость подобных вычислений является следствием того, что синусоидальная величина – ток, напряжение, ЭДС – при заданной частоте w определяется двумя величинами: амплитудой и начальной фазой.

Существенное упрощение достигается изображением синусоидальных функций времени комплексными числами (рис3). Для этой цели в электротехнике был разработан так называемый комплексный (символический) метод расчета цепей переменного тока, основанный также на законах Кирхгофа, но отличающийся значительной простотой при практическом использовании.

Сущность комплексного метода заключается в замене синусоидальных функций времени векторами, расположенными на комплексной плоскости. Такая замена позволяет применить к решению задач электротехники хорошо разработанный аппарат алгебры комплексных чисел. Действия над комплексными числами выполняются значительно проще, быстрее, чем действия над исходными тригонометрическими функциями. После выполнения всех расчетов путем обратного перехода можно, в случае необходимости, вернуться к исходным (синусоидальным величинам) времени.

Метод применим только к тем цепям, в которых все синусоидальные величины изменяются с одной и той же частотой.

При расчете режима работы цепи синусоидального тока комплексным методом полезно выделить несколько логически самостоятельных этапов:

1) представить исходные данные о параметрах всех элементов цепи в комплексной форме. Это означает, что, во-первых, синусоидальные ЭДС источников напряжения или токи, заданные мгновенными значениями (в тригонометрической форме), следует представить комплексными значениями и, во-вторых, для индуктивных и емкостных элементов цепи нужно определить соответствующие комплексные сопротивления или комплексные проводимости;

2) выбрать положительные направления для токов во всех ветвях,
указав их стрелками на схеме замещения;

3) пользуясь законами Ома и Кирхгофа в комплексной форме и учитывая выбранные положительные направления токов в ветвях, составить систему уравнений, определяющую режим работы цепи;

4) решить полученную систему уравнений, то есть определить комплексные значения токов в ветвях цепи и комплексные значения напряжений на ее элементах.

Найденные комплексные значения токов и напряжений однозначно определяют соответствующие им мгновенные значения синусоидальных, токов и напряжений.

Изображение синусоидальных функций (напряжения, тока и т.п.)

С помощью вращающихся векторов можно показать синусоидальные величины, что позволяет дать наглядное представление о фазовых и амплитудных соотношениях в цепи переменного тока.

Для изображения тока I = I_m sin (wt +y_i ) в виде вращающегося вектора возьмем вектор ОВ (рис.3), равный по модулю амплитуде тока I_m, и расположим его под углом y_i к линии 0х. Условимся отсчитывать положительные углы от оси 0х против часовой стрелки.

Тогда проекция вектора ОВ на вертикальную ось 0у равна мгновенному значению тока для момента времени t = 0. Для получения мгновенного значения тока в какой-либо другой момент времени, например t₁, нужно повернуть вектор ОВ на угол wt₁ против часовой стрелки и взять проекцию 0В на вертикальную ось 0у. Эта проекция i_t1 равно мгновенному значению тока в момент t = t₁:

i_t = I_m sin (wt₁ + y_i).

В заключении подчеркнем, что вращающиеся векторы являются математическими векторами в отличие от физических векторов.

Пусть имеем:

(1)

Эти синусоидальные величины (функции) могут быть изображены вращающимися векторами на комплексной плоскости.

В свою очередь любое комплексное число на комплексной плоскости изображается вектором, длина которого характеризует модуль комплексного числа, а угол наклона вектора к вещественной оси представляет собой аргумент комплексного числа (рис. 4).

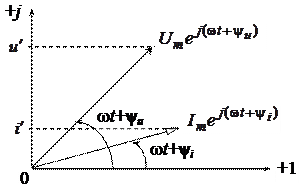Рис. 4

Т.к. комплексное число может быть представлено в показательной, тригонометрической и алгебраической формах, то:

(2)

Первые слагаемые в выражении (2) – действительные части комплексных чисел, т.е.

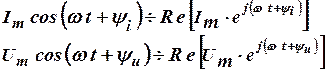
а вторые – коэффициенты при мнимой части:

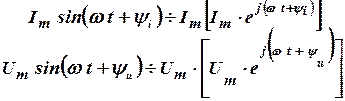
А так как в соответствии с (1)

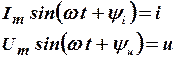
то синусоидально изменяющийся ток и напряжение можно представить, как проекцию вращающегося вектора на мнимую ось j.

Комплексное число удобно представить в форме:

(3)

где

(4)

называются комплексными амплитудами тока и напряжения. Они изображают ток и напряжение на комплексной плоскости для момента времени .

Число 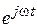называют оператором поворота.

Комплексные амплитуды обозначают заглавными буквами с индексами m и точкой над заглавными буквами.

Комплексные амплитуды неподвижны, они не вращаются и не являются функциями времени.

На комплексной плоскости они изображаются векторами рис. 5, а.

а) б)

Рис. 5

Если в уравнениях (4) левую и правую часть поделить на 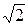, получим значения комплексных действующих токов и напряжений (комплексных токов и напряжений), определяемых уравнениями (5)

(5)

На комплексной плоскости они изображаются соответствующими векторами (рис. 5, б).

Дата добавления: 2014-01-13