Сортировка с помощью дерева (Heapsort)

Начнем с простого метода сортировки с помощью дерева, при использовании которого явно строится двоичное дерево сравнения ключей. Построение дерева начинается с листьев, которые содержат все элементы массива. Из каждой соседней пары выбирается наименьший элемент, и эти элементы образуют следующий (ближе к корню уровень дерева). Из каждой соседней пары выбирается наименьший элемент и т.д., пока не будет построен корень, содержащий наименьший элемент массива. Двоичное дерево сравнения для массива, используемого в наших примерах, показано на рисунке 2.1. Итак, мы уже имеем наименьшее значение элементов массива. Для того, чтобы получить следующий по величине элемент, спустимся от корня по пути, ведущему к листу с наименьшим значением. В этой листовой вершине проставляется фиктивный ключ с "бесконечно большим" значением, а во все промежуточные узлы, занимавшиеся наименьшим элементом, заносится наименьшее значение из узлов - непосредственных потомков (рис. 2.2). Процесс продолжается до тех пор, пока все узлы дерева не будут заполнены фиктивными ключами (рисунки 2.3 - 2.8).

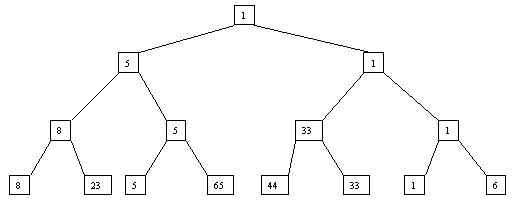
Рис. 2.1.

Рис. 2.2. Второй шаг

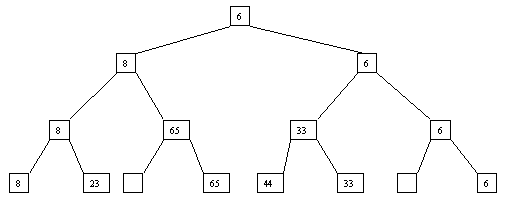
Рис. 2.3. Третий шаг

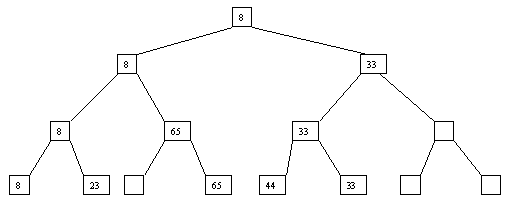
Рис. 2.4. четвертый шаг

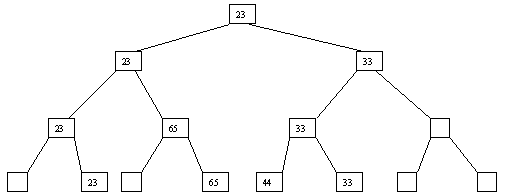
Рис. 2.5. Пятый шаг

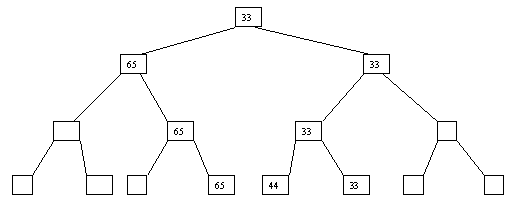
Рис. 2.6. Шестой шаг

Рис. 2.7. Седьмой шаг

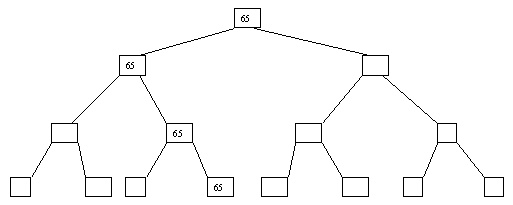
Рис. 2.8. Восьмой шаг

На каждом из n шагов, требуемых для сортировки массива, нужно log n (двоичный) сравнений. Следовательно, всего потребуется n log n сравнений, но для представления дерева понадобится 2n - 1 дополнительных единиц памяти.

Имеется более совершенный алгоритм, который принято называть пирамидальной сортировкой (Heapsort). Его идея состоит в том, что вместо полного дерева сравнения исходный массив a[1], a[2],..., a[n] преобразуется в пирамиду, обладающую тем свойством, что для каждого a[i] выполняются условия a[i] <= a[2i] и a[i] <= a[2i+1]. Затем пирамида используется для сортировки.

Наиболее наглядно метод построения пирамиды выглядит при древовидном представлении массива, показанном на рисунке 2.9. Массив представляется в виде двоичного дерева, корень которого соответствует элементу массива a[1]. На втором ярусе находятся элементы a[2] и a[3]. На третьем - a[4], a[5], a[6], a[7] и т.д. Как видно, для массива с нечетным количеством элементов соответствующее дерево будет сбалансированным, а для массива с четным количеством элементов n элемент a[n] будет единственным (самым левым) листом "почти" сбалансированного дерева.

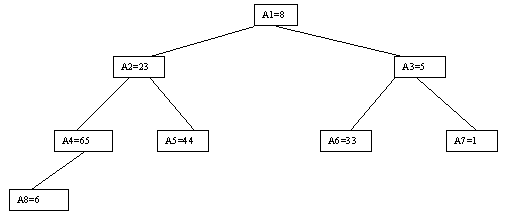
Рис. 2.9.

Очевидно, что при построении пирамиды нас будут интересовать элементы a[n/2], a[n/2-1],..., a[1] для массивов с четным числом элементов и элементы a[(n-1)/2], a[(n-1)/2-1],..., a[1] для массивов с нечетным числом элементов (поскольку только для таких элементов существенны ограничения пирамиды). Пусть i - наибольший индекс из числа индексов элементов, для которых существенны ограничения пирамиды. Тогда берется элемент a[i] в построенном дереве и для него выполняется процедура просеивания, состоящая в том, что выбирается ветвь дерева, соответствующая min(a[2*i], a[2*i+1]), и значение a[i] меняется местами со значением соответствующего элемента. Если этот элемент не является листом дерева, для него выполняется аналогичная процедура и т.д. Такие действия выполняются последовательно для a[i], a[i-1],..., a[1]. Легко видеть, что в результате мы получим древовидное представление пирамиды для исходного массива (последовательность шагов для используемого в наших примерах массива показана на рисунках 2.10-2.13).

Рис. 2.10.

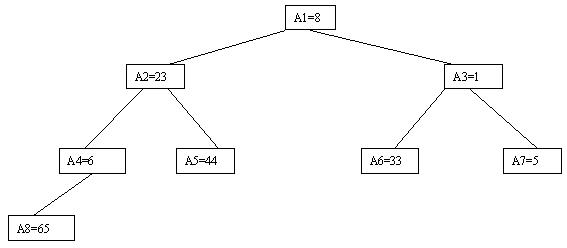
Рис. 2.11.

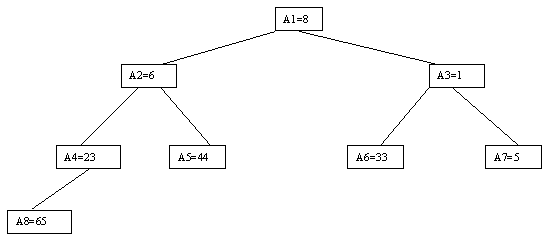
Рис. 2.12.

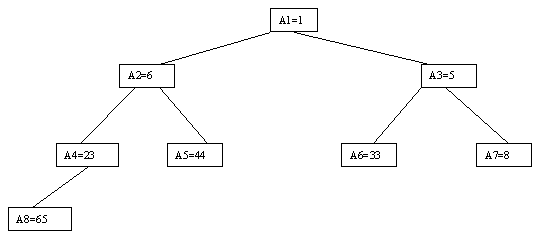
Рис. 2.13.

В 1964 г. Флойд предложил метод построения пирамиды без явного построения дерева (хотя метод основан на тех же идеях). Построение пирамиды методом Флойда для нашего стандартного массива показано в таблице 2.7.

Таблица 2.7 Пример построения пирамиды

Начальное состояние массива	8 23 5 |65| 44 33 1 6
Шаг 1	8 23 |5| 6 44 33 1 65
Шаг 2	8 |23| 1 6 44 33 5 65
Шаг 3	|8| 6 1 23 44 33 5 65
Шаг 4	1 6 8 23 44 33 5 651 6 5 23 44 33 8 65

В таблице 2.8 показано, как производится сортировка с использованием построенной пирамиды. Суть алгоритма заключается в следующем. Пусть i - наибольший индекс массива, для которого существенны условия пирамиды. Тогда начиная с a[1] до a[i] выполняются следующие действия. На каждом шаге выбирается последний элемент пирамиды (в нашем случае первым будет выбран элемент a[8]). Его значение меняется со значением a[1], после чего для a[1] выполняется просеивание. При этом на каждом шаге число элементов в пирамиде уменьшается на 1 (после первого шага в качестве элементов пирамиды рассматриваются a[1], a[2],..., a[n-1]; после второго - a[1], a[2],..., a[n-2] и т.д., пока в пирамиде не останется один элемент). Легко видеть (это иллюстрируется в таблице 2.8), что в результате мы получим массив, упорядоченный в порядке убывания. Можно модифицировать метод построения пирамиды и сортировки, чтобы получить упорядочение в порядке возрастания, если изменить условие пирамиды на a[i] >= a[2*i] и a[1] >= a[2*i+1] для всех осмысленных значений индекса i.

Таблица 2.8 Сортировка с помощью пирамиды

Исходная пирамида	1 6 5 23 44 33 8 65
Шаг 1	65 6 5 23 44 33 8 15 6 65 23 44 33 8 15 6 8 23 44 33 65 1
Шаг 2	65 6 8 23 44 33 5 16 65 8 23 44 33 5 16 23 8 65 44 33 5 1
Шаг 3	33 23 8 65 44 6 5 18 23 33 65 44 6 5 1
Шаг 4	44 23 33 65 8 6 5 123 44 33 65 8 6 5 1
Шаг 5	65 44 33 23 8 6 5 133 44 65 23 8 6 5 1
Шаг 6	65 44 33 23 8 6 5 144 65 33 23 8 6 5 1
Шаг 7	65 44 33 23 8 6 5 1

Процедура сортировки с использованием пирамиды требует выполнения порядка n*log n шагов (логарифм - двоичный) в худшем случае, что делает ее особо привлекательной для сортировки больших массивов.

{процедура просеивания Флойда in situ}

PROCEDURE sito(l,r:byte);

VAR

i,j: BYTE;

x: INTEGER;

BEGIN

i:=l; j:=2*i; x:=a[i];

IF (j<r) AND (a[j+1]<a[j]) THEN j:=j+1;

WHILE (j<=r) AND (a[j]<x) DO BEGIN

a[i]:=a[j]; i:=j; j:=2*j;

IF (j<r) AND (a[j+1]<a[j]) THEN j:=j+1;

END;

a[i]:=x

END;

….

BEGIN

….

{построение пирамиды}

l:=(n DIV 2)+1;

WHILE l>1 DO BEGIN

l:=l-1; sito(l,n);

END;

….

{полная сортировка}

r:=n;

WHILE r>1 DO BEGIN

x:=a[1]; a[1]:=a[r]; a[r]:=x;

r:=r-1; sito(1,r);

END;

Анализ Heapsort. На первый взгляд вовсе не очевидно, что такой метод сортировки дает хорошие ре­зультаты. Ведь в конце концов большие элементы, прежде чем попадут на свое место в правой части, сначала сдвигаются влево. И действительно, про­цедуру не рекомендуется применять для небольшого, вроде нашего примера, числа элементов. Для боль­ших же n Heapsort очень эффективна; чем больше n, тем лучше она работает. Она даже становится срав­нимой с сортировкой Шелла.

В худшем случае нужно n/2 сдвигающих шагов, они сдвигают элементы на log (n/2), log (n/2 - 1),......, log(n - l) позиций (логарифм (по основанию 2) «обрубается» до следующего меньшего целого). Сле­довательно, фаза сортировки требует n - 1 сдвигов с самое большое log(n - l), log (n -),..., 1 перемещениями. Кроме того, нужно еще n - 1 перемещений для просачивания сдвинутого элемента на некоторое расстояние вправо. Эти соображения показывают, что даже в самом плохом из возможных случаев Heapsort потребует n * log n шагов. Великолепная произ­водительность в таких плохих случаях—одно из при­влекательных свойств Heapsort.

Совсем не ясно, когда следует ожидать наихудшей (или наилучшей) производительности. Но вообще-то кажется, что Heapsort «любит» начальные последо­вательности, в которых элементы более или менее отсортированы в обратном порядке. Поэтому ее по­ведение несколько неестественно. Если мы имеем дело с обратным порядком, то фаза порождения пирамиды не требует каких-либо перемещений. Среднее число перемещений приблизительно равно n/2*log(n), при­чем отклонения от этого значения относительно неве­лики.

Дата добавления: 2014-01-13