
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение прямоугольных координат
|
|
|
|
В каждой координатной зоне строится координатная сетка (рис. 13).
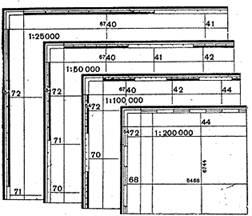
Рис. 13. Координатная сетка на топографических картах разных масштабов
Она представляет собой сетку квадратов, образованных линиями, параллельными координатным осям зоны. Линии сетки проводятся через целое число километров. Поэтому координатную сетку называют также километровой сеткой, а ее линии - километровыми. Если изображение одной зоны с нанесенной на ней сеткой квадратов разделить на отдельные листы карты, то каждый лист будет покрыт координатной сеткой, составляющей часть разграфки, общей для всей зоны.
Координатная сетка используется для определения прямоугольных координат точек, отыскания на карте местоположения различных объектов при докладах, постановке задач, составлении донесений, для быстрой глазомерной оценки расстояний, площадей, определения направлений и ориентирования карты.
Километровые линии, ближайшие к углам рамки листа карты, подписываются полным числом километров, остальные — сокращенно, последними двумя цифрами. Таким образом, подпись 6062 (рис. 14) у крайней снизу горизонтальной линии означает, что эта линия проходит в 6062 км к северу от экватора. Подпись 6394 у крайней слева вертикальной километровой линии означает, что она находится в шестой зоне и проходит в 394 км от начала счета ординат, т. е. на 106 км западнее осевого меридиана зоны.
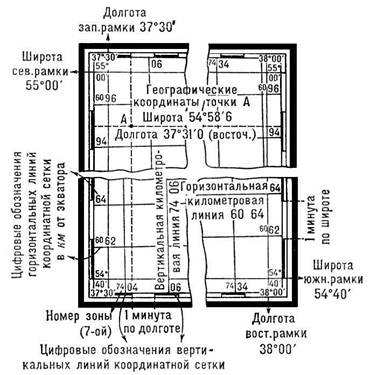
Рис. 14. Шкалы географических координат и километровая сетка
Чтобы указать приближенное местоположение какого-либо пункта на карте, достаточно назвать квадрат сетки, в котором он расположен. Для этого сначала читают (называют) оцифровку горизонтальной километровой линии, образующей южную сторону квадрата, а затем вертикальной линии, образующей его западную сторону, т. е. сначала абсциссу, а затем ординату юго-западного угла квадрата.
|
|
|
Например, при указании положения высоты 347,1 (рис. 12) следует сказать: «Квадрат десять, четырнадцать высота 347,1». В письменной же форме это будет выглядеть так «Высота 347,1 (1014)».
Для более точного указания положения какой-либо точки определяют ее координаты. Для этого к координатам южной и западной линий квадрата, в котором она находится, добавляют расстояния до определяемой точки от этих линий, записывая отдельно абсциссу Хи ординату Уточки.
Определяя, например, координаты точки А(рис. 15), сначала записывают абсциссу нижней километровой линии квадрата, в котором находится эта точка (т.е. 78). Затем измеряют по масштабу расстояние (по перпендикуляру) от точки Адо этой километровой линии, т.е. отрезок т, и полученную величину (1,225 км) добавляют к абсциссе линии. Так получается абсцисса Хточки А.
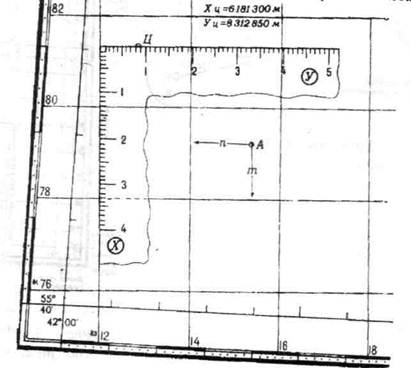
Рис. 15. Определение по карте прямоугольных координат точки А и нанесение цели (Ц) на карту по координатам (с помощью офицерской линейки)
Для получения ординаты Уточки записывают ординату левой (вертикальной) стороны того же квадрата (т.е. 14) и затем добавляют к ней расстояние, измеренное по перпендикуляру от определяемой точки до этой линии, т. е. отрезок п (в нашем примере 1,365 км).
Таким образом, координаты точки Абудут Х= 79 225 м; У= 15365 м. Так как в данном случае при определении координат точки цифровое обозначение километровых линий было записано не полностью, а лишь последними двумя цифрами (78 и 14), то такие координаты называют сокращенными координатами точки А.
Если же оцифровку километровых линий записывать полностью, то получим полные координаты. Для точки А:
Х = 6179225 м; У = 8315 365 м.
Если сокращенные подписи километровых линий на данном участке карты не повторяются, а потому положение объектов на нем определяется однозначно, то пользуются сокращенными координатами. В противном случае применяются полные координаты.
|
|
|
При определении координат точек по карте и нанесении точек на карту по координатам измерения выполняют циркулем или линейкой с миллиметровыми делениями. Для этой цели могут применяться также специальные координатомеры, которые несколько упрощают работу, заменяя циркуль и масштабную линейку.
Простейшим координатомером служит также офицерская линейка, на двух взаимно перпендикулярных краях которой, разбитых на миллиметровые деления, имеются подписи «Х» и «У». Пользование офицерской линейкой для нанесения на карту точки Ц по ее координатам показано на рис. 15.
Таким образом, из вышеизложенного можно сделать следующие основные выводы:
- система плоских прямоугольных координат является зональной. О номере координатной зоны Гаусса, в которой расположена точка, говорят начальные цифры ее полной координаты У, остающиеся после «отбрасывания» шести цифр справа. Например, точка, имеющая полную координату У=12600300, находится в двенадцатой координатной зоне, а точка с координатой У=635720 – в шестой координатной зоне;
- для определения координат целей и выдачи целеуказания на крупномасштабных картах пользуются, как правило, сокращенными прямоугольными координатами;
- точность определения прямоугольных координат зависит от точности измерения расстояний между данной точкой и ближайшими к ней километровыми линиями.
|
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 2039; Нарушение авторских прав?; Мы поможем в написании вашей работы!