Введение. Примеры итерационных методов решения нелинейных уравнений

Примеры итерационных методов решения нелинейных уравнений

Решение нелинейных уравнений и систем уравнений

Пусть задана функция 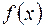действительного переменного. Требуется найти корни уравнения

(4.1)

или, что то же самое, нули функции .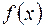

Уже на примере алгебраического многочлена известно, что нули 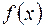могут быть как действительными, так и комплексными. Поэтому более точная постановка задачи состоит в нахождении корней уравнения (4.1), расположенных в заданной области комплексной плоскости. Можно также рассматривать задачу нахождения действительных корней, расположенных на заданном отрезке.

Задача нахождения корней уравнения (4.1) обычно решается в два этапа. На первом этапе изучается расположение корней (в общем случае на комплексной плоскости) и проводится их разделение, т.е. выделяются области в комплексной плоскости, содержащие только один корень. Кроме того, изучается вопрос о кратности корней. Тем самым находятся некоторые начальные приближения для корней уравнения (4.1). На втором этапе, используя заданное начальное приближение, строится итерационный процесс, позволяющий уточнить значение отыскиваемого корня.

Не существует каких-либо общих регулярных приемов решения задачи о расположении корней произвольной функции 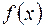. Наиболее полно изучен вопрос о расположении корней алгебраических многочленов

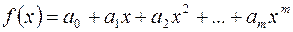. (4.2)

Численные методы решения нелинейных уравнений являются, как правило, итерационными методами, которые предполагают задание достаточно близких к искомому решению начальных данных.

Прежде чем переходить к изложению конкретных итерационных методов, отметим два простых приема определения действительных корней уравнения (4.1). Предположим, что 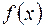определена и непрерывна на .

Первый прием состоит в том, что вычисляется таблица значений функции 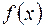в заданных точках 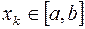, . Если обнаружится, что при некоторых числа 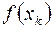, 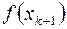имеют разные знаки, то это будет означать, что на интервале 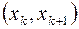уравнение (4.1) имеет, по крайней мере, один действительный корень (точнее имеет нечетное число действительных корней). Затем можно разбить интервал 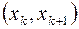на более мелкие интервалы и с помощью аналогичной процедуры уточнить расположение корня.

Более регулярным способом отделения действительных корней является метод бисекции (деления пополам). Предположим, что на 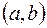расположен лишь один корень 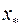уравнения (4.1). Тогда 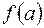и 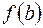имеют различные знаки. Пусть для определенности , 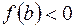. Положим 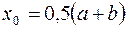и вычислим . Если 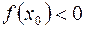, то искомый корень находится на интервале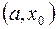. Если же 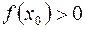, то 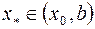. Далее из двух интервалов 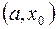и 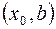выбираем тот, на границах которого функция 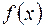имеет различные знаки, находим точку 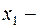середину выбранного интервала, вычисляем 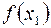и повторяем указанный процесс. В результате получаем последовательность интервалов, содержащих искомый корень 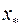, причем длина каждого последующего интервала вдвое меньше предыдущего. Процесс заканчивается, когда длина вновь полученного интервала станет меньше заданного числа , и в качестве 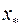приближенно принимается середина этого интервала.

Если на имеется несколько корней, то указанный процесс сойдется к одному из корней, но заранее неизвестно, к какому именно. Можно использовать прием выделения корней: если корень 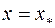кратности 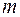найден, то рассматривается функция 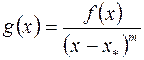и для нее повторяется процесс нахождения корня.

Дата добавления: 2014-01-13