Законы распределения случайной величины

Рассмотрим следующие понятия: «эмпирическое распределение СВ», «теоретическое распределение СВ», «закон распределения СВ».

Распределение относительных частот (частостей) называют эмпирическим, а распределение вероятностей - теоретическим.

Законом распределения случайной величины будем называть правило, согласно которому можно определить вероятность попадания случайной величины в любой промежуток.

Ранее мы отмечали, что дискретная случайная величина может быть задана перечислением всех имеющихся значений. Из определения непрерывной случайной величины ясно, что для нее подобная операция неосуществима. Если рассмотреть непрерывную случайную величину Х, возможные значения которой сплошь заполняют интервал [а,в] (покажем на рисунке), то возникает вопрос: можно ли перечислить все возможные значения Х? Ответ, безусловно, отрицателен, так как этот перечень составляет несчетное бесконечное множество. Необходимо ввести метод задания случайных величин, пригодный для любых типов таких величин.

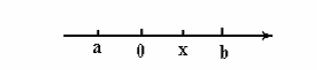
Пусть х - действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, обозначим через Р(Х<х).

Функцией распределения будем называть вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х:

F (x) = P (X < x).

Функция распределения имеет следующие свойства:

1. Значения функции распределения принадлежат отрезку [0,1]

0 £ F(x) £ 1. (1)

2. Функция F(х) - неубывающая функция, т.е. F(x₂)³F(x₁), если х₂³х₁.

Функция распределения удовлетворяет условиям

lim F(x) = 0, lim F(x) = 1. ^x^®^-^¥ ^x^®^+^¥

(2)

Вероятность обнаружения случайной величины Х в интервале x₁<X£x₂ равна

Р (x1 < X £ x2) = F(x2)-F(x1).

(3)

Рассмотрим построение функции распределения на примере с игральной костью. Число очков Х, выпавшее на верхней грани игральной кости, является дискретной случайной величиной. Ее величины можно перечислить: 1, 2, 3, 4, 5 и 6.

Значения функции распределения F(x)=Р(Х<х) приведем в таблице. Например, вероятность того, что выпавшее число очков будет меньше единицы Р(Х<1), равна нулю (невозможное событие), меньше двух Р(Х<2) равна 1/6, а меньшее семи Р(Х<7) - единице (достоверное событие) и т.д.

Значения функции распределения F(x)

Р(Х<1)	Р(Х<2)	Р(Х<3)	Р(Х<4)	Р(Х<5)	Р(Х<6)¦	Р(Х<7)
0/6=0	1/6	2/6=1/3	3/6=1/2	4/6=2/3	5/6	6/6=1

По данным таблицы построим график в координатах F(x) – х (см. рисунок).

Для непрерывной случайной величины график функции распределения будем иметь следующий вид:

Видно, что он удовлетворяет рассмотренным ранее свойствам функции распределения (см. выражения (1)-(3)).

Для непрерывных случайных величин функция распределения имеет производную. Поэтому в статистике широко используют понятие «плотность распределения вероятностей».

Первую производную функции распределения F(x) называют плотностью распределения вероятностей непрерывной случайной величины

.

(4)

Плотность распределения вероятностей удовлетворяет условию f(x)³0.

Покажем график в координатах f(x) – x.

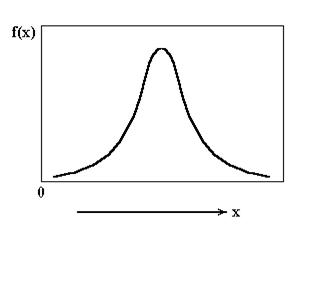
Вероятность попадания случайной величины в интервал х₁<Х£х₂ можно найти через значения плотности распределения вероятностей

.

(5)

Функция распределения F(x) данной случайной величины связана с ее плотностью распределения f(x) соотношением

.

(6)

На основании рассмотренных условий имеем

,

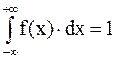т.е. площадь фигуры, заключенной между графиком f(x) и осью 0х, равна единице.

Дата добавления: 2014-01-11