Описание ФАЛ в виде алгебраического выражения

Возможен и аналитический способ записи логической функции. В обычной математике аналитический способ представления функции предполагает запись функции в виде математического выражения, в котором аргументы функции связываются определенными математическими операциями. Подобно этому аналитический способ задания логической функции предусматривает запись функции в форме логического выражения, показывающего, какие и в какой последовательности должны выполняться логические операции над аргументами функции.

Функции одного аргумента (табл. 1.5) представляются следующими выражениями:

f₀ (х) = 0 (константа 0), f ₁ (х) = х,

f₂ (х) = х, f₃ (х) = 1 (константа 1).

Устройства, реализующие функции f₀ (х), f₁ (х) и f₃ (х), оказываются тривиальными. Как видно из рис. 1.1, формирование функции f₀ (х) требует разрыва между входом и выходом с подключением выхода к общей точке схемы, формирование функции f₁ (х) — соединения входа с выходом, формирование функции f₃ (х) — подключения выхода к источнику напряжения, соответствующего лог.1. Таким образом, из всех функций одного аргумента практический интерес может представлять лишь функция f₂ (х) = х (логическое НЕ).

Из сравнения таблиц истинности функций f₀ (х),... f₁₅ (х) (табл. 1.6) с таблицами истинности логических операций (табл. 1.7) следует:

x f₀ (x) x f₁ (x) f₃ (x)

+

-

Рис. 1.1

При описании ФАЛ алгебраическим выражением используются две стандартные формы ее представления.

Дизъюнктивной нормальной формой (ДНФ) называется логическая сумма элементарных логических произведений, в каждое из которых аргумент или его инверсия входит один раз.

Получена ДНФ может быть из таблицы истинности с использованием следующего алгоритма:

а) для каждого набора переменных, на котором ФАЛ равна единице, записывают элементарные логические произведения входных переменных, причем переменные, равные нулю, записывают с инверсией. Полученные произведения называют конституентами единицы;

б) логически суммируют все конституенты единицы.

Пример 1.7. Запись ДНФ для ФАЛ, заданной в примере 1.6.

Р е ш е н и е. Согласно приведенному алгоритму из табл. 1.4 получим:

y (x₂, x₁, x₀) = x₂ x₁ x₀ + x₂ x₁ x_{0 +} x₂ x₁ x_{0 +} x₂ x₁ x₀

Дизъюнктивную нормальную форму, полученную суммированием конституент единицы, называют совершенной (СДНФ).

Конъюнктивной нормальной формой (КНФ) называется логическое произведение элементарных логических сумм, в каждую из которых аргумент или его инверсия входят один раз.

Получена КНФ может быть из таблицы истинности с использованием следующего алгоритма:

а) для каждого набора переменных, на котором ФАЛ равна нулю, записывают элементарные логические суммы входных переменных, причем переменные, значения которых равны единице, записывают с инверсией. Полученные суммы называют конституентами нуля;

б) логически перемножают все полученные конституенты нуля.

Пример 1.8. Запись КНФ для ФАЛ, заданной в примере 1.6.

Р е ш е н и е. Применяя вышеприведенный алгоритм к табл. 1.4, получаем.

y (x₂, x₁, x₀) = (x_{2 +} x_{1 +} x₀)(x_{2 +} x_{1 +} x₀ )(x_{2 +} x_{1 +} x₀)(x_{2 +} x_{1 +} x₀)

Конъюнктивную нормальную форму, полученную суммированием конституент нуля, также называют совершенной (СКНФ).

Рассмотренные методики позволяют получить математическую форму записи для самой функции. Иногда удобнее применять не саму ФАЛ, а ее инверсию. В этом случае при использовании вышеописанных методик для записи СДНФ необходимо выбирать нулевые, а для записи СКНФ — единичные значения функции.

Пример 1.9. Для ФАЛ из примера 1.6 записать СДНФ и СКНФ инверсной функции.

Р е ш е н и е. Воспользовавшись табл. 1.4, запишем:

СДНФ: y (x₂, x₁, x₀) = x₂ x₁ x₀ + x₂ x₁ x_{0 +} x₂ x₁ x_{0 +} x₂ x₁ x₀

СКНФ: y (x₂, x₁, x₀) = (x_{2 +} x_{1 +} x₀)(x_{2 +} x_{1 +} x₀ )(x_{2 +} x_{1 +} x₀)(x_{2 +} x_{1 +} x₀)

Описание ФАЛ в виде последовательности десятичных чисел

Иногда для сокращения записи ФАЛ представляют в виде последовательности десятичных чисел. При этом последовательно записывают десятичные эквиваленты двоичных кодов соответствующих конституент единицы или нуля.

Пример 1.10. Записать в виде последовательности чисел ФАЛ из примеров 1.7 и 1.8.

Р е ш е н и е. В СДНФ из примера 14.7 первая конституента «единица» (х₂ х₁ х_о) соответствует двоичному коду 011 (табл. 1.4). Десятичный эквивалент этого кода равен 3. Аналогично записываются все остальные конституенты:

y (x₂, x₁, x₀) = Σ (3, 5, 6, 7) = V (3, 5, 6, 7)

y (x₂, x₁, x₀) = Π (0, 1, 2, 4) = Λ (0, 1, 2, 4)

Кубические комплексы*

В последнее время широкое распространение получило так называемое кубическое представление ФАЛ. Такое представление использует ограниченное число символов и поэтому применяется при автоматизации процессов логического проектирования цифровых интегральных схем (ИС).

Основой кубической формы является представление каждого набора входных переменных в качестве n-мерного вектора. Вершины этих векторов геометрически могут быть представлены как вершины n -мерного куба. Отмечая точками вершины векторов, для которых ФАЛ равна единице, получаем геометрическое представление функции в виде куба.

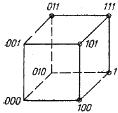
Рис. 14.2. Геометрическое представление ФАЛ

Рис. 14.3. Единичный кубический комплекс ФАЛ (см. пример 1.12)

Рис. 14.4. Двоичный клуб для ФАЛ (см.пример 1.12)

Пример 1.11. Задана ФАЛ z(х_2, х₁, х₀) = Σ (3, 4, 5, б, 7). Дать геометрическое представление в виде куба.

Решение. Графическое решение задачи иллюстрируется рис. 1.2.

Очевидно, что наборы переменных, расположенные на концах ребер куба, отличаются только одной переменной. Такие наборы (коды) принято называть соседними.

Каждую вершину куба, в которой функция принимает единичное значение, называют нулевым кубом (0-кубом). Записывается 0-куб последовательностью образовавших его входных переменных, т. е. кодом, соответствующим констутиенте единицы. Множество нулевых кубов образуют нулевой кубический комплекс К о ФАЛ.

Если два нулевых куба комплекса Ко отличаются только по одной координате (переменной), т. е. два набора переменных, для которых ФАЛ равна единице, являются соседними, то они образуют единичный куб (1-куб). Геометрически это соответствует ребру исходного n -мерного куба (рис. 1.3), 1-куб записывается последовательностью общих элементов образовавших его 0-кубов с прочерком несовпадающих элементов. Множество единичных кубов образует единичный кубический комплекс К₁.

Аналогично,. если два единичных куба комплекса К1 отличаются только по одной координате (переменной), то эти единичные кубы образуют двоичный куб (2-куб). Геометрически это соответствует грани исходного n -мерного куба (рис. 14.4). 2-куб также записывается последовательностью общих элементов, образовавших его 1-кубов с прочерком несовпадающих элементов, а множество двоичных кубов образуют двоичный кубический комплекс К₂. И так далее.

^{*) раздел справочный}

Дата добавления: 2014-01-14