Метод итераций

Рассмотрим уравнение

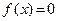(3.1)

Приведем это уравнение каким-либо способом к виду

(3.2)

Выберем начальное приближение x₀ и построим последовательность 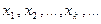по правилу

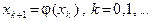(3.3)

Если функция непрерывна и построенная последовательность сходится к x ^* то x * -- решение уравнения. Чтобы убедиться в этом, достаточно перейти к пределу слева и справа.

Геометрический смысл метода: на каждом итерационном шаге через точку

[ x _k, j(x _k ) ] проводим прямую, параллельную оси x, и находим точку ее пересечения с прямой y=x. Абсцисса полученной точки и есть x _k+1. Поясним это на чертеже:

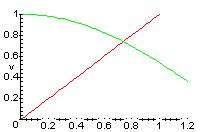
Рассмотрим вопрос о сходимости метода итераций.

Замечание: будем рассматривать только вещественный случай.

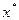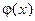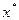Проведем сначала нестрогое исследование сходимости. Пусть — корень уравнения (3.2) и пусть найдено некоторое начальное приближение x ₀, достаточно близкое к корню.Пусть функция имеет непрерывную производную в окрестности , в которой также лежит х₀ . Построим последовательность (3.3). Предположим, что х_k имеет погрешность 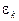, т.е. , а х_k+1 имеет погрешность 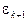, т.е. 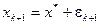. Тогда 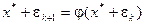. Разложим 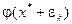в ряд Тейлора в окрестности 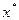. Тогда 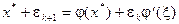, где точка x лежит в окрестности 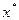. В силу того, что 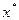— корень уравнения (3.2), получаем 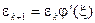, следовательно 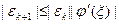. Значит, погрешность будет убывать на каждом шаге метода итераций, если производная от функции j будет по абсолютной величине меньше 1 в нужной окрестности 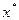.Т.е. достаточным условием сходимости будет условие

(3.4)

При этом, если эта производная положительна, то погрешность сохраняет знак, и сходимость будет с одной стороны. Если же производная отрицательна, то погрешность на каждом шаге будет менять знак, следовательно приближение к корню будет происходить с разных сторон.

Рассмотрим примеры на преобразование уравнений и применение метода итераций.

1) . Это уравнение можно преобразовать к виду . Мы уже видели ранее, что это уравнение имеет единственный корень на промежутке [0,p/2]. Внутри этого промежутка функция 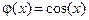удовлетворяет условию (3.4). Поэтому будет сходиться последовательность 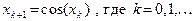. За х ₀ можно взять, например, 1.

2) 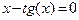. Нельзя положить 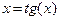, так как для функции 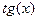никогда не выполнено условие (3.4). Затем встает вопрос, какой корень мы будем искать? Разберемся сначала с этим вопросом. Очевидно, уравнение имеет тривиальный корень х = 0. Затем корень лежит на промежутке [p,3p/2] и дальше еще много корней. Это хорошо видно, если нарисовать графики функций . Предположим, что мы хотим найти наименьший положительный корень. Значит, мы должны искать его в промежутке [p,3p/2]. Теперь займемся преобразованием уравнения. Его можно записать в виде 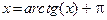. Теперь уже функция 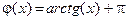всюду на промежутке [p,3p/2] удовлетворяет условию (3.4). За начальное приближение можно взять 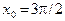и далее построить последовательность 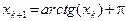, где k= 0, 1, 2,....

О порядке метода итераций.

Определение. Будем говорить, что метод итераций имеет порядок m, если в уравнении (3.2) функция j(х) удовлетворяет условиям: 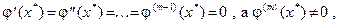где x ^*—корень уравнения (3.2). Порядок метода итераций позволяет определить погрешность вычислений на каждом шаге. Разложим j (х) в ряд Тейлора в окрестности точки x ^*: ,

где x — некоторая точка, лежащая между х и х ^*. Если метод итераций имеет порядок m, то получается 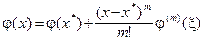. Подставим в это выражение x=x_k: Получим . Но . Значит, . Обозначим через e _k погрешность, допущенную на k -м итерационном шаге. Тогда получим 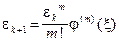, т.е. ошибка, допущенная на предыдущем шаге, возводится в степень m. Поэтому очень важно построить функцию j так, чтобы порядок метода был как можно выше.

В рассмотренных примерах мы выбирали функцию j, исходя из конкретного вида уравнения. Сейчас мы рассмотрим один общий способ построения функции j. Пусть дано уравнение 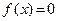. Перепишем его в виде 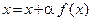, где a — некоторое число, отличное от 0. Положим . Пусть найдено начальное приближение х ₀. Найдем a из условия, что 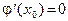. Т.е. . Если функция j непрерывна (а это выполняется, если f (x) непрерывна), и х ₀ выбрано достаточно хорошо, то можно предположить, что в окрестности х _0, где лежит корень, будет выполнено условие 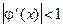. Таким образом, можно взять 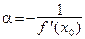. В этом случае метод итераций будет иметь первый порядок. 

Пример. . Найдем начальное приближение. Легко проверить, что наименьший положительный корень этого уравнения лежит внутри промежутка [0,p/2]. Возьмем х₀ = 0.

В этом уравнениии нет наглядного способа построения функции 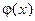, удовлетворяющей условию (3.4). Mожно применить стандартный алгоритм. Перепишем наше уравнение в виде 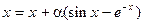. Это уравнение эквивалентно исходному уравнению при любом числовом множителе 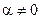. Обозначим 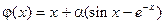. Подберем a из условия 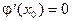. . 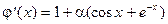У нас х₀ = 0. Значит 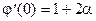= 0. Отсюда 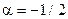. Таким образом, получаем .

Дата добавления: 2014-01-14