Метод итераций для систем уравнений

Рассмотрим задачу о решении системы нелинейных уравнений:

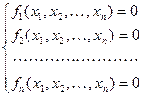(4.1)

Перепишем эту систему в векторной форме:

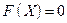, (4.2)

где X= (x₁ ,x₂ ,x₃,...,x_n), F = (f₁ , f₂,..., f_n).

Векторное уравнение (4.2) будем решать методом итераций. Преобразуем это уравнение каким - либо способом к виду

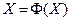(4.3)

Предположим, что мы нашли начальное приближение к решению X₀. Построим последовательность X₁, X₂,...,X_k,... по следующему правилу:

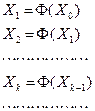(4.4)

Изучим вопрос о сходимости этой последовательности.

Уравнение (4.3) означает, что элемент Х из некоторого метрического пространства R преобразуется в другой элемент того же метрического пространства. F — отображение некоторого элемента пространства R в другой элемент этого же пространства. Обозначим расстояние между двумя элементами X и Y пространства R через . Пусть 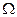— некоторое множество из пространства R: .

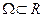Определение: Отображение 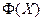называется сжимающим на множестве 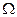, если существует постоянная q: , такая, что для любых двух элементов 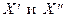из множества 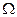имеет место неравенство:

(4.5)

Теорема. Пусть 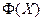— сжимающее отображение на некотором множестве 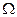. Тогда уравнение (4.3) имеет единственное решение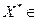 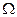, к которому сходится последовательность (3.5.4), при этом для любого n имеет место неравенство

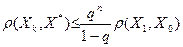(4.6)

где X_n — элемент последовательности (4.4), q — постоянная из неравенства (4.5)

Доказательство. Для любого k = 0, 1,... имеет место неравенство

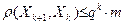, (4.7)

где 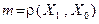. Действительно, используя определение сжимающего отображения, получим: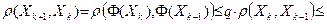

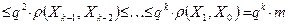. Из неравенства (4.7) получим при любом p= 1,2,...

Сумма в последней скобке есть конечная часть бесконечно убывающей геометрической прогрессии с положительным знаменателем q < 1. Поэтому

(4.8)

Величина, стоящая справа в этом неравенстве, стремится к 0 при любом p. Значит, последовательность, стоящая слева, будет фундаментальной, и значит, она будет иметь предел (критерий Коши). Обозначим его X ^*. Теперь в (4.8) перейдем к пределу при 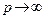. Получим неравенство (4.6). Покажем, что X ^* — корень уравнения (4.3). Справедлива цепочка неравенств:

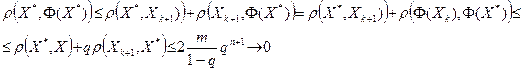
Значит, 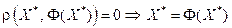, т.е. X ^* — решение уравнения (4.3).

Теперь докажем единственность полученного решения. Пусть Х ^**— еще одно решение уравнения (4.3). Тогда 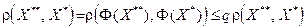. Но q < 1. Следовательно, это неравенство может быть выполнено только при .

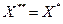Замечание. Эта теорема легко переносится на случай одного уравнения.

Дата добавления: 2014-01-14