Метод Ньютона. Пусть требуется найти корень уравнения

Пусть требуется найти корень уравнения

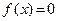(5.1)

Пусть х₀ — начальное приближение. Разложим функцию 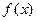в ряд тейлора в окрестности точки х₀ :

где — некоторая точка из окрестности 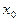. Возьмем в этом разложении линейную часть и запишем уравнение:

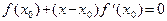(5.2)

Это уравнение линейно. Обозначим его решение через 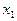. Тогда

Теперь точку 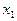считаем приближением к решению уравнения (5.1) и проделываем с ней то же, что и с 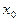. Получаем :

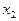Продолжая этот процесс, построим последовательность по правилу:

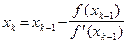, k = 1, 2,... (5.3)

Очевидно, чтобы последовательность (5.3) можно было построить, функция 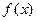не должна обращаться в 0 ни в одной из точек .

Геометрический смысл этого построения.

Уравнение 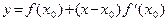является уравнением касательной к кривой 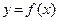в точке 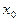. А решение уравнения (5.2) — точка пересечения этой касательной с осью х.

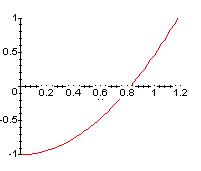
Чтобы изучить вопрос о сходимости последовательности (5.3), перепишем уравнение (5.1) в виде:

(5.4)

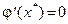Для этого уравнения можно построить последовательные приближения по методу итераций при . Легко показать, что . Действительно, 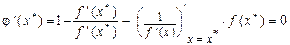, т.к. х ^* — корень уравнения (5.1). В то же время , следовательно, мы получили метод итераций 2-го порядка. Значит, 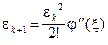, где 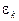— ошибка, полученная на к -м шаге, а — некоторая точка в окрестности корня. Таким

образом, ошибка на каждом следующем шаге возводится в квадрат и если, например, , то сходимость к решению будет очень быстрая. Иногда такую сходимость называют квадратичной

Теперь рассмотрим метод Ньютона для систем уравнений. Пусть дана система нелинейных уравнений:

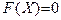(5.5)

где .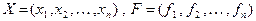

Пусть — начальное приближение к решению системы (5.5).

Замечание. Для систем вопрос о нахождении начального приближения очень сложный, и в общем виде не решается. Его удается решить только в некоторых простых частных случаях. Поэтому чаще всего начальное приближение дается вместе с задачей.

Разложим 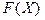в ряд Тейлора, как вектор - функцию от нескольких переменных в окрестности точки :

(5.6)

где 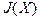— матрица Якоби. Она имеет вид:

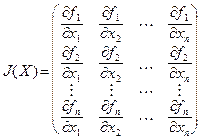(5.7)

Запишем линейную систему:

(5.8)

Эту систему можно считать приближенной к системе (5.5), поэтому ее решение можно считать приближением к решению системы (5.5). Поскольку система (5.8) линейная, мы можем найти ее решение:

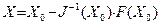
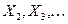Обозначим этот вектор через . Аналогично найдем . Таким образом, мы построим последовательность 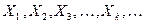по правилу:

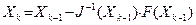(5.9)

Если эта последовательность сходится к пределу и все ограничены, то будет решением системы (5.5). (без доказательства)

Если эта последовательность сходится к пределу и все ограничены, то будет решением системы (5.5). (без доказательства)

Рассмотрим систему 2-х уравнений:

Здесь 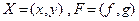. Тогда . Получим линейную систему

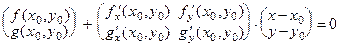. Решая эту систему, получаем приближения по формулам:

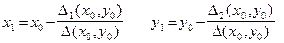
где

Продолжая этот процесс, получаем общие формулы для построения приближенного решения:

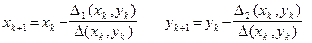, k = 0, 1, 2,... (5.10)

где

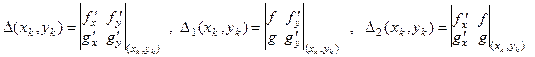
Дата добавления: 2014-01-14