Лекція 4

Питання для роздуму, самоперевірки, повторення

1. Які головні припущення покладено в основу концепції моделі ВСG?

2. Що таке матриця ВСG і як характеризуються її квадранти?

3. Які стратегії пропонуються в моделі ВСG для різних секторів бізнесу?

4. Які інвестиційні пріоритети рекомендуються для „зірок”, „важких дітей”, „дійних корів” та „собак” в моделі ВСG?

5. Які недоліки і обмеження моделі ВСG ви можете назвати?

6. Що являє собою модель GE/McKinsey? Яка її головна мета?

7. За якими правилами будується матриця GE/McKinsey і як хара-ктеризуються позиції різних видів бізнесу в її стратегічному просторі?

8. Які фактори аналізуються для визначення загальної оцінки сильних сторін бізнесу та його ринкової привабливості у моделі GE/McKinsey?

9. Які стратегії рекомендуються Нейлором і Деєм для різних позицій бізнесу?

10. Які недоліки мас модель GE/McKinsey? Чші вона відрізняється від моделі ВСG (назвіть як позитивні, так і негативні відмінності)?

11. Охарактеризуйте зміст моделі Shell/DPM і рекомендовані нею стратегії.

12. Які напрями розвитку підприємства вважаються оптимальними з погляду моделі Shell/DPM?

13. Які позитивні і негативні сторони моделі Shell/DPM ви можете назвати? У чому її відмінність від моделей ВСG і GE/McKinsey?

Диференціальні рівняння вищих порядків. Задача Коші. Теорема існування та єдиності розв’язку задачі Коші. Загальний та частинний розв’язки. Диференціальні рівняння вищих порядків, що допускають пониження порядку.

Рівняння

, (4.1)

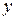де – незалежна змінна, – шукана функція, а 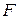визначена й неперервна в деякій області та залежна від , називається звичайним диференціальним рівнянням n-го порядку.

Диференціальне рівняння n -го порядку, розв’язане відносно старшої похідної, має вигляд:

, (4.2)

де функція неперервна в деякій області 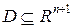зміни своїх аргументів.

Розв’язком рівняння (4.2) на інтервалі називається функція , яка задовольняє умови:

1) неперервно диференційована 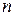разів на ;

2) ;

3) перетворює рівняння (4.2) в тотожність, тобто

.

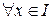Аналогічно означається розв’язок рівняння (4.1).

Задачею Коші або початковою задачею для рівняння (4.2) називається задача знаходження такого розв’язку рівняння (4.2), який задовольняє початкові умови:

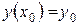, , (4.3)

де 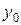,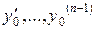– задані числа.

Теорема Пеано. Якщо функція неперервна в області 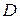, то для будь-якої точки 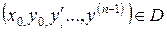існує розв’язок рівняння (4.2), визначений в деякому околі точки 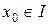, який задовольняє початкові умови (4.3).

Існування та єдинність розв’язку задачі Коші гарантує наступна теорема.

Теорема Коші-Пікара. Якщо функція неперервна в області 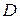і задовольняє умову Ліпшіца по змінних , то для будь-якої точки 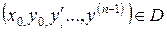існує розв’язок рівняння (4.2), визначений в деякому околі точки 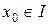, який задовольняє початкові умови (4.3).

Умови теореми Коші-Пікара виконуються, зокрема, якщо функція неперервна на 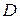і має в околі точки обмежені частинні похідні по , .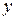

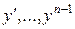Нехай 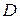– область, в кожній точці якої задача Коші для рівняння (4.2) має єдиний розв’язок. Функція

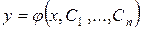, (4.4)

де довільні сталі, називається загальним розв’язком рівняння (4.2) в області 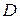, якщо:

1) функція 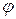має неперервні частинні похідні по до 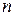-го порядку включно;

2) для будь-якої точки система

……………………

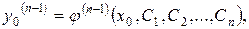
має єдиний розв’язок відносно :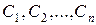

,

,

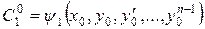………………………. (4.5)

;

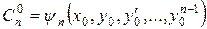3) функція є розв’язком рівняння (4.2) при будь-яких допустимих значеннях 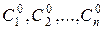, які визначаються рівностями (4.5), при умові, що точка 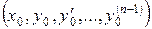належить області .

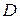Якщо загальний розв’язок (4.4) в області 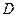заданий неявно співвідношенням

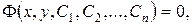(4.6)

то (4.6) називають загальним інтегралом рівняння (4.2) в області .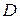

Розв’язок, який можна знайти з (4.4) при конкретних числових значеннях називають частинним розв’язком рівняння (4.2). Якщо відомий загальний розв’язок (4.4), то розв’язати задачу Коші можна так. Із співвідношень (4.4) або (4.6) і тих, які дістають за допомогою 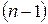-кратного диференціювання по з використанням початкових умов (4.3), складають систему рівнянь для визначення 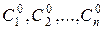, підставивши їх в (4.4) або (4,6), дістанемо розв’язок задачі Коші

(4.7)

або частинний інтеграл , яким неявно задається розв’язок задачі Коші.

Для рівняння (4.1), не розв’язаного відносно похідної , задача Коші ставиться аналогічно задачі Коші для рівняння (4.2). При цьому, якщо заданим числам і кожному із значень , які визначаються з рівняння

,

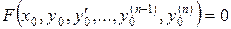відповідає лише один розв’язок, то кажуть, що задача Коші має єдиний розв’язок.

Теорема (існування і єдиності розв’язку задачі Коші для рівняння (4.1)). Нехай функція 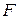неперервна в області 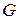і має неперервні частинні похідні по 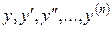. Тоді для будь-якої точки 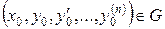такої, що

, ,

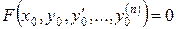Існує єдиний розв’язок рівняння (4.1), визначений в деякому околі точки , який задовольняє початкові умови (4.3).

Якщо – розв’язок рівняння (4.1), то множина точок 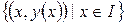, тобто графік розв’язку , називається інтегральною кривою рівняння (4.1). З геометричної точки зору розв’язок (загальний інтеграл) є сім’єю інтегральних кривих на площині, яка залежить від 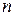параметрів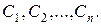

Співвідношення виду

(4.8)

де 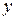- розв’язок рівняння (4.1), здобуте внаслідок інтегрування рівняння (4.1), називається проміжним інтегралом 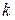-го порядку рівняння (4.1).

Якщо відомий проміжний інтеграл 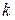-го порядку (4.8), то задача інтегрування рівняння 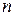-го порядку (4.1) зводиться до простішої задачі інтегрування рівняння -го порядку (4.8). Проміжний інтеграл

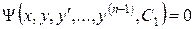, (4.9)

називається першим інтегралом.

Якщо відомо 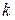різних перших інтегралів, то порядок рівняння можна знизити на 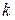одиниць. Якщо відомо 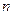різних перших інтегралів, то, виключивши з них всі похідні 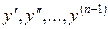, дістанемо загальний інтеграл рівняння.

Функція називається особливим розв’язком диференціального рівняння (4.1), якщо:

1)перетворює диференціальне рівняння в тотожність;

2) для будь-якої точки задача Коші з початковими умовами

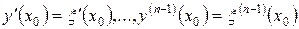(4.10)

має більш як один розв’язок.

Приклад 1. Показати, що функція , неявно задана рівнянням

є розв’язком рівняння

Розв’язання. Знаходимо

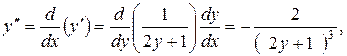
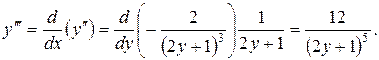
Підставимо останні три рівності у рівняння умови:

Отже, функція є розв’язком даного рівняння.

Розглянемо окремі види рівнянь вищих порядків, інтегровані в квадратурах.

а) рівняння, які містять лише похідну 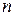-го порядку шуканої функції і незалежну змінну.

Розглянемо рівняння

(4.11)

У багатьох випадках рівняння (4.11) можна параметризувати: 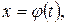де – диференційована функція. У цьому випадку можна знайти загальний інтеграл в параметричній формі. Маємо , , 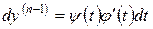звідки

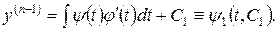
Аналогічно знаходимо тощо. Для 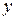дістаємо вираз виду Тому система 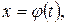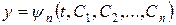є загальним інтегралом рівняння (4.11) у параметричній формі. Окремим випадком (4.11) є рівняння

(4.12)

де - неперервна функція на .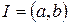

Якщо вважати параметром, то загальний розв’язок рівняння (4.12) дістанемо у вигляді

.

Загальний розв’язок рівняння (4.12) у формі Коші має вигляд

де 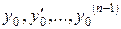– будь-які числа.

Приклад 3. Побудувати загальний розв’язок рівняння

у формі Коші і знайти частинний розв’язок цього рівняння, який задовольняє початкові умови

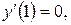
Розв’язання. Рівняння такого виду розглянуто в п. а). За допомогою послідовного інтегрування знаходимо

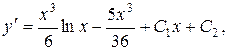
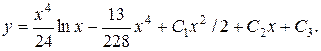
Сталі знайдемо із системи

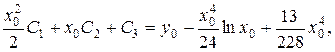
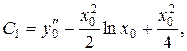
Маємо:

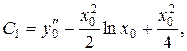
Звідси дістанемо загальний розв’язок рівняння у формі Коші:

Поклавши 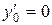, , дістанемо шуканий частинний розв’язок

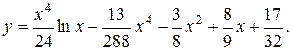
б) Рівняння виду

(4.13)

Якщо рівняння (4.13) можна розв’язати відносно , тобто

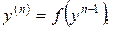(4.14)

то, ввівши нову невідому функцію , рівняння (4.14) зведемо до виду

. (4.15)

Загальним інтегралом рівняння (4.15) є

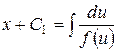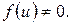, (4.16)

Припустимо, що (4.16) можна розв’язати відносно :

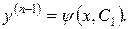(4.17)

Оскільки (4.17) є рівняння типу (4.12), то загальний розв’язок рівняння (4.13) дістанемо у вигляді

Якщо рівняння (4.13) задано в параметричній формі 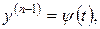де – диференційована функція. то його інтегрують так.

Із співвідношення дістають

звідки

(4.18)

Далі

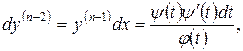
(4.19)

.

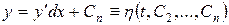сукупність (4.18), (4.19) є загальним інтегралом рівняння (4.13) у параметричній формі.

Приклад 4. Знайти загальний розв’язок рівняння

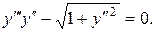
Розв’язання. Задане рівняння не розв’язане відносно Ліва частина рівняння – функція 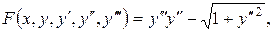вона неперервна і має неперервні частинні похідні:

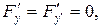
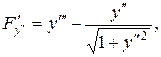
Тому, внаслідок теореми існування і єдиності, задача Коші для такого рівняння з будь-якими початковими умовами виду має єдиний розв’язок. Функція 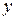така, що 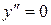не є розв’язком даного рівняння. Рівняння належить до типу, який було розглянуто в п. б). поклавши , зведемо рівняння до вигляду

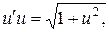
звідки

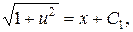
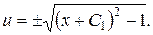
В результаті послідовного інтегрування знаходимо:

де – довільні сталі. Знак “плюс” відповідає загальному розв’язку для області знак “мінус” – для області визначення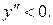

в) Рівняння виду

(4.20)

за допомогою заміни

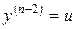(4.21)

рівняння (4.20) зводиться до рівняння другого порядку

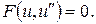(4.22)

Припустимо, що рівняння (12) можна розв’язати відносно :

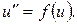(4.23)

помноживши (4.23) на інтегрувальний множникдістанемо

(4.24)

З (4.24) маємо перший інтеграл рівняння (4.23):

. (4.25)

Звідси знаходимо

Тоді загальний інтеграл рівняння (4.23) має вигляд

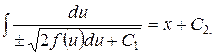. (4.26)

Врахувавши заміну (4.21), з (4.26) дістанемо проміжний інтеграл рівняння (4.20) виду

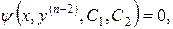
тобто диференціальне рівняння 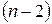-го порядку типу (4.11), яке інтегрується в квадратурах.

Якщо рівняння (4.20) задано в параметричному вигляді 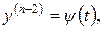то його інтегрують так.

Із співвідношень 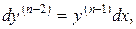дістаємо рівняння відносно виду

звідки

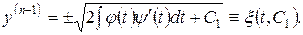
Отже, для маємо параметричне зображення яке вже зустрічалося при інтегруванні рівняння (4.13).

Приклад 5. Знайти розв’язок задачі Коші

,

Розв’язання. Рівняння такого типу розглянуто в п. в). Враховуючи, що , дістанемо

Помножимо на інтегрувальний множник 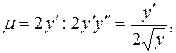звідки

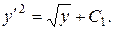
Сталу 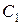знайдемо з початкових умов. Підставивши у , , 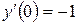дістанемо, що . Оскільки 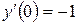, то 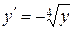. Тоді

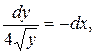
Враховуючи початкові умови, дістаємо Тому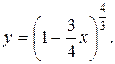

г) Рівняння, які не містять шуканої функції і кількох послідовних похідних.

Розглянемо рівняння виду

. (4.27)

За допомогою заміни , де – нова невідома функція, рівняння (4.27) можна звести до рівняння 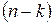– го порядку:

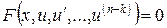. (4.28)

Якщо рівняння (4.28) інтегрується в квадратурах, то, повертаючись до змінної 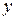, отримаємо проміжний інтеграл рівняння (4.27):

, або (4.29)

Рівняння (4.29) є рівняннями виду (4.11).

Приклад 6. Проінтегрувати рівняння

.

Розв’язання. Рівняння не містить шуканої функції та її похідної. Поклавши 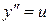, де – нова шукана функція, отримаємо

.

Відокремлюємо змінні при , 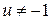. Маємо

, , ,

,

, , .

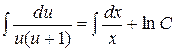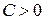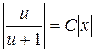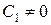Звідси . За допомогою послідовного інтегрування знаходимо:

,

.

де 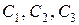– довільні сталі, .

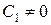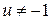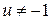Розглянемо випадки , . Якщо , то ; якщо , то

,

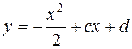де – довільні сталі. За допомогою підстановки впевнюємося в тому, що ці функції також є розв’язками даного рівняння.

д) Рівняння, які явно не містять незалежної змінної.

Розглянемо рівняння виду

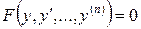(4.30)

За допомогою заміни

, (4.31)

де – нова шукана функція, 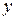– нова незалежна змінна, порядок рівняння (4.30) можна знизити на одиницю, оскільки

,

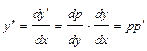(4.32)

………………………………

,

, і=1,2,…,n-1.

Підставивши (4.30), (4.31) в (4.32), отримаємо рівняння -го порядку відносно нової шуканої функції :

. (4.33)

Якщо відомий загальний інтеграл рівняння (4.33):

,

то співвідношення

(4.34)

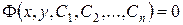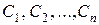є проміжним інтегралом -го порядку рівняння (4.30) – диференціальним рівняння першого порядку інтегровного типу. Загальний інтеграл рівняння (4.34), який має вигляд , де – довільні сталі, є загальним інтегралом рівняння (4.30).

При виконанні заміни (4.31) можлива втрата розв’язків виду . Безпосередньою підстановкою необхідно перевірити, чи справді рівняння (4.30) має такі розв’язки.

е) Рівняння, однорідні відносно .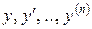

Розглянемо рівняння виду

(4.35)

де функція 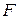є однорідною відносно 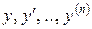із степенем однорідності m, тобто

, l>0.

За допомогою заміни

, (4.36)

де – нова невідома функція, порядок рівняння (4.35) можна знизити на одиницю.

Маємо:

, (4.37)

…………………

.

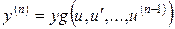Підставивши (4.37) y (4.35), дістанемо

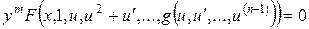. (4.38)

Скоротивши рівняння (4.38) на (розв’язок не втратиться), дістанемо диференціальне рівняння -го порядку відносно функції :

. (4.39)

Якщо відомий загальний розв’язок 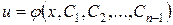рівняння (4.39), то, як випливає з (4.36), загальний розв’язок рівняння (4.35) має вигляд:

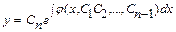, (4.40)

де 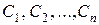– довільні сталі. Розв’язок дістаємо з (4.40) при .

Приклад 7. Проінтегрувати рівняння

.

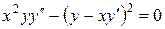Розв’язання. Ліва частина рівняння – однорідна функція відносно змінних зі степенем однорідності 2.

.

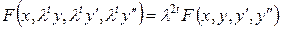Виконаємо заміну ,, де – нова невідома функція. Тоді

,

.

Функція є розв’язком заданого рівняння. При маємо

,

звідки для функції дістаємо лінійне неоднорідне рівняння першого порядку:

.

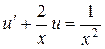Загальний розв’язок цього рівняння:

.

Враховуємо заміну :

,

.

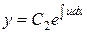Розв’язок маємо при .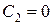

Контрольні запитання

1. Яке рівняння називається звичайним диференціальним рівнянням 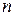-го порядку?

2. Що є його розв’язком?

3. Сформулюйте задачу Коші для звичайного диференціального рівняння 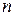-го порядку.

4. Що називається загальним, частковим та особливим розв’язком рівняння 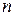-го порядку?

5. Що називається загальним інтегралом рівняння 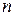-го порядку?

6. Які рівняння вищих порядків інтегровані в квадратурах?

7. Які рівняння вищих порядків допускають пониження порядку на одиницю?

Дата добавления: 2014-01-14