Квадратурные формулы наивысшей алгебраической степени точности

Рассмотрим снова квадратурную формулу в общем виде:

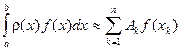(6.1)

(остаточный член пока не будем рассматривать). Было показано, что интерполяционные квадратурные формулы имеют алгебраическую степень точности не меньше n -1. Поставим вопрос: нельзя ли распорядиться выбором узлов квадратурной формулы (6.1), таким образом, чтобы увеличить ее алгебраическую степень точности? Ответ на этот вопрос раньше всех дал Гаусс для случая, когда промежуток конечен, а весовая функция . Затем это утверждение было обобщено на случаи положительной весовой функции и для бесконечных промежутков. Мы сейчас рассмотрим общий случай.

Будем предполагать, что 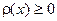, причем существует . Пусть существуют интегралы: 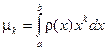, k= 1,2,....

Определение. Будем говорить, что функции 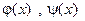ортогональны с весом 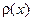на промежутке [a,b], если .

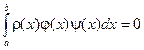В построении квадратурных формул большую роль играют ортогональные многочлены.

Теорема 1. (о корнях ортогональных многочленов).

Пусть — многочлен степени n, ортогональный ко всем многочленам степени меньше n с весом 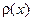на промежутке [a,b]. Тогда все его корни вещественны, различны и лежат на промежутке [a,b].

Доказательство. По условию теоремы многочлен ортогонален 1. Значит,

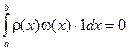. Это значит, что подинтегральная функция имеет на промежутке интегрирования вещественные корни нечетной кратности. Но 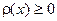, значит, имеет на промежутке [a,b] вещественные корни нечетной кратности. Пусть таких корней будет m. Обозначим их . При этом 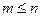. Составим многочлен . Рассмотрим многочлен . У этого многочлена внутри [a,b] все вещественные корни будут только четной кратности, следовательно, он на [a,b] сохраняет знак. Тогда 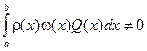. Но по условию теоремы многочлен ортогонален всем многочленам, степень которых меньше n. Значит, многочлен Q (x) имеет степень n. Следовательно, m=n. Таким образом, все корни многочлена имеют первую кратность. Этим и доказывается теорема. g

Теперь обратимся к квадратурной формуле. Имеет место

Теорема 2. Для того, чтобы квадратурная формула (6.1) была точна для любого могочлена степени 2n-1, необходимо и достаточно, чтобы

1) она была интерполяционной,

2) ее узлы 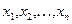— корни многочлена ,

ортогонального с весом 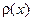на промежутке [a,b] к любому многочлену Q(x) степени < n.

Дата добавления: 2014-01-14