Полиномы Лежандра и квадратурная формула Гаусса

Пусть и промежуток равен [-1,1]. Полиномы, ортогональные с весом 1 на промежутке [-1,1], называются полиномами Лежандра. Рассмотрим многочлен степени n:

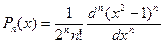(7.1)

Покажем, что этот многочлен ортогонален с весом 1 на промежутке [-1,1] ко всем многочленам степени меньше n. Обозначим

(7.2)

Тогда

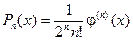(7.3)

Очевидно, при k = 0, 1, 2,..., n -1 .

Пусть Q (x) — любая, n раз непрерывно дифференцируемая на промежутке [-1,1] функция. Рассмотрим интеграл от функции :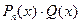

.

Проинтегрируем интеграл справа по частям:

.

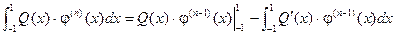Следовательно,

Продолжаем интегрирование по частям, пока не получим справа . Тогда:

(7.4)

Пусть Q (x) — любой многочлен степени < n. Тогда Q⁽ⁿ⁾ (x) = 0. Значит,

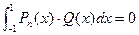(7.5)

А это и означает, что P_n (x) ортогонален с весом 1 на промежутке [-1,1] ко всем многочленам степени меньше n.

Приведем выражение справа в (7.1) к канонической форме:

(7.6)

Это было нужно, чтобы определить старший коэффициент многочлена P_n (x). Чтобы получить многочлен со старшим коэффициентом 1, нужно поделить на этот коэффициент. Таким образом:

(7.7)

Возьмем в формуле (7.4) в качестве Q (x) многочлен P_n (x). Тогда

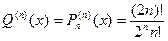
Следовательно,

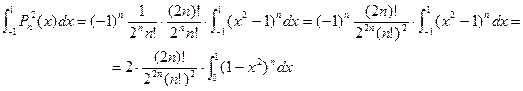(7.8)

Вычислим стоящий справа интеграл, обозначив его I_n.

. Сделаем в этом интеграле замену переменных, положив 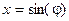. Тогда 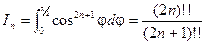. Следовательно,

Подставим полученное выражение в (7.8). Окончательно получаем:

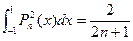(7.9)

Найдем еще значения P_n (x) на концах промежутка [-1,1]. Для этого воспользуемся формулой Лейбница для производной от произведения двух функций:

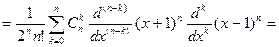
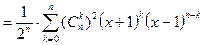
В частности,

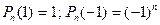(7.10)

Таким образом, мы можем теперь найти все корни многочлена P_n (x), и они будут узлами квадратурной формулы. Обозначим их . Коэффициенты находим по формуле

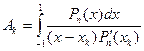(7.11)

Получим для вычисления более удобную формулу. Рассмотрим при фиксированном k некоторое число , вычисляющееся с помощью выражения

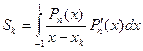(7.12)

Подинтегральная функция справа является многочленом степени 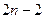, следовательно для нее точна формула Гаусса. Таким образом получаем

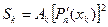(7.13)

Теперь посчитаем по-другому. Проинтегрируем (7.12) по частям:

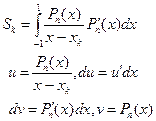
Тогда

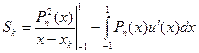(7.14)

u — многочлен степени n- 1, значит, u ¢ — многочлен степени, меньшей чем n- 1, а 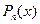по условию ортогонален всем многочленам степени, меньшей чем n- 1, значит, 2-й интеграл в правой части (7.14) равен 0, т.е.

Приравняем это значение и выражение справа в (7.13):

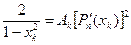
Т.е.

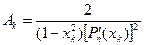(7.15)

Эта формула удобна тем, что не нужно вычислять интегралы.

Формула, у которой узлы — корни многочлена (7.1) ,а коэффициенты вычисляются по формуле (7.15), называется формулой Гаусса.

Коэффициенты формулы Гаусса вычислены при различных n и приводятся в справочной литературе, например, в книге: Крылов В.И. “Приближенное вычисление интегралов”.

Там же приводятся и узлы квадратурной формулы, т.е. корни многочлена P_n (x) при различных n.

Замечание. Если промежуток произвольный, но конечный, т.е. нужно вычислять , то нужно воспользоваться подобными формулами из §2.

Дата добавления: 2014-01-14