Постановка задачи. Численные методы решения систем уравнений

Лекция 9.

Численные методы решения систем уравнений.

«Постановка задачи. Метод Гаусса с выбором главного элемента.»

Так как существует целый класс задач, сводящихся к решению систем линейный алгебраических уравнений, в которых число уравнений совпадает с числом неизвестных, а определитель системы отличен от нуля, то, прежде всего, следует научиться решать такие системы, тем более, что системы нелинейных уравнений часто сводятся к системам линейных уравнений.

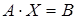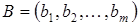Итак, пусть требуется решить систему линейных алгебраических уравнений , где A – матрица коэффициентов системы , – искомый вектор, – заданный вектор правых частей. Предположим, что определитель матрицы A отличен от 0 () и, следовательно, решение X существует и единственно.

Для большинства вычислительных задач характерным является большой порядок матрицы A. Из курса алгебры известно, что систему 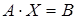можно решить по крайней мере тремя способами: по формулам Крамера, матричным или методом последовательного исключения неизвестных Гаусса. Из них наиболее удобным для реализации на ЭВМ является метод Гаусса.

Методы численного решения систем 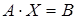делятся на две группы: прямые и итерационные. В прямых (или точных) методах решение X системы 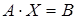находится за конечное число арифметических действий. Примером прямого метода является метод Гаусса. Отметим, что вследствие погрешностей округлений при решении задач на ЭВМ, прямые методы на самом деле не приводят к точному решению системы 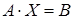, и называть их точными можно только отвлекаясь от погрешностей округления.

Итерационные методы (методы последовательных приближений) состоят в том, что решение x – системы 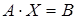находится как предел при 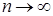последовательности приближений 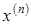, где n – номер итерации. Как правило, за конечное число итераций этот предел не достигается. Обычно задается некоторое малое число , и вычисления проводятся до тех пор, пока не будет выполнено условие , где 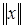– одна из норм в пространстве 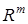, например: 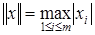или .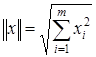

Прямые методы на практике применяются для матриц умеренного порядка (m – порядка 100). Для матриц высокого порядка предпочтительнее итерационные методы.

Дата добавления: 2014-01-14