Предельные теоремы теории вероятностей

Схема Бернулли

Замечание. В научной и практической деятельности постоянно приходится проводить многократно повторяющиеся испытания в сходных условиях (физический и технический эксперимент, метеорология, организация производства и т.д.). Как правило, при этом результаты предшествующих испытаний никак не сказываются на последующих. Очень важен простейший тип таких испытаний, когда в каждом из испытаний некоторое событие А может появиться с одной и той же вероятностью р и эта вероятность остаётся одной и той же, независимо от результатов предшествующих и последующих испытаний. Этот тип событий был исследован Якобом Бернулли и называется схемой Бернулли. Схема Бернулли положила начало многим дальнейшим построениям и обобщениям теории вероятностей.

Пусть проводится серия из n независимых испытаний, в каждом из которых с вероятностью р может наступить некоторое событие А.

В схеме Бернулли под элементарным событием принято понимать последовательность наступлений или ненаступлений события А в данной последовательности испытаний.

Пример. Серия подбрасываний монеты.

В общем случае. 1- А наступило, 0 – не наступило. При n построить множество всех элементарных событий. Подсчитать общее число исходов (размещения с повторениями): .

Введём вероятностную меру на этом множестве элементарных событий. Вероятность наступления события А в испытании с номером k равна р, а его ненаступления – q=1-p. Наступление или ненаступление события А в испытаниях с разными номерами для схемы Бернулли независимы. Значит, в силу теоремы умножения вероятностей, вероятность того, что событие А наступит в m определённых испытаниях (например с номерами s₁, s₂, …, s_m), а в остальных n-m не наступит, равна . Эта вероятность не зависит от того, как расположены номера s₁, s₂, …, s_m.

Простейшая задача, относящаяся к схеме Бернулли, состоит в определении вероятности 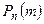того, что в n испытаниях событие А произойдёт m раз ().

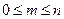Вероятность того, что событие А наступит в m испытаниях с определёнными m номерами, а в остальных не наступит, равна . При реализации серии из n испытаний может реализоваться только одна последовательность m наступлений и n-m ненаступлений события А в n испытаниях. Различные комбинации такого рода несовместны. Тогда по теореме сложения искомая вероятность равна сумме только что вычисленных вероятностей для всех различных последовательностей m появлений события А и n-m непоявлений среди n испытаний.

Вычислим число всех таких последовательностей. Рассматривается совокупность из n элементов (число испытаний). Эта совокупность делится на 2 однородных группы из m и n-m элементов (m появлений и n-m непоявлений события А). Различные последовательности отличаются порядком появлений и непоявлений события А (порядок важен), все появления одинаковы, различимы только номером (повторения есть), все непоявления также одинаковы, различимы только номером (повторения есть). Следовательно, число всех таких последовательностей это перестановки с повторениями из n элементов, делящихся на 2 однородных группы. Их число: .

Тогда искомая вероятность - формула Бернулли. (1)

Легко видеть, что вероятность 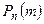равна коэффициенту при в разложении бинома по степеням . В силу этого свойства совокупность вероятностей 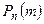называют биномиальным законом распределения вероятностей.

Замечание 1. Аналогично, полученный результат можно обобщить на случай k событий. А именно, если в каждом испытании может произойти одно и только одно из k событий А₁, А₂, …, А_k, испытания независимы, и в каждом из них событие А_i происходит с вероятностью р_i, то вероятность того, что в n независимых испытаниях появятся m₁ событий А₁, m₂ событий А₂, …M_k событий А_k, равна

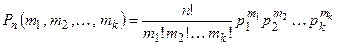. (1’).

Легко убедиться в том, что эта вероятность является коэффициентом при в разложении полинома по степеням х₁, х₂, …, х_k. Вероятности (1’) называют полиномиальным распределением.

Замечание 2. Так как все возможные несовместимые исходы испытаний состоят в появлении события А 0 раз, 1 раз, 2 раза, …, n раз, то ясно, что 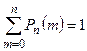. Это соотношение может быть выведено и без учёта теоретико-вероятностных соображений, поскольку по формуле бинома Ньютона .

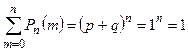Пример 1. Вероятность того, что расход электроэнергии на продолжении одних суток не превысит установленной нормы, равна . Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

Решение. Вероятность нормального расхода электроэнергии на продолжении каждых из 6 суток постоянна и равна . Тогда вероятность того, что расход электроэнергии в течение 4 суток из 6 не превысит нормы, по формуле Бернулли равна: .

Пример 2. Вероятность изделию некоторого производства оказаться бракованным равна 0б005. Чему равна вероятность того, что из 10000 наудачу взятых изделий бракованных изделий окажется а) ровно 40; б) не более 70?

Решение. n=10000, p=0,005. Поэтому по формуле (1) находим

а);

б) вероятность того, что число бракованных изделий окажется не больше 70, равна сумме вероятностей числу бракованных изделий оказаться равным 1, 2, 3, …, 70. Таким образом: .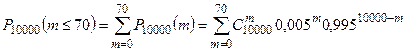

Замечание. Пример 2 показывает, что при решении подобных задач возникают задачи, требующие приближенного вычисления сумм 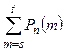для заданных t и достаточно больших n. Точно также необходимы приближённые формулы для вычисления вероятностей 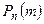при больших значениях m и n или же при малых m, но больших n.

Установим некоторые свойства поведения 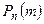как функции от m. Для . Отсюда следует, что

1) если (или ), то ;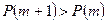

2) если (или ), то ;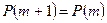

3) если (или ), то .

То есть вероятность 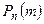с увеличением m сначала возрастает, затем достигает максимума, и при дальнейшем росте m убывает. При этом если является целым числом, то максимальное значение вероятность 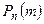принимает для двух значений m, а именно для и 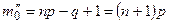. Если не является целым числом, то максимального значения вероятность 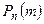достигает при , равном наименьшему целому числу, большему .

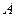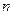Определение. Число называется наивероятнейшим числом наступлений события в испытаниях, если значение 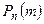при не меньше остальных значений 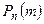, то есть 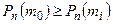при .

Есл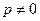и и , то число можно определить из двойного неравенства:

.

Разность граничных значений в этом двойном неравенстве равна 1. Если является целым числом, то имеется 2 наивероятнейших значения и .

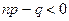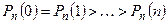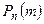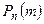Замечание. Если , то , а если , то . В дальнейшем будет доказано, что при больших значениях n вероятности становятся близкими к нулю, но только для m, близких к , вероятности сколько-нибудь заметно отличаются от нуля.

Пример 3. Найти наивероятнейшее значение дней для примера 1.

Пример 4. Для 15 бросаний монеты.

Дата добавления: 2014-01-14