Симплекс-метод с естественным базисом

Симплексный метод решения задачи

Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж. Данцигом около 50 лет назад. Суть этого метода заключается в том, что:

1) вначале исходная ЗЛП записывается в канонической форме;

2) предварительно получают допустимый вариант, удовлетво­ряющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение);

3) полученный вариант проверяется на оптимальность с помощью критерия оптимальности;

4) если решение не оптимальное, переходят к следующему опорному решению (плану) на основе применения метода Жордана-Гаусса для системы линейных уравнений; на­правление перехода от одного опорного решения к другому выбирается на основе критерия оптимальности исходной задачи;

5) полученный опорный план снова проверяется на опти­мальность и т. д. Оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций), причем на последнем шаге либо выявляется нераз­решимость задачи (конечного оптимума нет), либо получа­ются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.

Симплекс-метод осно­ван на следующих свойствах ЗЛП:

1. Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.

2. Множество всех планов задачи линейного программиро­вания выпукло.

3. Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранни­ка решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в од­ной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комби­нацией этих точек.

4. Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.

Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).

Для примене­ния этого метода ЗЛП должна быть сформулирована в кано­нической форме (2.12) - (2.14). Решение ведется в симплекс-таблицах:

Таблица 1

№ симплекс-таблицы

Базис

Сб

План В

с1

с2

…

сm

…

сj

…

сk

…

сn

Q

A1

A2

…

Am

…

Aj

…

Ak

…

An

0

A1

с1

b1

a11

a12

…

a1m

…

a1j

…

a1k

…

a1n

A2

с2

b2

a21

a22

…

a2m

…

a2j

…

a2k

…

a2n

…

…

…

…

…

…

…

…

…

…

…

…

…

Ai

сi

bi

ai1

ai2

…

aim

…

aij

…

aik

…

ain

…

…

…

…

…

…

…

…

…

…

…

…

…

Ar

сr

br

ar1

ar2

…

arm

…

arj

…

ark

…

arn

…

…

…

…

…

…

…

…

…

…

…

…

…

Am

сm

bm

am1

am2

…

amm

…

amj

…

amk

…

amn

L

…

…

Δ j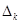

…

…

Матрица системы уравнений должна содержать единичную подматрицу раз­мерностью т х т. В этом случае очевиден начальный опор­ный план (неотрицательное базисное решение).

Для определенности предположим, что первые т век­торов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план:
(b₁, b₂,..., b_m,0,...,0). Т.е. основные переменные являются свободными и равными нулю, а дополнительные переменные являются базисными и равны правым частям СЛУ.

Признак оптимальности заключается в следующих двух теоремах.

Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие

<0, где , j =, (т.е. - скалярное произведение векторов столбцов С_б и A_j),

то можно получить новый опорный план, для которого зна­чение целевой функции будет больше исходного; при этом могут быть два случая:

а) если все координаты вектора, подлежащего вводу в базис, неположительны, то ЗЛП не имеет решения;

б) если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.

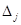мы будем называть оценкой столбца j.

Теорема 2. Если для всех векторов выполняется условие , то полученный план является оптимальным.

На основании признака оптимальности в базис вводится вектор A_k, давший минимальную отрицательную величину симплекс-разности:

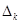= z_k - c_k = min (z_j - c_j), j =, (т.е. имеющий минимальную отрицательную оценку)

Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор А_r, который дает минимальное положительное отношение

Q = , a_ik>0, i= .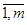

Строка A_r называется направляющей, столбец А_k и эле­мент a_rk — направляющими (последний называют также разрешающим или ведущим элементом).

Элементы вводимой строки, соответствующей направ­ляющей строке, в новой симплекс-таблице вычисляются по формулам (они – есть следствие (формализация) метода Жордана-Гаусса).

, ,

а элементы любой другой i -oй строки пересчитываются по формулам:

, i= ,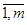

Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:

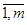для i=r; , i= для .

Число L в симплексной таблице –это текущее значение целевой функции.

, т.е. скалярное произведение векторов столбцов С_б и В.

Если наименьшее значение Q достигается для несколь­ких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить сле­дующий способ.

Вычисляются частные, полученные от деления всех эле­ментов строк, давших одинаковое минимальное значение Q, на свои направляющие элементы. Полученные частные со­поставляются по столбцам слева направо, при этом учиты­ваются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответст­вующий строке, в которой раньше обнаружится меньшее частное.

Для использования приведенной выше процедуры сим­плекс-метода к минимизации линейной формы f( ) следует искать максимум функции f₁( ) = - f( ), затем получен­ный максимум взять с противоположным знаком. Это и бу­дет искомый минимум исходной ЗЛП.

Рассмотрим алгоритмы симплекс-метода на конкретной задаче.

▼

Пример. Для производства продукции типа П₁ и П₂ предприятие использует два вида сырья: С₁ и С₂. Данные об условиях приведены в таблице.

Таблица 2

Сырье	Расход сырья на единицу продукции, кг/ед.	Количество сырья, кг
П1	П2
С1
С2
Прибыль, тыс.руб/ед.прод.

Составить план производства по критерию «максимум прибыли».

Решение. Обозначим объем производства продук­ции П₁ через x₁, продукции П₂ - через x₂. С учетом этих обозначений математическая модель задачи имеет вид:

max f( ) = 2 x₁ +3 x₂

при ограничениях x₁+ 3x₂300,

x₁+ x₂150,

x₁0; x₂ 0.

Приведем эту задачу к каноническому виду, введя допол­нительные
переменные х₃ и х₄.

max f( ) = 2 x₁ +3 x₂+ 0 х₃+0 х₄

A₁ A₂ A₃ A₄ B

,

или x₁+ 3x₂+ х₃ =300,

x₁+ x₂ +х₄ =150,

x_j0; j =.

Задача обладает исходным опорным планом (0,0,300,150), и ее можно решить симплекс-методом; решение ведется в симплекс-таблицах (табл. 3).

Таблица 3

№ симплекс-таблицы	Базис	Сб	План В	2	3	0	0	Q
A1	A2	A3	A4
0	A3	0	300	1		1	0	100
A4	0	150	1	1	0	1	150
	0	-2	-3	0	0
1	A2	3	100	1/3	1	1/3	0	300
A4	0	50	2/3	0	-1/3	1	75
	300	-1	0	1	0
2	A2	3	75	0	1	1/2	-1/2
A1	2	75	1	0	-1/2	3/2
	375	0	0	1/2	3/2

В исходной симплекс-таблице строка оценок Δ _j определяется по приведенной выше формуле

Δ ₁= z₁-c₁ =

Δ ₂ = z₂-c₂ =

Исходный опорный план (0,0,300,150) не является опти­мальным, так как среди оценок Δ _j имеются отрицательные. Переход к новому опорному плану осуществим, введя в базис вектор A₂, имеющий минимальную отрицательную оценку. Определяем вектор, выходящий из базиса:

т.е. вектор A₃ следует вывести из базиса. Направ­ляющим или ведущим элементом является a₁₂ = 3 (выделен). Переход к следующей симплекс-таблице осуществляем с по­мощью преобразований Жордана-Гаусса (первое уравнение делим на себя, затем из второго вычитаем первое).

Определим текущее значение функции и оценки. Среди оценок также имеется отрицательная, следовательно и второй опорный план (0,100,0,50) не оптимальный.

Определим ведущий (направляющий) элемент

,

следовательно, ведущий a₂₁=2/3.

Переходим к следующему опорному плану вводя в базис вектор A₁ вместо вектора A₄.

Рассчитаем оценки. Теперь они все неотрицательные. В результате получаем оптимальный план (75,75,0,0), т.е. предприятие получит максимум прибыли в размере 375,0 тыс. руб., если выпус­тит 75 единиц продукции первого вида и 75 единиц продук­ции второго вида.

▲

СИМПЛЕКС-МЕТОД С ИСКУССТВЕННЫМ БАЗИСОМ (М-МЕТОД). Применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи ЛП, запи­санной в канонической форме.

М- метод заключается в применении правил симплекс-метода к так называемой
М-задаче. Она получается из ис­ходной добавлением к левой части системы уравнений в канонической форме исходной ЗЛП таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независи­мых векторов. В линейную форму исходной задачи добав­ляется в случае ее максимизации слагаемое, представляю­щее собой произведение числа (-М) на сумму искусственных переменных, где М — достаточно большое положительное число.

В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки Δ _j, теперь будут зависеть от «буквы М». Для сравне­ния оценок нужно помнить, что М— достаточно большое по­ложительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.

В процессе решения М -задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их вы­хода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М -задачи содержит искусственные векторы или М -задача неразрешима, то исходная задача также неразре­шима.

Путем преобразований число вводимых переменных, со­ставляющих искусственный базис, может быть уменьшено до одной.

▼

Пример. Найти максимум целевой функции:

max f( ) = 3 x₁ + x₂+ x₃

при условиях 2 x₁+ x₂ =8,

x₁+ x₂ +x₃=6,

x₁0; x₂ 0; x₃ 0

Решение. Матрица условий содержит только один единичный вектор, добавим еще один искусственный вектор (искусственную неотрицательную переменную y₁ в первое ограничение):

.

Получим следующую М -задачу: найти максимум целе­вой функции

max f( ) = 3 x₁ + x₂+ x₃ - My₁

при условиях 2 x₁+ x₂ + y₁ =8,

x₁+ x₂ +x₃=6,

x₁0; x₂ 0; x₃ 0; y₁0.

М- задачу решаем симплекс-методом. Начальный опор­ный план (0,0,6,8), решение проводим в симплекс-таблицах (табл. 4).

Таблица 4

№ симплекс-таблицы	Базис	Сб	План В	3	1	1	-М	Q
A1	A2	A3	A4
0	A4	-M	8		1	0	1	4
A3	1	6	1	1	1	0	6
	-8M+6	-2M-2	-M-1	0	0
1	A1	3	4	1	0.5	0
A3	1	2	0	0.5	1
	14	0	0	0

В начальной таблице наименьшая оценка соответствует векто­ру A₁ — он вводится в базис, а искусственный вектор (строка) A₄ из базиса выводится, так как ему отвечает наименьшее Q. Ведущий элемент a_11. Столбец, соответствующий A₄, из дальнейших симплексных таблиц вычеркивается.

Полученный новый опорный план является опорным планом исходной задачи. Для него все 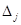> 0, поэтому он является и оптимальным. Таким образом, получен оптималь­ный план исходной задачи (4,0,2), и максимальное значение целевой функции f()=14.

▲

▼

Пример. Решить ЗЛП: min f( ) = 10 x₁ - 5x₂

при условиях 2 x₁ - x₂ 3,

x₁+ x₂ 2,

x₁+2x₂ -1,

x₁0; x₂ 0;

Приведем ЗЛП к каноническому виду, перейдя к задаче «на максимум»:

mах f₁( ) = -10 x₁ + 5x₂

при условиях 2 x₁ - x₂ - x₃=3,

x₁+ x₂ – x₄=2,

-x₁ - 2x₂ +x₅=1,

x_j0; j =.

Для нахождения опорного плана переходим к М -задаче:

mах g( , 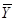) = -10 x₁ + 5x₂ –M(y₁₊ y₂)

при условиях 2 x₁ - x₂ - x₃₊ y₁=3,

x₁+ x₂ – x_{4 +} y₂=2,

-x₁ - 2x₂ +x₅=1,

x_j0; j =, y_1,20

Дальнейшее решение проводим в симплекс-таблицах (табл.5).

В симплекс-таблице 2 получен опорный план исходной ЗЛП; поскольку все оценки 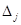> 0, то этот план явля­ется и оптимальным, т.е. x₁= 5/3, x₂ = 1/3 (исходные
перемен­ные), x₅ = 10/3, x₃ = 0, x₄ = 0 (дополнительные переменные), при этом
min f( ) = - mах f₁( ) = -(-15) = 15.

Таблица 5

№ симплекс-таблицы	Базис	Сб	План В	-10	5	0	0	0	-M	-M	Q
A1	A2	A3	A4	A5	A6	A7
0	A6	-M	3		-1	-1	0	0	1	0	3/2
A7	-M	2	1	1	0	-1	0	0	1	2
A5	0	1	-1	-2	0	0	1	0	0	-
	-5M	-3M+10	-5	M	M	0	0	0
1	A1	-10	3/2	1	-1/2	-1/2	0	0		0
A7	-M	1/2	0	3/2	1/2	-1	0	1	1/3
A5	0	5/2	0	-5/2	-1/2	0	1	0
	-M/2-15	0	-3M/2	-M/2+5	M	0		0
2	A1	-10	5/3	1	0	-1/3	-1/3	0
A2	5	1/3	0	1	1/3	-2/3	0
A5	0	10/3	0	0	0	-5/3	1
	-15	0	0	5	0	0

▲

Дата добавления: 2014-01-14