Симплекс метод

Методы линейного программирования

Графический способ решения озлп показывает, что решение этой задачи всегда ассоциируется с узловой точкой пространства решений. В математике эта точка называется крайней точкой множества. Переход от геометрического способа решения озлп лежит через алгебраическое описание крайних точек пространства решений.

Для реализации перехода приведем сначала к стандартной форме, используя знаки <, >, = и далее базисные решения (x₁,x₂), получаемые из стандартной формы, будут полностью определять все крайние точки пространства решений. Таким образом, симплекс-метод помогает оптимальное решение среди базисных.

Определение базисных решений

ОУЛП содержит m линейных равенств с n неизвестными переменными, причем m<n. Разделим n переменных на 2 множества. 1ое будет определяться из условия n - m = 0. Оставшиеся переменные определяются как решения системы из m линейных уравнений. Если это решение единственное, то переменные являются базисными. Оно будет допустимым, если все переменные принимают неотрицательные значения. Количество всех положительных базисных решений для m уравнений с n неизвестными не превосходит по величине:

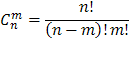
Алгоритм симплекс-метода

Данный алгоритм находит оптимальное решение, рассматривая ограниченное количество допустимых базисных решений. Он находит базисное решение 1-первоначальное- и, затем, пытается найти другое допустимое, улучшающее значение целевой функции. Это возможно в случае, если увеличение небазисной переменной ведет к улучшению значения целевой функции. Но, в этом случае, одну из базисных переменных надо заменить => эту переменную мы «зануляем», чтобы, может быть, потом на её место поставить другую; ту, которую удаляем – исключаемая переменная, ту, которую заменяем – вводимая.

Связь между min и max max z = - min (-z)

В зависимости от того, max-ем или min-ем, мы выбираем отрицательные или положительные переменные.

Если min-ем, вводимая переменная выбирается как небазисная с наибольшим положительным коэффициентом в z строке симплекс-таблицы, а min целевой функции будет достигнут тогда, когда все коэффициенты в z строке будут положительными.

2 условия выбора вводимых и исключаемых переменных в симплекс-методе:

1. Условие оптимальности: вводимой переменной в задаче max-ии (min-ии) выбирается небазисная переменная, имеющая наибольший отрицательный (положительный) коэффициент в z строке симплекс-таблицы. Если несколько одинаковых значений, то выбираем произвольно. => оптимальное решение будет достигнуто тогда, когда в z строке все коэффициенты при небазисных переменных будут неотрицательны (неположительны)

2. Условие допустимости: в задачах max-ии (min-ии) в качестве исключаемой переменной выбирается базисная, для которой отношение значения правой части ограничения к положительному коэффициенту ведущего столбца минимально. Если базисных переменных несколько – выбор произволен.

Последовательность действий:

1. Находим начальное допустимое базисное решение

2. На основе условия оптимальности определяется вводимая переменная. Если нет, то всё.

3. На основе условия допустимости выбираем исключаемую переменную

4. Методом Гаусса-жордана выбирается новое базисное решение

5. Переходим к п.2

Все вычисления проводятся нами операционно и совокупность получаемых симплекс-таблиц – это итерация.

Задача:

Есть целевая функция z = 5x₁ + 4x₂, которую надо max-ть

Есть краска: x₁ для наружных работ, от неё прибыль в 5$; x₂ для внутренних работ, от неё прибыль в 4$

6x₁ + 4x₂ + s₁ = 24 s_i – добавляемые переменные для получения рав-в

x₁ + 2x₂ + s₂ = 6

-x₁ + x₂ + s₃ = 1

x₂ + s₄ = 2

с учетом s₁…s_n целевая функция получает новый вид:

z = 5x₁ + 4x₂ + 0×s₁ + 0×s₂ + 0×s₃ + 0×s₄

z-строка в симплекс-таблице

z -5x₁ - 4x₂ - 0×s₁ - 0×s₂ - 0×s₃ - 0×s₄ = 0

Симплекс-таблица (*)

Базис	z	x1	x2	s1	s2	s3	s4	решение
z		-5	-4
s1
s2
s3		-1
s4

Определение исключаемой переменной:

базис	x1	решение
s1			24/6=4 => min коэфф.
s2			6/1=6
s3	-1		1/-1 - отриц
s4			2/0 – нельзя ÷ на ноль

Вычисление нового базисного решения (s1↔x1)

1. Вычисление элементов новой ведущей строки

н.в.с. =

(*) s₁ 0 6/6 4/6 1/6 0/6 0/6 0/6

2. Остальные строки

новая строка = текущая – (её коэфф в ведущей строке)×(н.в.с.)

zтекущ		-5	-4
(-5)×(н.в.с.)			10/3	5/6
			-2/3	5/6

Аналогично s₁ s₂ s₃ s₄

Базис	z	x1	x2	s1	s2	s3	s4	решение
z			-2/3	5/6
x1			2/3	1/6	0/6	0/6	0/6
s2			4/3	-1/6
s3			5/3	1/6
s4

z = x₂ - 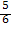s₁ + 20

	x2	решение
x1	2/3		4/(2/3) = 6
s2	4/3		2/(4/3) = 1.5
s3	5/3		5/(5/3) = 3
s4			2/1 = 2

Пз: 3^ю симплекс-таблицу.

В z строке в графе решение должно получится 21

н.в.с = 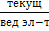= 0 0 1 -1/6 ¾ 0 0 │3/2

н.с. = текущ – (её коэфф в вед столбце)×н.в.с.

z → -2/3

x₁ → 2/3

s₃ → 5/3

s₄ → 1

Базис	z	x1	x2	s1	s2	s3	s4	решение
Z				¾	½
x1				¼	-½
x2				-1/8	¾			3/2
s3				3/8	-5/4			5/2
s4				1/8	-¾			½

Из конечной симплекс таблицы можно получить следующую информацию:

1. Узнать о состоянии ресурсов

2. Оптимальную цену единицы ресурса

3. Данные для проведения анализа чувствительности оптимального решения

Статус ресурса можно определить как дефицитный или нет, то есть, будет ли он использован полностью или же что-то останется, для этого мы проверим остаточные переменные и, если они будут равны 0, то ресурс использован полностью.

s₃,s₄ – спросы

в s₃ будет недостаток 5/2 тонн, в s₄ будет недостаток ½ => нужно будет увеличить x₁ на 2,5т, а x₂ – на 0,5т

s₁(x₁) = 0; s₂(x₂) = 0; s₃(x₁) = 5/2т; s₄(x₂) = ½т

Дата добавления: 2014-01-14