Особенности матрицы перехода

1. Каждая строка характеризует выбранное состояние системы, а её элементы представляют собой вероятности всех возможных переходов за один шаг из выбранного (из 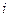-го) состояния, в том числе и переход в самое себя.

2. Элементы столбцов показывают вероятности всех возможных переходов системы за один шаг в заданное (в -е) состояние.

Другими словами, строка характеризует вероятность перехода системы из состояния, а столбец – в состояние.

3. Сумма вероятностей каждой строки равна единице, так как переходы образуют полную группу несовместных событий:

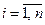, . (4.4)

4. По главной диагонали матрицы переходных вероятностей стоят вероятности 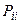того, что система не выйдет из состояния 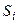, а останется в нём.

Теорема 4.1. Если для однородной марковской цепи заданы начальное распределение вероятностей (4.2) и матрица переходных вероятностей 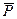(4.3), то вероятности состояний системы на -м шаге 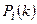(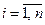) определяются по рекуррентной формуле:

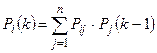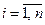(,). (4.5)

Замечание. Если начальное распределение вероятностей, распределение вероятностей на -м шаге и распределение вероятностей на -м представить в виде вектор-столбцов , , соответственно, то рекуррентную формулу (4.5) можно записать в эквивалентной матричной форме:

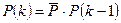, (4.5’)

а вектор распределения вероятностей на -м шаге можно вычислить по формуле:

, (4.6)

Пример 4.1. Пусть автомобиль (система) в течение одной смены (суток) может находиться в одном из двух состояний: исправном (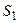) и неисправном (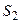). В результате массовых наблюдений за работой автомобиля было выявлено, что в течение суток в 80% случаев автомобиль останется исправным, в 20% случаев сломается, в 90% случаев неисправный автомобиль починят, в 10% случаев поломку устранить не смогут. В начальный момент времени автомобиль был неисправен. Требуется:

1) построить граф состояний системы;

2) составить матрицу вероятностей перехода;

3) определить вероятности состояний автомобиля через трое суток.

Решение. 1) Построим граф состояний системы «автомобиль». Так как система «автомобиль» имеет два состояния 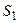– исправен и 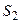– неисправен, причём в каждом из состояний она может как задержаться, так и перейти в другое состояние, то граф состояний системы будет иметь:

две вершины – состояния 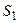и ;

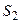петли в каждой вершине; петли характеризуют тот факт, что система может задержаться в каждом из состояний;

две дуги, соединяющие эти вершины, и характеризующие переход из одного состояния в другое (см. рис. 4.2).

2) Составим матрицу вероятностей перехода.

Так как в течение суток в 80% случаев автомобиль останется исправным, то – вероятность того, что автомобиль останется в исправном состоянии.

Так как в течение суток в 20% случаев автомобиль сломается, то – вероятность того, что автомобиль перейдёт из состояния «исправен» в состояние «неисправен».

Так как в течение суток в 90% случаев неисправный автомобиль починят, то – вероятность того, что автомобиль перейдёт из состояния «неисправен» в состояние «исправен».

Так как в течение суток в 10% случаев поломку устранить не смогут, то – вероятность того, что автомобиль задержится в состоянии «неисправен». Таким образом, матрица вероятностей перехода примет вид: .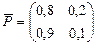

3) Найдём распределение вероятностей состояний автомобиля через трое суток (). Так как в начальный момент времени автомобиль был неисправен, то , и начальное распределение вероятностей автомобиля имеет вид: . Тогда по формуле (4.6) имеем

.

Ответ. После третьих суток автомобиль будет находиться в исправном состоянии с вероятностью 0,819 и в состоянии «неисправен» с вероятностью 0,181.

Дата добавления: 2014-01-14