Финальные вероятности состояний

Если процесс, протекающий в системе, длится достаточно долго, то рассматривают предельное поведение вероятносте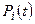й при .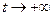

Определение 6. Финальной (предельной) вероятностью состояния 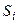(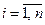) называется предел ().

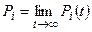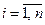Замечание. Финальные вероятности состояний не зависят от того, в каком состоянии система S находилась в начальный момент. В этом случае говорят, что в системе S устанавливается предельный стационарный режим, в ходе которого она переходит из состояния в состояние, но вероятности состояний 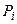уже не меняются. Система, для которой существуют финальные вероятности, называется эргодической системой, а соответствующий случайный процесс – эргодическим процессом.

Так как финальные вероятности состояний характеризуют установившийся процесс, то для всех 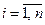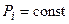, а 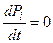. Поэтому финальные вероятности состояний (если они существуют) могут быть получены путём решения системы линейных алгебраических уравнений, которые получаются из дифференциальных уравнений Колмогорова, если приравнять производные нулю, а вероятностные функции состояний 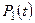, , 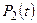…, 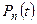в правых частях уравнений (4.8) заменить соответственно на неизвестные финальные вероятности , , …, :

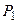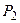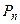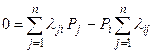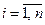, . (4.9)

Так как система (4.9) является линейной однородной алгебраической системой, то (см. например [2, с. 238]), то неизвестные финальные вероятности (при условии, что они существуют и отличны от нуля) можно найти с точностью до произвольной постоянной. Для нахождения точных значений 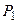, , 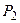…, 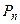к уравнениям (4.9) добавляют так называемое нормировочное условие 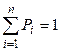, пользуясь которым можно выразить любую вероятность 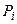через другие.

Замечание. Если 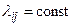(процесс однородный), то финальные вероятности существуют всегда, но могут быть равны нулю. Для того, чтобы финальные вероятности однородного процесса были отличны от нуля, необходимо и достаточно, чтобы ранг системы (4.9) был меньше числа неизвестных этой системы (см. например [2, с. 238]).

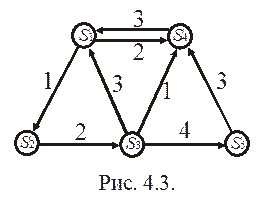Пример 4.2. Имеется размеченный граф состояний системы S (см. рис. 4.3). Требуется:

1) составить систему дифференциальных уравнений Колмогорова;

2) записать начальные условия для решения этой системы, если известно, что в начальный момент времени система находилась в состоянии ;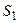

3) найти финальные вероятности состояний системы.

Решение. 1) Составим систему уравнений Колмогорова в общем виде.

Для состояния 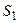первое уравнение, согласно мнемоническому правилу, будет иметь вид:

Так как

Аналогично рассуждая, получим остальные уравнения системы в общем виде:

Подставляя в систему значения 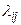, указанные на графе, получим:

Замечание. При решении задач необязательно составлять систему уравнений Колмогорова сначала в общем виде, т.е значения 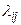, указанные на графе, можно подставлять сразу.

2) Так как в начальный момент времени система находилась в состоянии 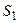, то начальные условия при 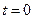примут вид:

3) Найдём финальные вероятности состояний. Для этого приравняем производные нулю, а вероятностные функции состояний 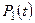, , 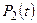…, 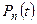в правых частях уравнений (4.8) заменим соответственно на неизвестные финальные вероятности , , …, :

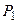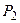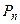Решим полученную систему линейных алгебраических уравнений методом Гаусса:

Учтём условие нормировки:

Тогда можно вычислить все финальные вероятности состояний:

Дата добавления: 2014-01-14