Полярная система координат на плоскости

Определение. Полярной системой координат на плоскости называется точка 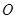и числовой луч с заданной единицей масштаба.

Точка 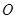называется полюсом, луч - полярной осью.

На рисунках полярную ось располагают горизонтально и направленной слева направо.

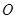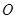Возьмем на плоскости точку , не совпадающую с точкой . Положение точки определяется двумя величинами: ее расстоянием от точки полюса и углом , образованным лучом и отрезком . Полярный угол считается положительным при отсчете от полярной оси против часовой стрелки о отрицательным, если по часовой стрелки.

Числа и называются полярными координатами точки и пишут , при этом называется полярным радиусом точки , а - полярным углом точки .

Для получения всех точек плоскости достаточно, чтобы 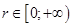, а (или ).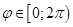

Две величины и полностью и однозначно определяют положение точки (кроме точки 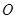) на плоскости, а именно: каждой паре величин и соответствует единственная точка на плоскости и наоборот.

Установим связь между прямоугольной декартовой и полярной системой координат на плоскости.

Для этого совместим полюс 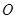с началом координат системы , а полярную ось - с положительной полуосью оси 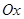. Пусть и 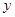- прямоугольные декартовые координаты точки , а и - ее полярные координаты.

Из полученного рисунка видно, что прямоугольные декартовые координаты точки выражаются через ее полярные координаты следующим образом:

Полярные же координаты точки выражаются через ее прямоугольные декартовые координаты следующим образом:

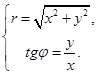
В последней системе заметим, что при нахождении угла следует установить по знакам и 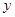четверть, в которой лежит искомый угол, и учитывать, что .

Например, Дана точка 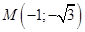. Найти полярные координаты точки .

Решение: Воспользуемся системой 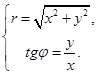, т.е. .

Так как точка лежит в четверти, то .

Итак, .

Некоторые приложения метода координат на плоскости.

1. Расстояние между двумя точками.

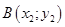Расстояние между двумя точками и на плоскости находится по формуле:

.

2. Деление отрезка в данном отношении.

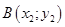Пусть даны две точки и на плоскости . Пусть через них проходит некоторая прямая .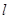

Где бы не находилась точка на прямой 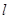, будем говорить что она делит отрезок в отношении , если выполняется равенство .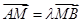

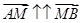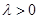Если , то и деление отрезка в данном случае называется внутренним (точка принадлежит отрезку ), при этом , .

Если , то и деление отрезка в данном случае называется внешним (точка не принадлежит отрезку ), при этом , .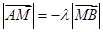

Так как и , то

Таким образом, - формулы нахождения координат точки , которая делит отрезок в данном отношении (формулы деления отрезка в данном отношении).

Если , т.е. точка делит отрезок пополам, то координаты точки находятся по формулам:

3. Площадь треугольника.

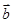
Пусть даны три точки , 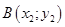и на плоскости . Требуется найти площадь треугольника, образованными этими тремя точками, т.е. .

Напомним формулу нахождения площади треугольника, образованного двумя векторами и 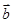: , причем .

Если вектора и 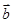лежат на плоскости , как в нашей задаче, то их координаты и 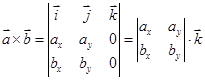. Отсюда .

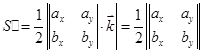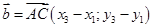Так как и , то

.

Данная формула является формулой нахождения площади треугольника на плоскости, заданного координатами трех своих вершин , 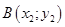и .

Контрольные вопросы:

1. Сформулируйте определение системы координат на плоскости.

2. Сформулируйте определение прямоугольной декартовой системы координат на плоскости.

3. Сформулируйте определение полярной системы координат на плоскости.

4. Какими формулами связаны координаты точки в прямоугольной декартовой и полярной системе координат?

5. Как найти расстояние между двумя точками на плоскости?

6. Запишите формулы деления отрезка в данном отношении.

7. Как найти площадь треугольника на плоскости, заданного координатами трех своих вершин?

Дата добавления: 2014-01-14