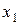Непрерывность функции в точке и на отрезке.

Функция y=f(x) называется непрерывной в точке х₀, если выполняются условия:

1) функция определена в точке ;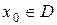

2) существует предел функции ;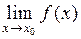

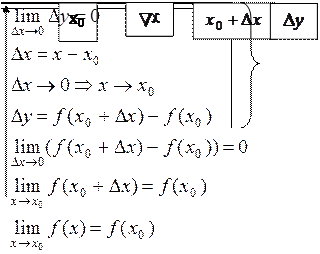3)

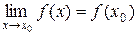
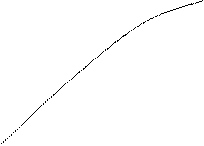Геометрически непрерывность функции в данной точке означает, что разность ординат графика в точках с абсциссами х₀, х₀+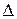х будет б.м. по величине.

Теорема 1. Если f₁(x) и f₂(x) непрерывны, то f₁(x)+f₂(x) непрерывна в точке х₀.

Доказательство:

Опираясь на свойства пределов, можно доказать следующую теорему о функциях, непрерывных в точке х₀.

Теорема 2. Произведение двух непрерывных функций есть функция непрерывная, если значение не обращается в нуль.

В силу теорем 1-3 многочлен является непрерывной функцией.

Дробно-рациональная функция непрерывна во всех х, если знаменатель не обращается в нуль.

Теорема 3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель не обращается в нуль.

Теорема 4. Если функция непрерывна в точке х₀, а t(u) непрерывна , то 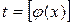непрерывна в точке х₀.

Пример: 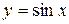- непрерывна.

Теорема 5. Если y=t(x) непрерывна и строго монотонна на промежутке (a, b), то существует обратная функция , определяемая на промежутке [t(a), t(b)], также непрерывная и монотонная.

Всякая элементарная функция непрерывна в каждой точке, где она определена.

Если y=t(x) непрерывна в каждой точке некоторого интервала АВ (A<B), то говорят, что она непрерывна на этом интервале.

Если 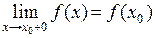, то f(x) непрерывна справа. Если , то f(x) непрерывна слева. Если функция непрерывна и слева, и справа, то она непрерывна в точке х₀. Если функция непрерывна в каждой точке интервала АВ и непрерывна на концах (в точке А справа, а в точке В слева), то функция непрерывна на отрезке АВ.

Определение и классификация точек разрыва

Если в какой-либо точке х=х₀ для y=f(x) не выполняется по крайней мере одно из условий 1-3, т.е. если в точке х=х₀ функция не определена, не существует предел функции при хх₀ и 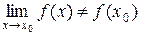, то при х=х₀ функция имеет разрыв.

Опр. Точка х₀ называется точкой разрыва функции y=f(x), если f(x) в точке х₀ не является непрерывной.

Разрывность функции классифицируется следующим образом:

1. Точка разрыва первого рода – если пределы

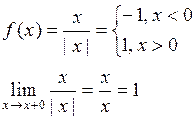
Если х₀ – точка разрыва I-го рода, то скачком функции называется разность ,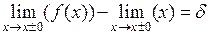

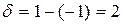
Точка разрыва I-го рода называется точкой устранимого разрыва, если в ней предел справа равен пределу слева.

2. Точка разрыва второго рода. Точка х_-0 называется точкой разрыва второго рода, если в этой точке функция не имеет по крайней мере одного предела или хотя бы один из них равен бесконечности.

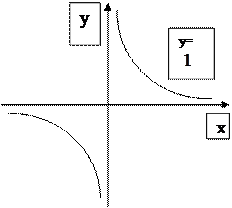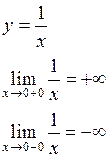
Свойства непрерывности функций.

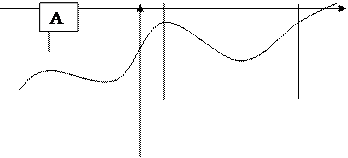Теорема 1. Если f(x) непрерывна на АВ, то она достигает на этом отрезке хотя бы один раз своего наименьшего значения m и наибольшего значения М. f(x₁)=m, f(x₂)=M.

Следствие: Если f(x) непрерывна на [a, b], то она ограниченна на этом отрезке.

Теорема 2. Пусть f(x) непрерывна на [a, b] и на концах этого отрезка принимает

значения разных знаков, тогда между a и b найдется a<c<b, в которой функция f(x) обращается в нуль.

Теорема 3. П усть y=f(x) определена и непрерывна на [a, b] и на концах отрезка принимает неравные значения f(a)=A, f(b)=B, тогда каково бы ни было A<C<B, найдется такая точка х=c, a<c<b, что f(c)

=C. Прямая у=с, где A<C<B, пересекает график по крайней мере в одной точке.

Непрерывная функция, переходя от одного значения к другому, проходит через все его промежуточные значения.

Замечание: если функция имеет на отрезке хотя бы одну точку разрыва, то утверждение теорем 2 и 3 перестает быть верным.

Следствие теоремы 3: если f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает хотя бы один раз любое значение, заключенное между наибольшим и наименьшим.

Гиперболические функции. Их графики. Соотношения между ними.

shx – гиперболический синус

chx – гиперболический косинус

thx – гиперболический тангенс

cthx – гиперболический котангенс

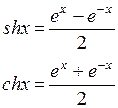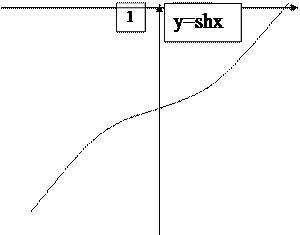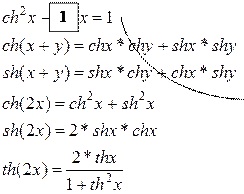Дата добавления: 2014-01-14