Статически неопределимые системы

18.1. Общие понятия и определения

Статически неопределимая система – это конструкция, силовые факторы в элементах которой невозможно определить только из уравнений равновесия (уравнений статики).

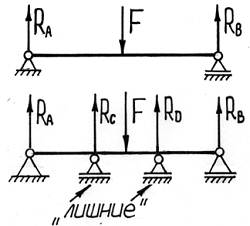Статическая неопределимость возникает в том случае, когда число наложенных на систему связей оказывается больше, чем это необходимо для обеспечения ее равновесия. При этом некоторые из этих связей становятся как бы «лишними», а усилия в них – лишними неизвестными. По числу лишних неизвестных устанавливают степень статической неопределимости системы. Отметим, что термин «лишние» связи является условным, так как эти связи необходимы для обеспечения прочности и жесткости системы, хотя и «избыточны» с точки зрения ее равновесия.

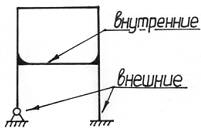Связь – условие закрепления или соединения элементов конструкции, не допускающее изменения их взаимного положения (внутренние связи) и положения в пространстве (внешние связи).

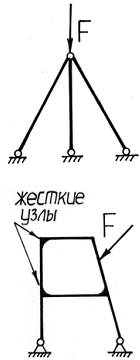До сих пор мы рассматривали простейшие статически неопределимые системы, элементы которых работали только на растяжение (сжатие). Такие конструкции обычно называют фер м ами. Ферма – конструкция, состоящая из прямых стержней, соединенных между собой шарнирами, и нагруженная силами, приложенными в узлах (в шарнирах).

Далее рассмотрим более общие случаи статически неопределимых систем, элементы которых могут находиться в условиях сложного сопротивления, испытывать изгиб, кручение и т. д. Наиболее распространенным примером таких конструкций являются рамы.

Рама – конструкция, состоящая из стержней произвольной конфигурации и имеющая один или несколько жестких (не шарнирных) узлов.

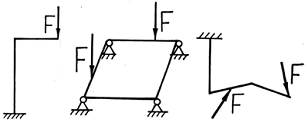Как рамы, так и фермы могут быть а) плоскими – все элементы конструкции и силы лежат в одной плоскости; б) плоскопространственными – все элементы конструкции лежат в одной плоскости, а силы перпендикулярны к этой плоскости; в) пространственными – элементы конструкции и силы располагаются произвольно друг относительно друга.

Для раскрытия статической неопределимости необходимо, помимо статической стороны задачи, проанализировать деформации системы и в дополнение к уравнениям равновесия составить уравнен ия совместности де формац ий, из решения которых и находятся «лишние» неизвестные. При этом число таких уравнений должно равняться степени статической неопределимости системы.

В общем случае нагружения статически неопределимой системы наиболее эффективными способами определения деформаций ее элементов являются энергетические методы, возможности применения которых рассмотрим в следующем параграфе.

18.2. Метод сил. Основная идея метода

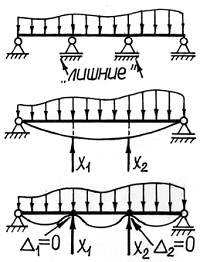Для того чтобы обратить заданную статически неопределимую систему в статически определимую, в методе сил используется следующий прием. Все «лишние» связи, наложенные на конструкцию, отбрасываются, а их действие заменяется соответствующими реакциями – силами или моментами. При этом, для сохранения заданных условий закрепления и нагружения, реакции отброшенных связей должны иметь такие значения, при которых перемещения в направлении этих реакций равнялись бы нулю (или заданным величинам).

Таким образом, при раскрытии статической неопределимости этим методом

искомыми оказываются не деформации, а соответствующие им силы – реакции связей (отсюда и название «метод сил»).

Запишем основные этапы раскрытия статической неопределимости по методу сил:

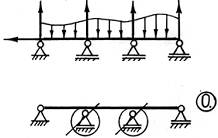1) определяем степень статической неопределимости системы, то есть число лишних неизвестных;

2) удаляем лишние связи и заменяем таким образом исходную статически неопределимую систему статически определимой. Эта новая система, освобожденная от лишних связей, называется основной.

Заметим, что выбор лишних связей может быть достаточно произвольным и зависит лишь от желания расчетчика, так что для одной и той же исходной статически неопределимой системы возможны различные варианты основных систем. Однако нужно следить за тем, чтобы основная система оставалась геометрически неизменяемой – то есть ее элементы после удаления лишних связей не должны иметь возможности свободно перемещаться в пространстве.

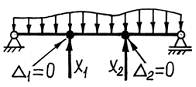3) составляем уравнения для деформаций в точках приложения лишних неизвестных. Так как в исходной системе эти деформации равны нулю, то и указанные уравнения необходимо также приравнять к нулю. Затем из полученных уравнений находим величину лишних неизвестных.

18.3. Канонические уравнения метода сил

Определять перемещения соответствующих точек основной системы можно любым способом, однако лучше всего общими методами – методом Максвелла-Мора или способом Верещагина. При этом дополнительные уравнения перемещений удобно составлять в так называемой канонической фор м е, то есть по определенной закономерности.

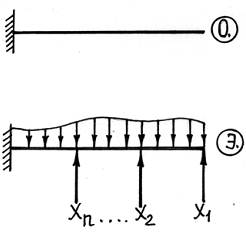
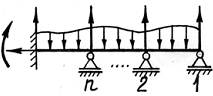Рассмотрим балку, загруженную произвольной системой сил, на которую наложено n «лишних» связей – система n раз статически неопределима.

Для раскрытия статической неопределимости используем метод сил.

1) Освободим балку от лишних связей и получим вид основной системы. Далее все рассуждения будем проводить применительно к основной системе.

2) Загрузим основную систему всеми внешними силами, а также лишними неизвестными в местах расположения и в направлении отброшенных связей (X1, X2,…, Xn). Полученную систему будем называть эквивалентной.

Эквивалентная система – система, полученная из основной, после ее загрузки внешними силами и лишними неизвестными.

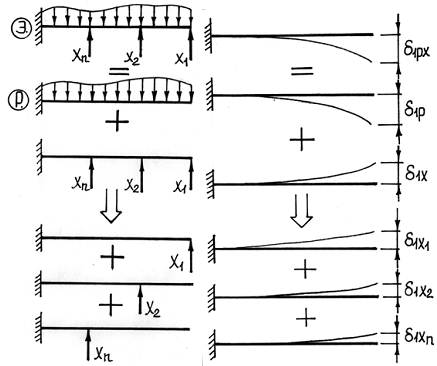3) Рассмотрим деформации эквивалентной системы (например, в точке 1). Под действием внешних нагрузок (P) и лишних неизвестных (X) точка 1 сместится на некоторую величину δ1PX. Согласно принципу независимости действия сил, эта деформация может быть найдена как сумма двух деформаций – деформации балки только под действием внешних сил δ1P и деформации балки под действием лишних неизвестных δ1X

Проанализируем перемещение δ1X точки 1 под действием лишних неизвестных (X1, X2,…, Xn). Каждая из лишних неизвестных (X1, X2,…, Xn) сама по себе вызовет некоторую деформацию балки 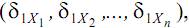при этом сумма таких деформаций и составит в итоге полную деформацию балки от лишних неизвестных

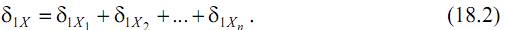
Для определения деформаций 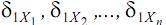используем следующий искусственный прием. Приложим к основной системе вместо лишних неизвестных (X1, X2,…, Xn) известные единичные силы (силы, величина которых равна единице), обозначим их 1, 2, 3,…, n.

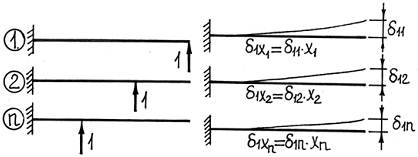Каждая единичная сила в отдельности сдеформирует балку на некоторую величину (δ11, δ12,…, δ1n). Так как неизвестная X1 отличается от единичной силы 1 в X1 раз, то и деформации, вызванные этими силами, будут отличаться в X1 раз в силу линейной связи (закон Гука!) между деформациями и усилиями, то есть

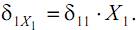
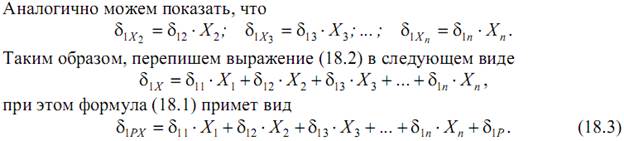
4) Так как в точке 1 исходной системы была установлена опора (лишняя связь), то для сохранения эквивалентности исходной и рассматриваемой систем необходимо потребовать, чтобы перемещение в этой точке равнялось нулю, то есть δ1PX=0, или, с учетом (18.3)

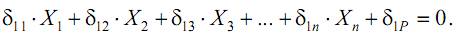
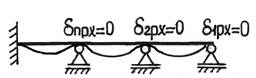Подобные рассуждения можем провести для каждой точки исходной системы, где установлена опора (лишняя связь). В итоге получим следующую систему уравнений:

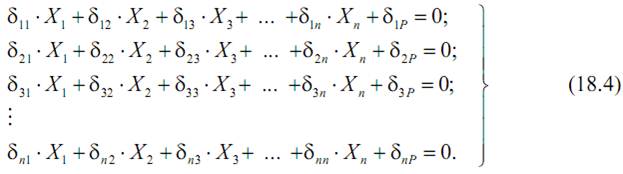
Это и есть система канонических уравнений метода сил. Она содержит n уравнений с n неизвестными «лишними» силами (X1, X2,…, Xn), которые и найдем, решая систему (18.4).

5) Определим коэффициенты δ, входящие в уравнения (4).

Коэффициент δiP есть перемещение i-ой точки основной системы под действием внешних сил (P). Для его определения можно воспользоваться методом Максвелла-Мора, учитывая все участки конструкции

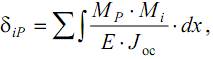
где MP – внутренний изгибающий «грузовой» момент (определяется по «грузовой» системе, то есть системе, нагруженной только внешними силами); Mi – внутренний изгибающий «единичный» момент (определяется по «единичной» системе, то есть системе, нагруженной только единичной силой, приложенной в i-ой точке).

Коэффициент δij есть перемещение i-ой точки основной системы под действием j-ой единичной силы. Для его определения можно также воспользоваться методом Максвелла-Мора с учетом всех участков системы

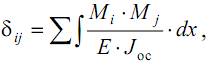
где Mi – внутренний изгибающий «единичный» момент (определяется по i-ой «единичной» системе, то есть системе, нагруженной только единичной силой, приложенной в i-ой точке); Mj – внутренний изгибающий «единичный» момент (определяется по j-ой «единичной» системе, то есть системе, нагруженной только единичной силой, приложенной в j-ой точке).

Таким образом, для определения коэффициентов δ необходимо определить внутренние изгибающие моменты для нескольких систем: одной «грузовой», загруженной только внешними силами, и несколькими «единичными», каждая из которых загружается всего лишь одной силой – единичной силой, приложенной по направлению и в той точке, где ищется лишняя неизвестная (X). Затем эти внутренние усилия необходимо подставить в интеграл Максвелла-Мора и найти δ.

18.4. Учет симметрии при расчете статически неопределимых систем

Можно значительно упростить систему канонических уравнений метода сил, если есть возможность учесть симметрию конструкции и приложенных к ней нагрузок, поскольку при этом некоторые побочные коэффициенты канонических уравнений оказываются равными нулю.

Симметричной будем называть конструкцию, если одна из ее частей является зеркальным отражением второй части относительно плоскости (оси) симметрии.

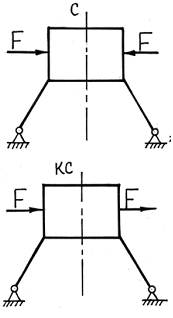Усилия (и внешние, и внутренние), действующие на симметричную конструкцию, можно разделить на симметричные и кососимметричные.

Симметричной будем считать нагрузку, если усилия, приложенные к одной части конструкции, являются зеркальным отображением усилий, приложенных к другой ее части.

Кососимметричной будем считать нагрузку, если усилия, приложенные к одной части конструкции, являются зеркальным отображением усилий, приложенных к другой ее части, но взятых с противоположным знаком.

Заметим, что любую несимметричную нагрузку, приложенную к симметричной конструкции, можно разложить на две составляющие, одна из которых будет симметричной, а другая – кососимметричной. Полученные две задачи решаются затем с учетом симметрии, а результаты суммируются.

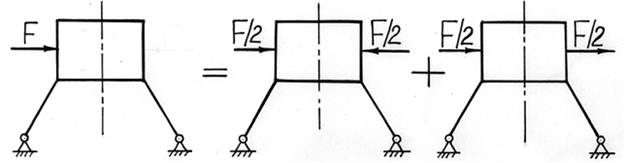
Особенностью, упрощающей решение статически неопределимых задач с учетом симметрии, является тот факт, что в качестве лишних неизвестных здесь целесообразно выбирать не реакции опор, а внутренние усилия, расположенные в плоскости симметрии конструкции.

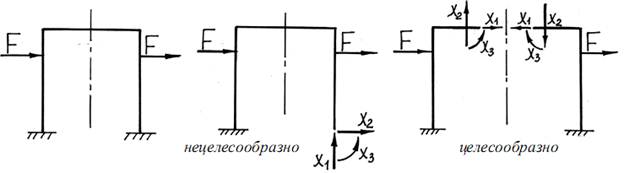
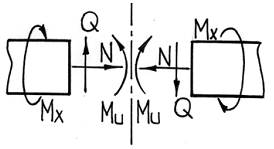При этом искомые внутренние усилия можно будет также подразделить на симметричные и кососимметричные: осевое усилие N и изгибающие моменты My, Mz – симметричные силовые факторы, а поперечные силы Qy, Qz и крутящий момент Mx –кососимметричные.

При анализе симметричных конструкций удобно использовать следующие правила:

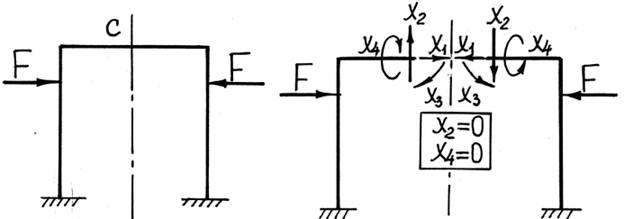
1) в симметричной конструкции при симметричной внешней нагрузке в плоскости симметрии равны нулю кососимметричные внутренние усилия (Q, Mx);

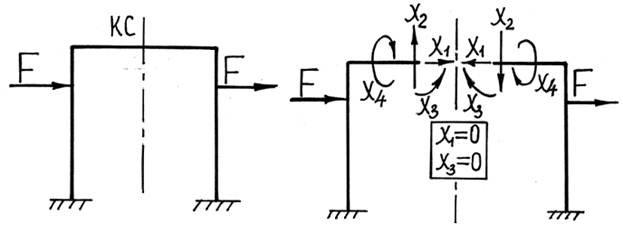
2) в симметричной конструкции при кососимметричной внешней нагрузке в плоскости симметрии равны нулю симметричные внутренние усилия (N, My, Mz).

После того как путем решения системы канонических уравнений найдены неизвестные «лишние» усилия X1, X2,…, Xn, эти усилия и заданную нагрузку можно приложить к основной системе (получим эквивалентную статически определимую систему). Затем от их совместного действия обычным способом можно определить внутренние усилия по участкам системы, построить их эпюры и провести расчет на прочность.

Дата добавления: 2014-01-14