Многочлена с действительными коэффициентами на линейные и квадратные многочлены

Основная теорема алгебры. Разложение

Теорема: Всякий многочлен степени 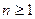имеет, по крайней мере, один действительный комплексный корень.

Замечание: То, что в теореме говорится о многочлене, существенно. Неалгебраическое уравнение может не иметь ни действительных, ни комплексных корней. Например: е^х = 0.

Действительно, при любом комплексном х = α +iβ

.

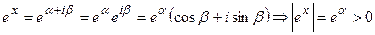Следствие: Многочлен 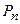(x) степени n имеет n корней с учётом их кратности, т.е. представим в виде произведения:

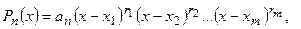(12)

где x ₁, x ₂, …x_m – различные корни многочлена 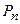(x) кратности r ₁, r ₂, … r _m (r ₁ +r ₂ +…+r_m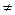n). Некоторые (или все) корни могут быть комплексными.

Доказательство:

По основной теореме многочлен имеет хотя бы один корень. Обозначим его через х, а его кратность через r ₁. Тогда по формуле (11):

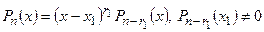
Если r ₁ = n, то 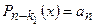и 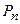(x)=(х-х ₁) ⁿa_n и теорема доказана.

Если r ₁ <n и к многочлену степени n – r ₁, 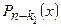снова применяем основную теорему. Обозначим корень этого многочлена через х ₂, а его кратность через r ₂. В результате получим:

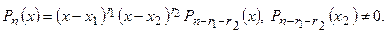
Процесс закончится через конечное число шагов (не большего n) и мы придем к формуле (12).

Если в правую часть (12) подставить вместо х число, отличное от x ₁, x ₂, …x_m, то она не обратится в нуль. Это показывает, что других корней, кроме найденных, многочлен P_n (x) не имеет и представление (12) единственно.

Все сказанное до сих пор относится к многочленам как с действительными, так и с комплексными коэффициентами. Пусть теперь многочлен P_n (x) имеет действительные коэффициенты и пусть у него имеется комплексный корень кратности s:

x_k = α + iβ.

Оказывается, что если коэффициенты действительны, то и число 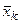= α - iβ тоже будет корнем той же кратности.

Т.е. в этом случае комплексные корни многочлена являются комплексно – сопряжёнными.

Рассмотрим множители:

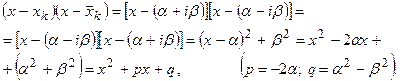
Следовательно, объединяя скобки, соответствующие комплексно - сопряженными корнями в выражении (12), многочлен степени n с действительными коэффициентами можно разложить только на действительные множители – линейные и квадратичные:

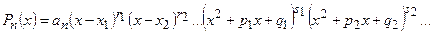
где, все трёхчлены не имеют действительных корней.

Если многочлен не имеет комплексных корней, то квадратичные множители будут отсутствовать.

Пусть имеется дробно -рациональная функция R (x):

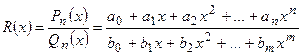
Если n < m, то дробь правильная. Если 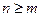, то неправильная. Неправильную дробно-рациональную функцию путём деления числителя на знаменатель всегда можно представить, в виде суммы многочлена и правильной рациональной дроби:

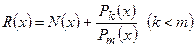
Оказывается, как увидим позже, всякую правильную дробно – рациональную функцию можно представить в виде суммы простейших дробно-рациональных функций четырёх типов.

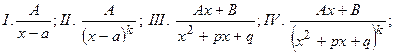
где A, B, р, q – действительные числа, а трёхчлен x ² + px + q не имеет действительных корней, т.е. .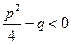

Разложение многочлена с действительными коэффициентами на линейные и квадратичные множители.

Опр. Многочлен 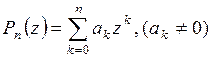(2) называется действительным, если a_k – действительные числа.

Лемма: для действительного многочлена P_n(z) имеет место равенство: (2).

Доказательство основано на равенствах:

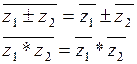
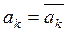(действительные числа)

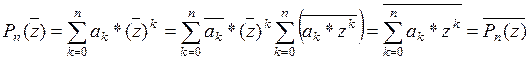
Теорема 1. Если 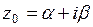- это комплексный корень кратности 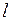действительного многочлена P_n(z), то 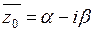тоже является корнем кратности b многочлена P_n(z), и тогда выполняется равенство: 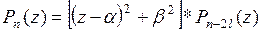(3), где 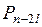- действительный многочлен степени n-2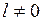при z=z₀ и z=. ().

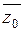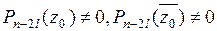Д-во:

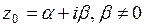, тогда в силу равенства (2): 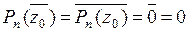, т.е. 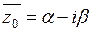тоже является корнем многочлена P_n(z), поэтому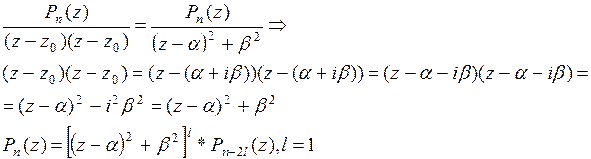

Если z₀ – корень P_n(z) кратности 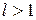, то можно показать, что 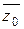- тоже корень P_n(z) той же кратности 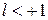. Повторяя процесс деления n раз, получим (3).

Замечание: многочлен 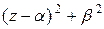можно преобразовать:

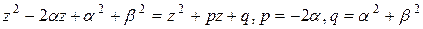. Получили действительный многочлен второй степени, у которого D<0, он имеет два комплексных сопряженных корня: z₁=.

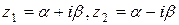Теорема 2. Многочлен P_n(z) со старшим коэффициентом A_n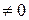может быть представлен в виде:

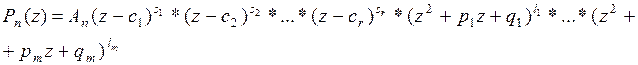
где c₁, c₂…c_r – действительные корни многочлена P_n(z) кратности s₁, s₂…s_r соответственно, а многочлены (z²+p_jz+q_j) – многочлены второй степени, имеющие комплексные сопряженные корни 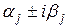, j=1,2…m, с кратностью 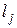, (s₁+s₂+…+s_r)+2(l₁+l₂+…l_m)=n.

Дата добавления: 2014-01-14