Пример. Проверить по определению, что А = 10/9 есть предел последовательности

Проверить по определению, что А = 10/9 есть предел последовательности

1 1.1 1.11 1.111 1.1111 …;

Пусть ε > 0 – некоторое малое число. Тогда для некоторого k можно записать 10^-k+1 > ε > 10^-k,

т.е. ε = 0.000…** (k -1 нулей после дес. точки).

Покажем, что для всех n ≥ k + 1 выполнено неравенство

|a_n - A| < ε.

Действительно, А = 10/9 = 1.1111… имеет ∞ число единиц после дес. точки, a_n имеет (n - 1) единиц после дес. точки. Значит, разность А - a_n имеет (n - 1) нулей после дес. точки, а дальше единицы. Так как n ≥ k + 1, то А - a_n имеет более, чем k нулей после дес. точки, значит, |a_n - A| < ε.

Определение 3. Последовательность называется сходящейся, если она имеет предел.

Докажем несколько предложений о пределах последовательности, вытекающих из определения.

Предложение 1. Если , то все элементы последовательности лежат в ε-окрестности точки А, за исключением конечного числа.

Доказать, опираясь на определение.

Предложение 2. Одна и та же последовательность не может иметь двух различных пределов.

Док-во. От противного. Пусть , , А ≠ В. Возьмём ε < половины длины отрезка, соединяющего А и В.

ε –окр. А ε –окр. В

А В

Согласно предложению 1, вне ε –окр. А имеется лишь конечное число элементов последовательности, а значит, в ε –окр. В имеется конечное число элементов последовательности, что противоречит предложению 1.

Предложение 3. Сходящаяся последовательность ограничена сверху и снизу.

Док-во. Если A – предел последовательности, то согласно предложению 1, все её члены лежат в какой-либо ε –окр. А, за исключением конечного множества М. Тогда все члены последовательности больше наименьшего из М, лежащего слева … (и т.д., пояснить, если требуется).

Замечание. Если последовательность сходится, то это не означает, что есть наибольший или наименьший член этой последовательности (см. рассмотренный пример 5). Однако, у сходящейся последовательности есть или наибольший или наименьший член. В рассмотренном примере 5 есть наименьший член = 1.

Определение 4. Если есть две последовательности {a_n} и {b_n}, то их суммой, разностью, произведением, частным наз. последовательности {a_n + b_n}, {a_n - b_n}, {a_n ∙ b_n}, {a_n / b_n} (частное определено только если b_n ≠ 0 для всех n).

Предложение 4. (без доказ-ва) Если существуют пределы последовательностей {a_n} и {b_n}, то

= ± ;

= ∙;

= (если≠ 0).

Определение 5. Последовательность {a_n} наз. фундаментальной, если 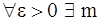такое, что 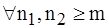выполнено неравенство .

Определение 6. Две фундаментальных последовательности {a_n} и {b_n} наз. эквивалентными, если

.

Определение 7. Множество фунд. послед-й, попарно эквив-х между собой, наз. классом эквивалентных фундаментальных последовательностей.

Определение 8. Действительными числами наз. классы эк-вивалентных фунд. последовательностей рациональных чисел.

Предложение 5. (без док-ва). Всякая фундаментальная пос-ледовательность действительных чисел имеет предел в множе-стве действительных чисел.

Замечание. Не всякая фунд. последовательность рац. чисел имеет предел в множестве рац. чисел.

Пример. 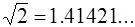. Рассмотрим последовательность

1 1.4 1.41 1.414 1.4142 1.41421 …

Эта последовательность имеет предел , который не являет-ся рациональным числом. Значит, эта последовательность не имеет предела в множестве рац. чисел, хотя является фунда-ментальной (проверить фундаментальность, если не очевидно аудитории).

Предложение 6 (без док-ва, пояснить очевидный интуитив-ный смысл).

а) Монотонно возрастающая и ограниченная сверху последовательность действительных чисел имеет предел.

б) Монотонно убывающая и ограниченная снизу последовательность действительных чисел имеет предел.

Дата добавления: 2014-01-14