Понятие определённого интеграла

Обе рассмотренные задачи привели нас к одной и той же математической операции над функциями различного происхождения, заданными на некоторых отрезках. Формулы (1) и (2) аналогичны друг другу в том смысле, что имеют одинаковую структуру и получены в результате выполнения однотипных действий.

Операция, приведшая к формулам (1) и (2) называется интегрированием функции на отрезке, а её результат число – называется определённым интегралом.

Пусть произвольная функция y=f (x) непрерывна на отрезке .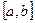

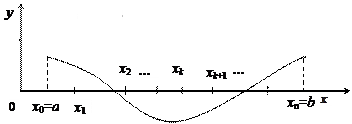Рис. 10.

Разобьём 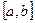на n (рис. 10) частей произвольным образом точками а = x ₀, x ₁, x ₂,… x_k, x_{k +1},… x_{n -1}, x_n = b.

Обозначим .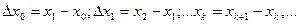

В каждом из элементарных промежутков выберем произвольную точку :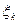

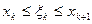(k =0,1,… n -1) и

вычислим значение функции f (x) в этих точках: 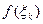(k =0,1,… n -1). Составим сумму:

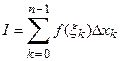(3)

Эта сумма называется интегральной суммой для функции f (x) при данном разбиении отрезка 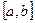на частичные и данном выборе промежуточных точек .

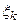Интегральных сумм для данной функции и данного отрезка можно составить бесконечно много, так как они

зависят от способа разбиения отрезка 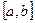и выбора точек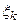. Пусть разбиение отрезков делается сколь угодно мелким, т.е. 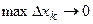. При этом очевидно число n элементарных отрезков в разбиении стремиться к бесконечности, и интегральная сумма будет каким-то образом изменяться.

Если существует предел интегральной суммы (3), когда разбиение отрезка 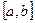делается сколь угодно мелким, и если этот предел не зависит ни от способа разбиения отрезка на частичные, ни от выбора промежуточных точек 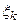, то этот предел называется определенным интегралом от функции f(x) на отрезке 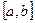и обозначается:

.

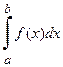Здесь а – нижний предел интегрирования, b – верхний предел интегрирования. Таким образом, по определению:

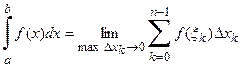. (4)

Из определения следует, что определённый интеграл – это число, зависящее от вида функции f (x) и от чисел a и b, но не зависящее от х ₀. Теперь в рассмотренных примерах можно записать:

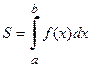
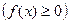(5)

и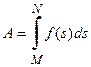

Из формулы (5) следует геометрический смысл определённого интеграла при 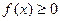: определённый интеграл от неотрицательной функции численно равен площади соответствующе криволинейной трапеции.

Из определения непосредственно вытекает, что

.

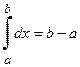Определение (4) интеграла сделано для случая a<b. Если a>b, то примем по определению:

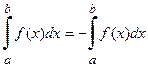, а если a=b, то .

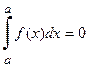Функция, для которой существует определённый интеграл на отрезке 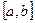, называется интегрируемой на этом отрезке.

Теорема: Функция f(x) непрерывная на отрезке 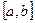, интегрируема на этом отрезке.

Эта теорема даёт достаточное условие интегрируемости. Среди разрывных функций может быть как интегрируемые, так и не интегрируемые функции.

В частности, можно доказать, что для всякой ограниченной на отрезке 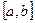функции, имеющей на нём конечное число точек разрыва, существует определённый интеграл.

Дата добавления: 2014-01-14