Общие постановки задач исследования функционирования проектируемых изделий или систем и методические подходы их решения

Рассмотрим задачу исследования функционирования изделия в общей постановке, безотносительно к виду его основного назначения.

Пусть имеется некоторый процесс или операция, которую выполняет наше проектируемое изделие или система, на исход которого мы можем в какой-то мере влиять, выбирая тем или другим способом зависящие от нас параметры (показатели качества) проектируемого изделия. Эффективность функционирования изделия или системы характеризуется каким-то численным показателем W, который мы бы хотели обратить в минимум. То есть критерием эффективности является минимум показателя W.

Предположим, что тем или иным способом математическая модель функционирования изделия или системы построена; она позволяет вычислить показатель эффективности W при любых выбранных параметрах (показателях качества) нашего изделия или системы, для любой совокупности условий, в которых оно (она) функционирует.

Рассмотрим сначала наиболее простой случай: все факторы, от которых зависит успех функционирования изделия, делятся на две группы:

— заданные, заранее известные факторы (условия функционирования) α={α₁,α₂,…}, на которые мы влиять не можем;

— зависящие от нас факторы (параметры изделия – показатели качества, элементы решения) Х={х₁, х₂...} которые мы, в известных пределах, можем выбирать по своему усмотрению.

Этот случай, в котором факторы, влияющие на исход функционирования изделия, либо заранее известны, либо зависят от нас, мы будем называть детерминированным.

Заметим, что под «заданными условиями» α={α₁,α₂,…}, могут пониматься не только обычные числа, но и функции, в частности ограничения, наложенные на элементы решения. Равным образом, элементы решения Х={х₁, х₂...} также могут быть не только числами, но и функциями.

Показатель эффективности W зависит от обеих групп факторов: как от заданных условий, так и от элементов решения. Запишем эту зависимость в виде общей символической формулы:

X^о =arg min W (α₁,α₂,…; х₁, х₂...).

X

Так как математическая модель построена, будем считать, что зависимость W (α₁,α₂,…; х₁, х₂...) нам известна, и для любых α={α₁,α₂,…}; X={х₁, х₂...} мы можем найти W.

Тогда задачу оптимизации параметров проектируемого изделия или системы можно математически сформулировать так:

При заданных условиях α={α₁,α₂,…}найти такие элементы решения Х={х₁, х₂...} (показатели качества изделия или системы), которые обращают показатель W в минимум.

Минимум показателя W является критерием оптимизации проектируемого изделия или системы.

Перед нами — типично математическая задача, относящаяся к классу так называемых вариационных задач. Методы решения таких задач подробно разработаны в математике. Простейшие из этих методов («задачи на максимум и минимум») хорошо известны каждому инженеру. Для нахождения максимума или минимума (короче, экстремума) функции нужно продифференцировать ее по аргументу (или аргументам, если их несколько), приравнять производные нулю и решить полученную систему уравнений.

Однако этот простой метод в задачах исследования операций имеет ограниченное применение. Причин этому несколько.

1. Когда аргументов X={х₁, х₂...} много (а это типично при проектировании систем), совместное решение системы уравнений полученных дифференцированием основной зависимости зачастую оказывается не проще а сложнее чем непосредственный поиск экстремума.

2. В случае, когда на элементы решения X={х₁, х₂...} наложены ограничения (т. е., область их изменения ограничена), часто экстремум наблюдается не в точке, где производные обращаются в нуль, а на границе области возможных решений. Возникает специфическая математическая задача «поиска экстремума при наличии ограничений», не укладывающаяся в схему классических вариационных методов.

3. Наконец, производных, о которых идет речь, может вовсе не существовать, например, если аргументы X={х₁, х₂...} изменяются не непрерывно, а дискретно, или же сама функция W имеет особенности.

Общих математических методов нахождения экстремумов функций любого вида при наличии произвольных ограничений не существует. Однако для случаев, когда функция и ограничения обладают определенными свойствами, современная математика предлагает ряд специальных методов. Например, если показатель эффективности W зависит от элементов решения X={х₁, х₂...} линейно и ограничения, наложенные на х₁, х₂... также имеют вид линейных равенств (или неравенств), максимум функции W находится с помощью специального аппарата, так называемого линейного программирования (например, используется симплекс метод). Если эти функции обладают другими свойствами (например, выпуклы или являются квадратичными), применяется аппарат «выпуклого», или «квадратичного» программирования более сложный по сравнению с линейным программированием, но все же позволяющий в приемлемые сроки найти решение. Если функционирование системы естественным образом расчленяется на ряд шагов» или «этапов» (например, хозяйственных лет), а показатель эффективности W выражается в виде суммы показателей достигнутых за отдельные этапы, то для нахождения решения, обеспечивающего максимальную эффективность, может быть применен метод динамического программирования (см. теорию исследования операций).

Если функционирование изделия (системы) описывается обыкновенными дифференциальными уравнениями, а управление, меняющееся со временем, представляет собой некоторую функцию x(t), то для нахождения оптимального управления может оказаться полезным специально разработанный метод Л. С. Понтрягина.

Таким образом, в рассматриваемом детерминированном случае задача отыскания оптимального решения сводится к математической задаче отыскания экстремума функции W; эта задача может быть весьма сложной (особенно при многих аргументах), но, в конце концов, является вычислительной задачей, которую, особенно при наличии быстродействующих ЭВМ, удается так или иначе решить до конца. Трудности, возникающие при этом, являются расчетными, а не принципиальными.

Мы рассмотрели самый простой, полностью детерминированный случай, когда все условия функционирования изделия α₁,α₂,…известны, и любой выбор решения Х={х₁, х₂...} приводит к вполне определенному значению показателя эффективности W.

К сожалению, этот простейший случай не так уж часто встречается на практике. Гораздо более типичен случай, когда не все условия функционирования известны заранее, а некоторые из них содержат элемент неопределенности. Например, успех операции может зависеть от метеорологических условий, которые заранее неизвестны, или от колебаний спроса и предложения, заранее трудно предвидимых, связанных с капризами моды, или же от поведения разумного противника, действия которого заранее неизвестны.

В подобных случаях эффективность применения изделия зависит уже не от двух, а от трех категорий факторов:

— условия выполнения операции α={α₁,α₂,…}, которые известны заранее и изменены быть не могут;

— неизвестные условия или факторы Y={Y₁, Y₂,...};

— элементы решения Х={х₁, х₂...}, которые нам предстоит выбрать.

Пусть эффективность изделия или системы характеризуется некоторым показателем W, зависящим от всех трех групп факторов. Это мы запишем в виде общей формулы:

W = W (α₁,α₂,…; Y1, Y2,...; х₁, х₂...).

Если бы условия α={α₁,α₂,…} были известны, мы могли бы заранее подсчитать критерий и выбрать такое решение Х={х₁, х₂...}, при котором показатель W минимизируется.

X^o = arg min W (α₁,α₂,…; Y1, Y2,...; х₁, х₂...).

X

Беда в том, что параметры Y={Y₁, Y₂,...} нам неизвестны, а значит, неизвестен и зависящий от них показатель эффективности W при любом решении. Тем не менее, задача выбора решения по-прежнему стоит перед нами. Ее можно сформулировать так:

При заданных условиях α={α₁,α₂,…} с учетом неизвестных факторов Y={Y₁, Y₂,...} найти такие элементы решения Х^o={х₁, х₂...}, которые по возможности обращали бы в минимум показатель эффективности W.

Это — уже другая, не чисто математическая задача (недаром в ее формулировке сделана оговорка «по возможности»). Наличие неизвестных факторов Y={Y₁, Y₂,...} переводит нашу задачу в другую категорию: она превращается в задачу о выборе решения в условиях неопределенности.

Давайте будем честны: неопределенность есть неопределенность. Если условия функционирования изделия неизвестны, мы не имеем возможности так же успешно организовать математическую модель с учетом этих неопределенностей, как мы это сделали бы, если бы располагали большей информацией. Поэтому любое решение, принятое в условиях неопределенности, хуже решения, принятого во вполне определенной ситуации. Наше дело — сообщить своему решению в наибольшей возможной мере черты разумности. Решение, принятое в условиях неопределенности, но на основе математических расчетов, будет все же лучше решения, выбранного наобум.

Задачи о выборе решения в условиях неопределенности встречаются нам в жизни на каждом шагу. Пусть, например, мы собрались ехать в отпуск, взяв с собой чемодан ограниченного объема, причем вес чемодана не должен превышать того, при котором мы можем носить его без посторонней помощи (условия α={α₁,α₂,…}). Погода в районах путешествия заранее неизвестна (условия Y={Y₁, Y₂,...}). Спрашивается, какие предметы одежды (Х={х₁, х₂...}) следует взять с собой?

Эту задачу мы, разумеется, решаем без всякого математического аппарата, хотя, по-видимому, не без опоры на какие-то численные данные (хотя бы на вероятности прогноза морозной или дождливой погоды в районах путешествия в данное время года). Однако, если нужно принять более серьезное и ответственное решение (например, о характеристиках проектируемой плотины в районе возможных паводков, или о выборе типа посадочного устройства для посадки на планету с неизвестными свойствами поверхности, или о выборе образца вооружения для борьбы с противником, характеристики которого заранее неизвестны), то выбор решения в обязательном порядке должен быть подкреплен математическими расчетами, облегчающих этот выбор и придающие этому выбору, в доступной мере, черты разумности.

Применяемые при этом методы существенно зависят от того, какова природа неизвестных факторов Y={Y₁, Y₂,...} и какими ориентировочными сведениями о них мы располагаем.

Наиболее простым и благоприятным для расчетов является случай, когда неизвестные факторы Y={Y₁, Y₂,...} представляют собой случайные величины (или же случайные функции), о которых имеются статистические данные, характеризующие их распределение.

Пусть, например, мы проектируем железнодорожную сортировочную станцию, стремясь оптимизировать процесс обслуживания прибывающих на эту станцию грузовых поездов. Заранее неизвестны ни точные моменты прибытия поездов, ни количество вагонов в каждом поезде, ни адреса, по которым направляются вагоны. Все эти характеристики представляют собой случайные величины, закон распределения каждой из которых (и их совокупности) может быть определен по имеющимся данным обычными методами математической статистики.

Аналогично, в каждой военной операции присутствуют случайные факторы, связанные с рассеиванием снарядов, со случайностью моментов обнаружения целей и т. п. В принципе все эти факторы могут быть изучены методами теории вероятностей, и для них могут быть получены законы распределения (или, по крайней мере, числовые характеристики).

В случае, когда неизвестные факторы, фигурирующие в операции — Y={Y₁, Y₂,...} — являются обычными случайными величинами (или случайными функциями), распределение которых, хотя бы ориентировочно, известно, для оптимизации решения может быть применен один из двух приемов:

— искусственное сведение к детерминированной схеме;

— «оптимизация в среднем».

Остановимся более подробно на каждом из этих приемов.

Первый прием сводится к тому, что неопределенная, вероятностная картина явления приближенно заменяется детерминированной. Для этого все участвующие в задаче случайные факторы Y={Y₁, Y₂,...} приближенно заменяются не случайными (как правило, их математическими ожиданиями). Этот прием применяется по преимуществу в грубых, ориентировочных расчетах, когда диапазон случайных изменений величин Y={Y₁, Y₂,...}сравнительно мал, т. е. они без большой натяжки могут рассматриваться как не случайные. Заметим, что тот же прием замены случайных величин их математическими ожиданиями может успешно применяться и в случаях, когда величины Y={Y₁, Y₂,...}обладают большим разбросом, но показатель эффективности W зависит от них линейно (или почти линейно).

Второй прием («оптимизация в среднем»), более сложный, применяется, когда случайность величин Y={Y₁, Y₂,...} весьма существенна и замена каждой из них ее математическим ожиданием может привести к большим ошибкам.

Рассмотрим этот случай более подробно. Пусть показатель эффективности W существенно зависит от случайных факторов (будем для простоты считать их случайными величинами) Y={Y₁, Y₂,...}; допустим, что нам известно распределение этих факторов, скажем, плотность распределения f(у₁, у₂...). Предположим, что проектируемая система или изделие применяется много раз, причем условия Y₁, Y₂..меняются от раза к разу случайным образом. Какое решение Х={х₁, х₂...} следует выбрать? Очевидно, то, при котором операция в среднем будет наиболее эффективна, т. е. математическое ожидание критерия эффективности W будет минимально. Таким образом, нужно выбирать такое решение Х={х₁, х₂...}, при котором обращается в минимум математическое ожидание показателя эффективности М[W]:

.

Такую оптимизацию мы будем называть «оптимизацией в среднем».

А как же с элементом неопределенности? Конечно, в какой-то мере он сохраняется. Успешность каждой отдельной операции, осуществляемой при случайных, заранее неизвестных значениях Y={Y₁, Y₂,...} может сильно отличаться от ожидаемой средней величины, как в большую, так, к сожалению, и в меньшую сторону. При многократном использовании изделия или системы эти различия, в среднем, сглаживаются; однако, нередко данный способ оптимизации решения, за неимением лучшего, применяется и тогда, когда изделие уникальное и применяется всего один всего несколько раз или даже один раз. Тогда надо считаться с возможностью неприятных неожиданностей в каждом отдельном случае. Утешением нам может служить мысль о том, что «оптимизация в среднем» все же лучше, чем выбор решения без всяких обоснований. Применяя этот прием к многочисленным (хотя бы и различным) операциям, все же мы в среднем выигрываем больше, чем, если бы совсем не пользовались расчетом.

Для того, чтобы составить себе представление о том, чем мы рискуем в каждом отдельном случае, желательно, кроме математического ожидания показателя эффективности, оценивать также и его дисперсию (или средне квадратичное отклонение).

Наиболее трудным для исследования является тот случай неопределенности, когда неизвестные факторы Y={Y₁, Y₂,...} не могут быть изучены и описаны с помощью статистических методов: их законы распределения или не могут быть получены (соответствующие статистические данные отсутствуют), или, что еще хуже, таких законов распределения вовсе не существует. Это бывает, когда явление, о котором идет речь, не обладает свойством статистической устойчивости. Например, мы знаем, что на Марсе возможно наличие органической жизни, и некоторые ученые даже считают его весьма вероятным, но совершенно невозможно подсчитать эту вероятность на основе каких-либо статистических данных. Другой пример: предположим, что эффективность проектируемого вооружения сильно зависит от того, будет ли предполагаемый противник к моменту начала боевых действий располагать средствами защиты, и если да, то какими именно? Очевидно, нет никакой возможности подсчитать вероятности этих гипотез — самое большее, их можно назначить произвольно, что сильно повредит объективности исследования.

В подобных случаях, вместо произвольного и субъективного назначения вероятностей с дальнейшей «оптимизацией в среднем», рекомендуется рассмотреть весь диапазон возможных условий Y={Y₁, Y₂,...} и составить представление отом, какова эффективность применения проектируемого изделия во всем этом диапазоне и как на нее влияют неизвестные условия. При этом задача исследования приобретает новые методологические особенности.

Действительно, рассмотрим случай, когда эффективность применения изделия W зависит, помимо заданных условий α={α_1, α₂...}и элементов решения X={х₁, х₂...} еще и от ряда неизвестных факторов Y={Y₁, Y₂,...}нестатистической природы, о которых никаких определенных сведений нет, а можно делать только предположения. Попробуем все же решить задачу. Зафиксируем мысленно параметры Y={Y₁, Y₂,...}., придадим им вполне определенные значения Y₁=y₁, Y₂ = y₂..., и переведем тем самым в категорию заданных условий α={α_1, α₂...}.Для этих условий мы в принципе можем решить задачу исследования функционирования изделия или системы и найти соответствующее оптимальное решение X={х₁, х₂...}. Его элементы, кроме заданных условий α={α_1, α₂…}, очевидно, будут зависеть еще и от того, какие частные значения мы придали условиям Y={Y₁, Y₂,...}

х₁ = х ₁ ( α_1, α₂...; y₁, y₂....);

х₂ = х ₂ ( α_1, α₂...; y₁, y₂....).

Такое решение, оптимальное для данной совокупности условий y₁, y₂.... (и только для нее), называется локально-оптимальным. Это решение, как правило, уже не оптимально для других значений Y₁, Y₂.... Совокупность локально-оптимальных решений для всего диапазона условий Y={Y₁, Y₂,...}, дает нам представление о том, как мы должны были бы поступать, если бы неизвестные условия Y={Y₁, Y₂,...} были нам в точности известны. Поэтому локально-оптимальное решение, на получение которого зачастую тратится много усилий, имеет в случае неопределенности сугубо ограниченную ценность. Совершенно очевидно, что в данном случае следует предпочесть не решение, строго оптимальное для каких-то определенных условий, а компромиссное решение, которое, не будучи, может быть, строго оптимальным ни для каких условий, оказывается приемлемым в целом диапазоне условий. Такое решение в отличии от оптимального еще называют рациональным.

В настоящее время полноценной математической «теории компромисса» еще не существует, хотя в теории решений и имеются некоторые попытки в этом направлении. Обычно окончательный выбор компромиссного решения осуществляется человеком (лицом, принимающим решение – ЛПР), который, опираясь на расчеты, может оценить и сопоставить сильные и слабые стороны каждого варианта решения в разных условиях и на основе этого сделать окончательный выбор. При этом необязательно (хотя иногда и любопытно) знать точный локальный оптимум для каждой совокупности условий y₁, y₂.... Таким образом, классические вариационные и новейшие оптимизационные методы математики отступают в данном случае на задний план.

В последнюю очередь рассмотрим своеобразный случай, возникающий в так называемых конфликтных ситуациях, когда неизвестные параметры Y={Y₁, Y₂,...} зависят не от объективных обстоятельств, а от активно противодействующего нам противника. Такие ситуации характерны для боевых действий, отчасти для спортивных соревнований, в конкуренции и т. д.

При выборе решений в подобных случаях может оказаться полезным математический аппарат так называемой теории игр - математической теории конфликтных ситуаций. Модели конфликтных ситуаций, изучаемые в теории игр, основаны на предположении, что мы имеем дело с разумным и дальновидным противником, всегда выбирающим свое поведение наихудшим для нас (и наилучшим для себя) способом. Такая идеализация конфликтной ситуации в некоторых случаях может подсказать нам наименее рискованное, «перестраховочное» решение, которое необязательно принимать, но, во всяком случае, полезно иметь в виду.

Постановка таких игровых задач заключается в том, что цель проектируемой системы является, например, максимизировать выбранный критерий эффективности, а задача противника минимизировать этот критерий. Тогда формализованная постановка задачи может быть записана следующим образом:

.

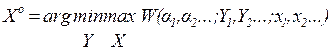Наконец, сделаем одно общее замечание. При обосновании решения в условиях неопределенности, что бы мы ни делали, элемент неопределенности остается. Поэтому неразумно предъявлять к точности таких решений слишком высокие требования. Вместо того, чтобы после скрупулезных расчетов однозначно указать одно единственное, в точности оптимальное (в каком-то смысле) решение, всегда лучше выделить область приемлемых решений, которые оказываются несущественно хуже других, какой бы точкой зрения мы ни пользовались. В пределах этой области могут произвести свой окончательный выбор ответственные за него лица.

Многокритериальные оптимизационные задачи.

Выше мы рассмотрели задачу исследования функционирования проектируемого изделия, где требовалось так выбрать решение, чтобы максимизировать (или минимизировать) один-единственный показатель эффективности W. На практике часто встречается случай, когда проектируемое изделие или система выполняет несколько функций, или говорят, что оно имеет несколько целей. В этих случаях эффективность приходится оценивать не по одному, а сразу по нескольким критериям. Одни качественные показатели изделия желательно сделать больше, другие — меньше.

Как правило, эффективность больших по объему процессов функционирования больших сложных технических систем и сложных выполняемых ими операций не может быть исчерпывающим образом охарактеризована с помощью одного показателя; на помощь ему приходится привлекать и другие, дополнительные.

Например, при оценке деятельности промышленного предприятия приходится учитывать целый ряд показателей, как то:

— прибыль,

— полный объем продукции («вал»),

— себестоимость и т. д.

При анализе боевой операции, в которой участвует проектируемое изделие помимо основного показателя, характеризующего ее эффективность (например, математическое ожидание причиненного противнику ущерба), приходится учитывать и ряд дополнительных критериев, как то:

— собственные потери,

— время выполнения операции,

— расход боеприпасов и т. д.

Такая множественность показателей эффективности, из которых некоторые желательно максимизировать, а другие — минимизировать, характерна для любой сколько-нибудь сложной задачи исследования операций. Возникает вопрос: как же быть?

Прежде всего надо подчеркнуть, что выдвинутые требования, вообще говоря, несовместимы. Решение, обращающее в максимум один какой-то показатель W₁, как правило, не обращает ни в максимум, ни в минимум другие показатели W₂, W₃,.... Поэтому широко распространенная формулировка «достижение максимального эффекта при минимальных затратах» для научного исследования не подходит. Корректной является любая из формулировок «достижение максимального эффекта при заданных затратах» или же «достижение заданного эффекта при минимальных затратах».

В общем случае не существует решения, которое обращало бы в максимум один показатель W₁ и одновременно в максимум (или минимум) другой показатель W₂, тем более, такого решения не существует для нескольких показателей. Однако количественными анализ эффективности может оказаться весьма полезным и в случае нескольких показателей эффективности.

Прежде всего, он позволяет заранее отбросить явно нерациональные варианты решений, уступающие лучшим вариантам по всем показателям.

Проиллюстрируем сказанное на примере. Пусть анализируется боевая операция б, оцениваемая по двум показателям:

W — вероятность выполнения боевой задачи («эффективность»);

S — стоимость израсходованных средств.

Очевидно, первый показатель желательно обратить в максимум, а второй — в минимум. Предположим для простоты, что предлагается на выбор конечное число — 20 различных вариантов решения; обозначим их Х₁, X₂,..., Х_n. Для каждого из них известны значения обоих показателей W и S.

Изобразим для наглядности каждый вариант решения в виде точки на плоскости с координатами W и S (рис. 1.1).

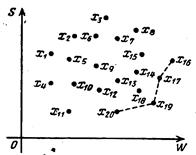
Рис. 1.1

Рассматривая рисунок, мы видим, что некоторые варианты решения «неконкурентоспособны» и заранее должны быть отброшены. Действительно, те варианты, которые имеют над другими вариантами с той же стоимостью S преимущество по эффективности W, должны лежать на правой границе области возможных вариантов. Те же варианты, которые при равной эффективности обладают меньшей стоимостью, должны лежать на нижней границе области возможных вариантов.

Какие же варианты следует предпочесть при оценке эффективности по двум показателям? Очевидно, те, которые лежат одновременно и на правой, и на нижней границе области (см. пунктирную линию на рис. 1.1). Действительно, для каждого из вариантов, не лежащих на этом участке границы, всегда найдется другой вариант, не уступающий ему по эффективности, но зато более дешевый или, наоборот, не уступающий ему по дешевизне, но зато более эффективный. Таким образом, из 20 предварительно выдвинутых вариантов большинство выпадает из соревнования, и нам остается только проанализировать оставшиеся четыре варианта: Х₁₆, Х₁₇, Х₁₈, Х₂₀. Из них Х₁₆ — наиболее эффективный, но зато сравнительно дорогой; Х₂₀ — самый дешевый, но зато не столь эффективный. Дело принимающего решение — разобраться в том, какой ценой мы согласны оплатить известное повышение эффективности или, наоборот, какой долей эффективности мы согласны пожертвовать, чтобы не нести слишком больших материальных потерь.

Аналогичный предварительный просмотр вариантов (хотя и без такой наглядной геометрической интерпретации) может быть произведен и в случае многих показателей: W₁, W₂, W₃, W_k.

Такая процедура предварительной отбраковки неконкурентоспособных вариантов решения должна всегда предшествовать решению задачи исследования операций с несколькими показателями. Это, хотя и не снимает необходимости компромисса, но существенно уменьшает множество решений, в пределах которого осуществляется выбор.

Ввиду того, что комплексная оценка сразу по нескольким показателям затруднительна и требует размышлений, на практике часто пытаются искусственно объединить несколько показателей в один обобщенный критерий. Нередко в качестве такого обобщенного (составного) критерия берут дробь; в числителе ставят те показатели W₁, …, W_m, которые желательно увеличить, а в знаменателе, — те, которые желательна уменьшить:

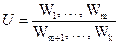
Например, если речь идет о боевой операции, в числителе ставят такие величины, как «вероятность выполнения боевой задачи» или «потери противника»; в знаменателе — «собственные потери», «расход боеприпасов», «время выполнения операции» и т. п.

Общим недостатком «составных критериев» такого типа является, то, что недостаток эффективности по одному показателю всегда можно скомпенсировать за счет другого (например, малую вероятность выполнения боевой задачи — за счет малого расхода боеприпасов, и т. п.). Критерии подобного рода напоминают в шутку предложенный Львом Толстым «критерий оценки человека» в виде дроби, где числитель — истинные достоинства человека, а знаменатель — его мнение о себе. Несостоятельность такого критерия очевидна: если принять его всерьез, то человек, почти без достоинств, но зато совсем без самомнения, будет иметь бесконечно большую ценность!

Часто «составные критерии» предлагаются не в виде дроби, а в виде «взвешенной суммы» отдельных показателей эффективности:

,

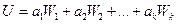где а₁, а₂,...,a_k, — положительные или отрицательные коэффициенты. Положительные ставятся при тех показателях, которые желательно максимизировать; отрицательные — при тех, которые желательно минимизировать. Абсолютные значения коэффициентов («веса») соответствуют степени важности показателей.

Нетрудно убедиться, что составной критерий этого вида по существу ничем не отличается от предыдущего критерия и обладает теми же недостатками (возможность взаимной компенсации разнородных показателей). Поэтому некритическое пользование любого вида «составными» критериями чревато опасностями и может привести к неправильным рекомендациям. Однако, в некоторых случаях, когда «веса» не выбираются произвольно, а подбираются так, чтобы составной критерий наилучшим образом выполнял свою функцию, удается получить с его помощью некоторые результаты ограниченной ценности.

В некоторых случаях задачу с несколькими показателями удается свести к задаче с одним-единственным показателем, если выделить только один (главный) показатель эффективности W₁ и стремиться его обратить в максимум, а на остальные, вспомогательные показатели W₂, W₃... наложить только некоторые ограничения вида:

W₂≥ω₂, W₃≤ω₃, W_m≥ω_m, W_m+1≤ω_m+1, …, W_k≤ω_k.

Эти ограничения, разумеется, войдут в комплекс заданных условий α={α₁, α₂, }.

Например, при оптимизации параметров бомбардировщика оценка его применения в бомбардировочном налете можно потребовать, чтобы нанесенный противнику ущерб был максимален, но при этом собственные потери и стоимость всей операции не выходили за известные пределы.

При такой постановке задачи все показатели эффективности, кроме одного, главного, переводятся в разряд заданных условий операции. Варианты решения, не укладывающиеся в заданные границы, сразу же отбрасываются, как неконкурентоспособные. Полученные рекомендации, очевидно, будут зависеть от того, как выбраны ограничения для вспомогательных показателей. Чтобы определить насколько это влияет на окончательные рекомендации по выбору решения, полезно проварьировать ограничения в разумных пределах.

Наконец, возможен еще один путь построения компромиссного решения, который можно назвать «методом последовательных уступок». Предположим, что показатели эффективности расположены в порядке убывающей важности: сначала основной W₁ затем другие, вспомогательные: W₂, W₃,... Для простоты будем считать, что каждый из них нужно обратить в максимум (если это не так, достаточно изменить знак показателя). Процедура построения компромиссного решения сводится к следующему. Сначала ищется решение, обращающее в максимум главный показатель эффективности W₁. Затем назначается, исходя из практических соображений и точности, с какой известны исходные данные (а часто она бывает небольшой), некоторая «уступка» ΔW₁ которую мы согласны допустить для того, чтобы обратить в максимум второй показатель W₂. Налагаем на показатель W, ограничение, чтобы он был не меньше, чем W₁*-ΔW₁, где W₁* —. максимально возможное значение W₁ и при этом ограничении ищем решение, обращающее в максимум W₂. Далее снова назначается «уступка» в показателе W₂, ценой которой можно максимизировать W₃ и т. д.

Такой способ построения компромиссного решения хорош тем, что здесь сразу видно, ценой какой «уступки» в одном показателе приобретается выигрыш в другом.

Заметим, что свобода выбора решения, приобретаемая ценой даже незначительных «уступок», может оказаться существенной, так как в районе максимума обычно эффективность решения меняется очень слабо

Так или иначе, при любом способе формализации, задача количественного обоснования решения по нескольким показателям остается не до конца определенной, и окончательный выбор решения определяется волевым актом ЛПР. Дело исследователя — предоставить в распоряжение ЛПР достаточное количество данных, позволяющих ему всесторонне оценить преимущества и недостатки каждого варианта решения и, опираясь на них, сделать окончательный выбор.

Пример 8. Целью проектирования является выбор площадей поперечных сечений отдельных стержней b₁, b₂ и b₃ (оптимизируемые переменные проектирования) фермы (Рис. 1.2, где z₁ и z₂ - горизонтальное и вертикальное смещения общего узла) так, чтобы ферма была бы по возможности легкой и удовлетворялись ограничения на напряжение, устойчивость при продольном изгибе, смещение, и размеры стержней.

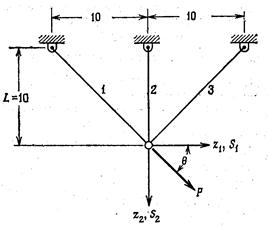
Рис. 1.2. Трехстержневая ферма.

Таким образом, исходя из поставленной задачи целевая функция W, представляет собой вес конструкции

W=ρg(10·2^1/2· b₁+10·b₂+10·2^1/2· b₃)

где ρg — удельный вес материала, из которого изготовлена ферма.

Чтобы этот функционал стал критерием определяют правило по которому выбирают оптимизируемые переменные Х ={b₁, b₂, b₃} (X – вектор оптимизируемых переменных). Критерий этой задачи записывается следующим образом.

X ^o=аrg min W(X),

X

или

X ^o = аrg min [ρg(10·2^1/2· b₁+10·b₂+10·2^1/2· b₃)].

X

Для окончательной постановки этой задачи добавляются еще функции ограничений определяющих ограничения на напряжение, устойчивость при продольном изгибе, смещение, и размеры стержней.

Решение подобной задачи возможно одним из градиентных методов.

Пример 9. Определить количественный состав трех типов маскировочных приборов (i=3), размещаемых на космическом корабле (КК), если вероятность маскировки на каждом из трех участков полета (j=3) КК определяется по формуле

Рj=1-1/(1+Σк_ij x_ij),

где к_ij – вероятности маскировки i-го средства на j-ом участке полета КК

и задано ограничение по суммарной массе этих приборов G_ПР.

Критерий (целевая функция) этой задачи имеет следующий вид:

X ^o = аrg mах П[1-1/(1+Σк_ij x_ij)].

X j i

При функции ограничений

ΣG_i x_i <=G_ПР.

Причем X={x₁, x₂, x₃}.

Решение этой последней задачи возможно методом направленного перебора.

Дата добавления: 2014-01-14