Скорость точки 2 страница

При естественном способе задания движения точки векторы скорости и ускорения 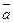определяют по их проекциям не на оси неподвижной системы отсчета Oxyz (как это было показано выше. для координатного способа задания движения), а на подвижные оси Мτnb, имеющие начало в точке М и движущиеся вместе с нею (рис.8). Эти оси называются естественными осями координат и вводятся следующим образом. Первой естественной осью является касательная

Мτ. Ее положительное направление совпадает с направлением единичного вектора касательной , направленного в сторону возрастания криволинейной координаты s.

Перпендикулярно касательной Мτ располагается нормальная плоскость. Нормаль, расположенная в соприкасающейся плоскости, называется главной нормалью Мn. Она является линией пересечения нормальной плоскости с соприкасающейся плоскостью. По главной нормали внутрь

вогнутости кривой направим единичный вектор . Он определяет положительное направление второй естественной оси. Плоскость, проведенная через точку М перпендикулярно главной нормали, называется спрямляющей плоскостью. На рис.8 соприкасающаяся, нормальная и спрямляющая плоскости обозначены соответственно цифрами I, II и III.

Нормаль, перпендикулярная главной нормали, называется бинормалью. Она является линией пересечения спрямляющей и нормальной плоскостей. Единичный вектор 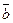, направленный по бинормали так, чтобы три вектора , и 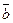образовывали правую систему осей координат, определит положительное направление третьей естественной оси.

Три взаимно перпендикулярные оси Мτ, Мn и Мb, положительное направление которых совпадает с направлениями единичных векторов , , , 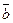называются естественными осями координат. Эти оси образуют в точке М естественный трехгранник. При движении точки М по кривой естественный трехгранник движется вместе с ней как твердое тело, поворачиваясь вокруг вершины, совпадающей с этой точкой М.

Рассмотрим теперь, как определяется ускорение при естественном способе задания движения точки.

Теорема. Ускорение точки равно векторной (геометрической) сумме касательного (тангенциального) и нормального ускорений.

ускорение точки лежит в соприкасающейся плоскости и раскладывается на две взаимно-перпендикулярные составляющие, одна из которых, (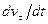) , направлена по касательной к траектории точки, а вторая, (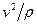) – по главной нормали к этой траектории. Первая составляющая называется касательным или тангенциальным ускорением, а вторая – нормальным ускорением точки. Составляющая же ускорения по прямой, перпендикулярной соприкасающейся плоскости, т. е. по бинормали к траектории точки, очевидно, равна нулю (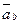 = 0).

Касательное ускорение обозначается через :

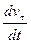
= = . (1.26)

Нормальное ускорение обозначается через :

= . (1.27)

Итак, ускорение точки при естественном способе задания движения определяется как сумма его касательной и нормальной составляющих:

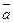= + , Модуль вектора ускорения равен

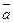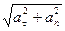│ │ = = , (1.29)

а его направление составляет с направлением главной нормали угол γ, тангенс которого равен

tg γ = 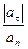( 1.30)

1.4. СВОЙСТВА КАСАТЕЛЬНОГО И НОРМАЛЬНОГО УСКОРЕНИЙ

Касательное ускорение точки.

Касательное ускорение характеризует изменение модуля вектора скорости.

1. Вектор касательного ускорения

= = .

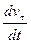
Производная 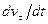= 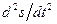представляет собой проекцию вектора касательного ускорения точки на касательную к ее траектории и называется алгебраическим касательным ускорением.

Условимся алгебраическое касательное ускорение обозначать ,т. е.

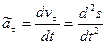. (1.31)

Очевидно, что

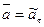
. (1.32)

Из этой формулы видно, что если алгебраическое касательное ускорение , то направления вектора касательного ускорения точки

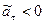и орта совпадают, если, , то направления векторов и противоположны. Следовательно, вектор касательного ускорения точки направлен по касательной к ее траектории в сторону роста криволинейной координаты если алгебраическое касательное ускорение >0, и в сторону убывания криволинейной координаты, если <0.

2. Случаи обращения в нуль касательного ускорения получаются из условия, что .

– Касательное ускорение точки равно нулю все время, пока v =| v_τ | = const. Если при движении точки величина ее скорости постоянная, то такое движение точки называется равномерным. В противном случае, т. е. когда v =| v_τ | ≠ const, движение точки называется неравномерным.

– Касательное ускорение обращается в нуль в те моменты времени, в которые алгебраическая скорость v_τ достигает экстремума, например максимума или минимума. При колебаниях маятника (рис.10) эти моменты соответствуют его прохождению через точку А.

Нормальное ускорение точки.

Нормальное ускорение точки существует лишь при криволинейном движении точки и характеризует изменение вектора скорости по направлению.

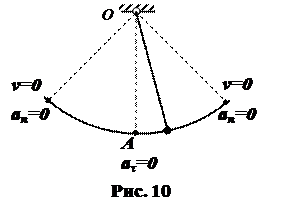1. Вектор нормального ускорения

.

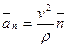Отсюда следует, что 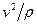– это проекция вектора нормального ускорения на главную нормаль. Она всегда положительна. Будем обозначать ее 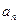, т. е.

. (1.33)

Поэтому, вектор нормального ускорения всегда направлен по главной нормали внутрь вогнутости траектории и по величине равен квадрату модуля скорости точки, деленному на радиус кривизны траектории в соответствующей точке.

2. Случаи обращения в нуль нормального ускорения получаются из условия

.

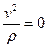– Нормальное ускорение равно нулю при прямолинейном движении точки: кривизна прямой линии k = 0, радиус кривизны ρ = ∞.

– Нормальное ускорение обращается в нуль в моменты времени, в которые скорость v = 0, т. е. в моменты изменения направления движения точки на противоположное. Для маятника (рис.10) такими моментами являются моменты отклонения маятника на наибольший угол как в одну сторону, так и в другую. Эти моменты соответствую мгновенным остановкам маятника.

– Нормальное ускорение обращается в нуль в точках перегиба траектории, где ρ = ∞ (рис.11). В этих точках происходит изменение выпуклости траектории на вогнутость, и наоборот.

1.5 ОПРЕДЕЛЕНИЕ ХАРАКТЕРА ДВИЖЕНИЯ ТОЧКИ

(об ускоренном, замедленном и равномерном движениях точки).

Как было определено (п.1.4), при неравномерном движении точки по траектории любой формы величина вектора скорости изменяется с течением времени (v =| v_τ | ≠ const).

Движение точки называется ускоренным или замедленным в течение некоторого промежутка времени, если в течение этого промежутка времени величина вектора скорости соответственно возрастает или убывает.

Теорема. Если знаки алгебраической скорости v_τ и алгебраического касательного ускорения точки одинаковые (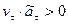), т. е. направления векторов скорости и ускорения совпадают, то точка движется ускор Если v_τ и имеют одинаковые знаки (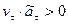), то производная >0, и, как известно из курса высшей математики, функция возрастающая. Тогда возрастает величина вектора скорости v, движение точки ускоренное и направления векторов и совпадают. Если v_τ и имеют разные знаки (), то функция убывающая, величина вектора скорости v убывает, движение точки замедленное, направления векторов и противоположны.

Следствие. Если угол между вектором скорости и вектором полного ускорения острый, то движение точки ускоренное, если тупой, то движение точки замедленное, если прямой, то движение точки равномерное.

енно; если знаки v_τ и различные (), т. е. направления векторов и противоположные, то точка движется замедленно.

Доказательство следствия опирается на рис.12.

Если угол между векторами и 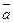острый (рис.12,а), то направления векторов и совпадают, и на основании теоремы движение точки ускоренное. Если угол тупой (рис.12,б), направления векторов и противоположные, движение точки замедленное. Случай, когда угол прямой(рис.12,в), требует оговорки. 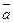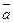Если вектор постоянно перпендикулярен вектору , то касательное ускорение =0, величина скорости постоянная и движение точки равномерное, если же векторы и перпендикулярны только в какое-то мгновение, то движение точки не является равномерным и равенство =0 означает, что в это мгновение величина скорости достигла экстремального значения (см. свойства касательного ускорения п.1.4).

1.6 ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ

Пользуясь полученными результатами, рассмотрим некоторые частные случаи движения точки. Они определяются значениями ее нормального и касательного ускорений.

1. ; =0. Если в течение некоторого промежутка времени нормальное и касательное ускорения точки равны нулю, то точка движется прямолинейно равномерно и ее полное ускорение 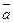=0. Заметим, что единственным движением, при котором полное ускорение точки постоянно равно нулю, является прямолинейное равномерное движение.

2. ; ≠ 0. Если в течение некоторого промежутка времени равно нулю нормальное ускорение точки и не равно нулю касательное ускорение, то не изменяется направление скорости, а изменяется ее величина, и точка движется прямолинейно неравномерно. Ее полное ускорение в этом случае = .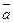

3. ; = 0. Если в течение некоторого промежутка времени не равно нулю нормальное ускорение точки и равно нулю касательное ускорение, то не изменяется величина скорости, а изменяется ее направление, и точка совершаетравномерное криволинейное движение. Ее полное ускорение в этом случае 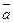= . При равномерном движении точки по траектории любой формы величина скорости является постоянной, следовательно, постоянна и алгебраическая скорость, т. е. 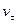= const. Найдем закон равномерного движения точки. Пусть в начальный момент времени (t= 0) криволинейная координата точки .Так как

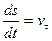, то .

Проинтегрируем это равенство в соответствующих пределах

. или .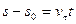

Окончательно находим закон равномерного криволинейного движения точки в виде

(1.35)

4. ; ≠ 0. Если в течение некоторого промежутка времени и нормальное и касательное ускорения точки отличны от нуля, то изменяетсякак направление, так и величина скорости, и точка совершает неравномерноекриволинейное движение. Ее полное ускорение в этом случае = +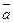

Равнопеременным движением называется такое движение по траектории любой формы, при котором величина касательного ускорения является постоянной, следовательно, постоянно и алгебраическое касательное ускорение, т. е. =const. Движение точки является равноускоренным, если алгебраическая скорость 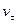и алгебраическоекасательное ускорение имеют одинаковые знаки. Есл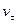и и имеют разные знаки, то движение точки является равнозамедленным. 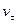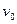Найдем закон равнопеременного движения, считая, что при t =0 , а = , где 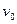—начальная скорость точки. Согласно (1.31) имеем:

, , ;

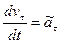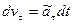следовательно,

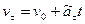. (1.36)

Так как , то с учетом (1.35)

,

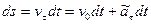Выполняя интегрирование, получим уравнение равнопеременного движения

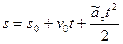. (1.37)

При этом скорость точки определяется формулой (1.35).

Выше полученные результаты можно свести в таблицу:

			Характер движения
	≠0 ≠0	≠0 ≠0	Прямолинейное и равномерное Прямолинейное и неравномерное Криволинейное и равномерное Криволинейное и неравномерное

ΙΙ. Простейшие движения твердого тела

Как и в статике, все тела, рассматриваемые в кинематике, считаются абсолютно твердыми, т. е. расстояния между двумя точками тела не изменяется при движении тела. Задачи кинематики твердого тела распадаются на две части:

— задание движения и определение кинематических характеристик движения тела в целом;

— определение кинематических характеристик (траекторий, скоростей и ускорений) всех точек тела.

Общей задачей кинематики твердого тела является изучение произвольного движения тела. Но прежде чем перейти к изучению этой общей задачи, сначала изучают простые, частные случаи движения, которые позволяют затем перейти к общему случаю движения. Эти частные случаи движения сами по себе также представляют интерес, так как часто встречаются при решении конкретных задач. Различают четыре частных случая движения твердого тела:

— поступательное;

— вращательное;

— плоское, или плоскопараллельное;

— сферическое.

Поступательное и вращательное движения являются простейшими движениями твердого тела.

2.1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА.

Поступательным движением твердого тела называется такое движение, при котором любая прямая, проведенная в теле, остается во все время движения тела параллельной своему начальному положению.

Говоря о траекториях точек тела при его поступательном движении, не следует считать их прямолинейными. При поступательном движении точки тела могут описывать любые криволинейные траектории.

Теорема. Все точки твердого тела, движущегося поступательно, описывают одинаковые (совпадающие при наложении) траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.

Дата добавления: 2014-11-06