Конформные отображения. Элементарные функции комплексного переменного 2 страница

Согласно свойству 4° значение w =0 не принимается ни при каком z. Следовательно, начало координат плоскости (w) не принадлежит к образу конечной плоскости (z). Любая точка w ¹0 принадлежит к образу плоскости (z). Действительно, так как

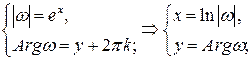
то прообразом точки w могут быть только точки 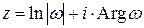. Их бесконечно много, т.к. Arg w имеет бесконечное множество значений, и каждая из этих точек есть прообраз точки w:

.

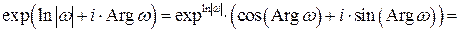
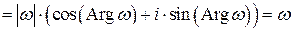Итак, функция exp z отображает конечную плоскость (z) на плоскость (w), из которой исключена точка w =0, причём отображение не взаимно-однозначно (доопределить exp z в точке нельзя, т.к. не существует 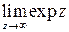). Так как 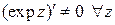, то отображение конформно в .

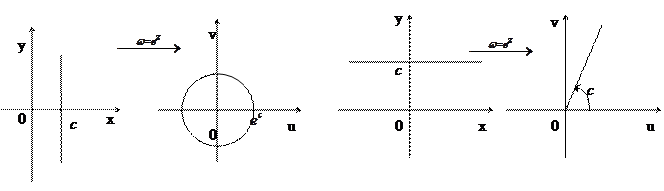При отображении 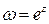совокупность прямых, параллельных мнимой оси, переходит в совокупность окружностей с центром в начале координат, а совокупность прямых, параллельных действительной оси, – в совокупность лучей, выходящих из начала координат.

Итак, при отображении 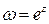декартова сетка координат на плоскости (z) переходит в полярную сетку координат на плоскости (w).

Пример. Найти образ полосы 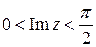при отображении .

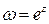■ 1. Найдем образ границы при заданном отображении. Она состоит из двух прямых: Im z =0 (действительная ось) и .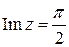

Найдем образ прямой Im z =0. Подставляя у =0 в соотношение 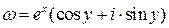, получим w=e^x (cos0+ i sin0), то есть Это уравнение положительной части действительной оси.

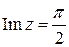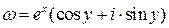Найдем образ прямой . При из соотношения получим , то есть Это уравнение положительной части мнимой оси.

2. Возьмем произвольную точку из данной полосы, например . Ее образом является точка 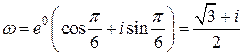, которая принадлежит первой четверти. Следовательно, образом полосы 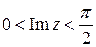при отображении 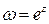является первая четверть w -плоскости. ■

4. Тригонометрические и гиперболические функции

Косинусом комплексного переменного z называется функция

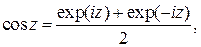
Синусом комплексного переменного z называется функция

.

Свойстваcos z и sin z

1° При 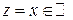cos z и sin z принимают действительные значения, совпадающие соответственно с cos x и sin x.

2° Из определения следует, что cos(- z)=cos z, sin(- z)=sin z, следовательно cos z – чётная, sin z – нечётная.

3° cos z и sin z – периодические с основным периодом 2 p.

4° Для sin z и cos z справедливы основные формулы тригонометрии.

5° cos z =0 при , sin z =0 при .

6° Особым свойством синуса и косинуса комплексного переменного является то, что эти функции неограниченные: .

7° Функции cos z и sin z аналитические в .

, .

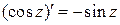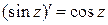Для функций e^z, sin z, cos z имеет место формула Эйлера:

e^iz =sin z + i cos z.

Тангенсом комплексного переменного z называется функция .

Котангенсом комплексного переменного z называется функция .

Свойства tg z и ctg z

1° , .

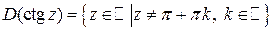2° tg z =tg x, ctg z =ctg x при .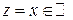

3° tg(- z)=-tg z, ctg(- z)=-ctg z .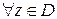

4° tg z и ctg z – периодические с основным периодом p.

5° Нули tg z совпадают с нулями sin z, нули ctg z – с нулями cos z.

6° tg z и ctg z – аналитические в своих областях определения,

, .

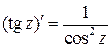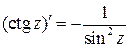7° tg z и ctg z принимают любые значения из , кроме z = i и z =- i.

Гиперболические функции комплексного переменного определяются следующим образом: , ,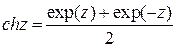

.

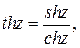
Зависимость между тригонометрическими и гиперболическими функциями выражается формулами:

cos(iz)=ch z, sin(iz)= i ×sh z. (4.1)

Пример. Найти значение модуляфункции w =sin z в точке .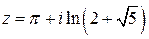

■ Пусть z=x+iy. Запишем заданное число в алгебраической форме. Используя известную тригонометрическую формулу, получим:

w =sin(x + iy)=sin x cos(iy)+cos x sin(iy).

Применим формулы (4.1): w =sin x ch y + i cos x sh y.

Тогда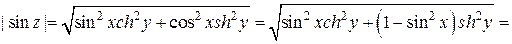

.

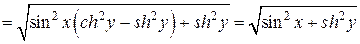Полагая 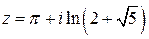, найдем

. ■

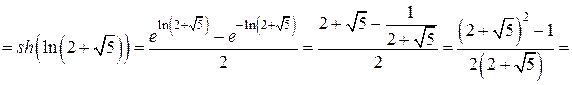
Этот пример показывает, что тригонометрическая функция sin z в комплексной области может принимать значения, по модулю большие единицы.

Пример. Записать число ch(2-3 i) в алгебраической форме.

■

■

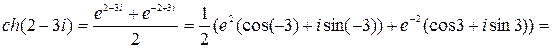
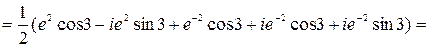
5. Степенная функция и радикал

Степенной называется функция вида .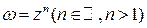

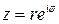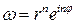Если , то . Или

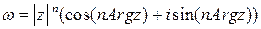
Функция обладает основными свойствами функции действительного переменного:

.

, при . Следовательно, – аналитическая в функция.

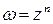–многолистная функция. Областями однолистности функции являются углы с вершиной в начале координат и раствором :

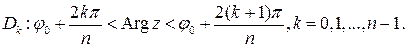
Если 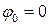, то

.

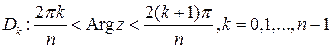Радикал 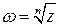определяется как функция, обратная к степенной 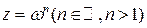. Пусть 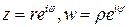т.е. , тогда

.

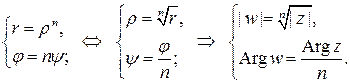Следовательно, радикал имеет n различных значений, которые выражаются формулой

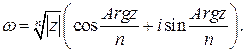
Функция 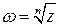является многозначной (n – значной). Эти n значений располагаются в вершинах правильного n – угольника, вписанного в окружность . При и получаем по одному значению функции w =0 и .

Чтобы выделить однозначную ветвь, достаточно указать, в какой области однолистности изменяется w. Областью однолистности функции 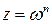является угол с вершиной в начале координат и раствором :

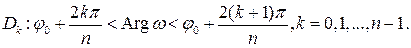
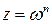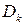Любой луч плоскости (w) при отображении переходит в луч плоскости (z): . Если луч пробегает область против хода часовой стрелки, то луч пробежит всю плоскость (z) от до . Следовательно, любая из областей однолистности 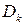перейдет в одну и ту же область плоскости (z): угол раствора 2π, границей которой служит луч .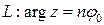

Таким образом, в области получаем n однозначных ветвей функции . Каждая из них определяется условием, что ее значения 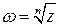принадлежат области D_k. Будем обозначать эти ветви .

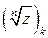6. Логарифмическая функция

Как было сказано, множество всех корней уравнения w=e^z (w ¹0) представляется формулой

z =ln| w |+ i Arg w, .

Значит, функция, обратная к z = e^w=e^u (cos v + i sin v), определена " z ¹0, " z ¹¥ и задается формулой

w =ln| z |+ i Arg z.

Она называется логарифмической и обозначается Ln z:

w =Ln z =ln| z |+ i Arg z= ln| z |+ i (аrg z +2 pk). (4.2)

Эта функция является многозначной. Главным значением Ln z называется то значение, которое получается при k =0, оно обозначается ln z:

ln z =ln| z |+ i arg z.

Тогда Ln z =ln z +2 kpi, .

Следовательно, любое комплексное число z ¹0, z ¹¥имеет бесконечное множество логарифмов (значений логарифмической функции), из которых любые два отличаются на целое кратное 2 p. Если 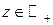, то Ln z =ln| z | . Но для этих 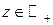существует еще бесконечно много значений логарифма. Например, Ln2=ln2+2 kpi, .

Свойства логарифмической функции

1° Ln(z ₁ z ₂)=Ln z ₁+Ln z ₂.

2° .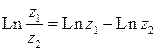

Замечание. Эти равенства означают равенство множеств (в том смысле, что множества состоят из одних и тех же элементов).

Поэтому, например, Ln z ² 2Ln z.

Введение понятия логарифма комплексного числа позволяет решать в комплексной области показательные уравнения. Простейшим таким уравнением является уравнение вида e^z+a =0. Его решение сводится к нахождению значений выражения Ln(-a), то есть z =Ln(-a).

Пример. Решить уравнение e^z +2 i =0.

■ Из равенства e^z =-2 i находим z =Ln(-2 i). Находим модуль и главное значение аргумента числа (-2 i): |-2 i |=2, 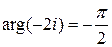. Следовательно, . ■

Чтобы выделить однозначные ветви функции w =Ln z, надо выделить области однолистности функции z=e^w. Ими являются полосы шириной 2 p, паралельные действительной оси:

D_k: v ₀+2 kπ <Im w < v ₀+2(k +1) π, .

Функция z =exp w однозначна на D_k, следовательно, здесь она имеет однозначначную обратную функцию w =(Ln z) _k многозначной функции w =Ln z. При отображении z =exp w прямая v=с переходит в луч z =exp(u +i v)= e^u (cos c +sin c), расположенный под углом С к действительной оси. Если прямая v=с проходит область D_k от v ₀+2 kπ до v ₀+2(k +1) π, то луч сделает полный оборот вокруг начала координат. Следовательно, образом полосы D_k является область G -угол раствора 2 p, границей которого служит луч, расположенный под углом v ₀ к действительной оси.

Таким образом, в области G получаем бесконечное множество различных однозначных ветвей функции w =Ln z. Каждая из w =(Ln z) _к характеризуется тем, что её значения принадлежат полосе D_k.

7. Общие степенная и показательная функции

Общей степенной функцией комплексной переменного называется функция вида

= exp(a Ln z), 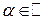. (4.3)

Она определена " z ¹0 и в общем случае является многозначной. Ее главное значение равно .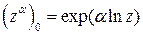

Функция вида

, (4.4)

где , , называется общей показательной функцией. Эта функция многозначна в силу многозначности Ln a. Ее главное значение равно .

Пример. Вычислить .

Решение.

Положим 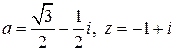. Применим формулы (4.4) и (4.2):

, .

,

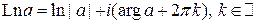Точка а лежит в четвертой четверти, следовательно,

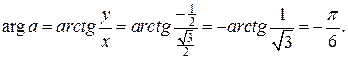
Тогда .

Окончательно получим:

.

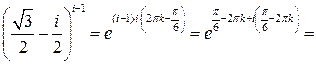
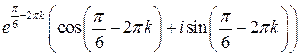Запишем ответ в алгебраической форме:

.

Дата добавления: 2014-11-06