
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Симплексный метод решения задачи линейного программирования
|
|
|
|
Графический метод решения задачи линейного программирования
Постановка задачи линейного программирования
Задача линейного программирования

Любое неотрицательное решение системы уравнений (3.1.1) называют допустимым решением, а допустимое решение, при котором целевая функция (3.1.3) принимает наибольшее (наименьшее) значение называют оптимальным решением задачи линейного программирования (3.1.1)-(3.1.3)





Для иллюстрации графического метода решения задачи линейного программирования рассмотрим следующий пример.











Симплекс-метод был разработан и впервые применен для решения задач в 1947 г. американским математиком Дж. Данцигом.
Симплексный метод в отличие от геометрического универсален. С его помощью можно решить любую задачу линейного программирования.
В основу симплексного метода положена идея последовательного улучшения получаемого решения.
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (или, по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение - вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).
Таким образом, имея систему ограничений, приведенную к канонической форме (все функциональные ограничения имеют вид равенств), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то осуществляется переход к другому, обязательно допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении целевая функция, если и не достигнет оптимума, то приблизится к нему (или, по крайней мере, не удалится от него). С новым допустимым базисным решением поступают так же, пока не отыщется решение, которое является оптимальным.
|
|
|
Процесс применения симплексного метода предполагает реализацию трех его основных элементов:
1) способ определения какого-либо первоначального допустимого базисного решения задачи;
2) правило перехода к лучшему (точнее, не худшему) решению;
3) критерий проверки оптимальности найденного решения.
Симплексный метод включает в себя ряд этапов и может быть сформулирован в виде четкого алгоритма (четкого предписания о выполнении последовательных операций). Это позволяет успешно программировать и реализовывать его на ЭВМ. Задачи с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную.
Реализация симплекс-алгоритма включает восемь шагов. Опишем их, параллельно рассматривая пример выполнения каждого шага в применении к задаче о хоккейных клюшках и шахматных наборах.
Компания специализируется на выпуске хоккейных клюшек и наборов шахмат. Каждая клюшка приносит компании прибыль в размере $2, а каждый шахматный набор - в размере $4. На изготовление одной клюшки требуется четыре часа работы на участке A и два часа работы на участке B. Шахматный набор изготавливается с затратами шести часов на участке A, шести часов на участке B и одного часа на участке C. Доступная производственная мощность участка A составляет 120 н-часов в день, участка В - 72 н-часа и участка С - 10 н-часов.
Сколько клюшек и шахматных наборов должна выпускать компания ежедневно, чтобы получать максимальную прибыль?
Условия задач указанного класса часто представляют в табличной форме (см. таблицу 2.1).
|
|
|
Таблица 2.1 - Исходные данные задачи об использовании производственных ресурсов
| производственные участки | затраты времени на единицу продукции, н-час | доступный фонд времени, н-час | |
| клюшки | наборы шахмат | ||
| А | |||
| В | |||
| С | - | ||
| прибыль на единицу продукции, $ | 4 |
Шаг 1. Формулировка ЗЛП (формирование целевой функции и системы ограничений).
Для определенности будем считать, что решается задача на отыскание максимума.
Сначала приведем общую постановку такой задачи.
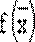 = c1x1 + c2x2 +... + cnxn −>max; = c1x1 + c2x2 +... + cnxn −>max;
| ||||
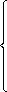
| a11x1 + a12x2 +... + a1nxn ≤ b1, a21x1 + a22x2 +... + a2nxn ≤ b2, ... am1x1 + am2x2 +... + amnxn ≤ bm; | |||
xj ≥ 0, j=1, ….., n
Повторим формулировку задачи для нашего примера.
 = 2x1 + 4x2 → max;
= 2x1 + 4x2 → max;
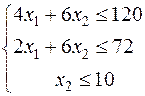
x1 ≥ 0, x2 ≥ 0.
Шаг 2. Приведение задачи к канонической форме (перевод функциональных ограничений в систему уравнений).
Для реализации шага в ограничения задачи вводятся дополнительные переменные. Ниже приведен порядок выполнения этой операции.
Введем дополнительные переменные y1, y2, …. ym.
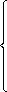
| a11x1 + a12x2 +... + a1nxn + y1 = b1, a21x1 + a22x2 +... + a2nxn + y2 = b2, ... am1x1 + am2x2 +... + amnxn + ym = bm. |
Обозначим добавочные переменные несколько иначе, а именно: y1 = xn+1, y2 = xn+2,..., ym = xn+m, где n - число переменных в исходной задаче, m - число уравнений.
Все дополнительные переменные также должны быть неотрицательными.
В отношении добавочных переменных нужно сделать еще одно важное замечание. Все они должны иметь тот же знак, что и свободные члены системы ограничений. В противном случае используется так называемый M-метод (метод искусственного базиса).
Выполним второй шаг для нашего примера.
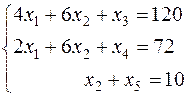
Шаг 3. Построение исходной симплекс-таблицы (получение первоначального допустимого базисного решения).
При ручной реализации симплексного метода удобно использовать так называемые симплексные таблицы. Исходная симплекс-таблица соответствует первоначальному допустимому базисному решению. В качестве такового проще всего взять базисное решение, в котором основными являются дополнительные переменные xn+1, xn+2,..., xn+m. Запишем исходную симплексную таблицу в общем виде (таблица 2.4)
|
|
|
Таблица 2.4 - Общий вид исходной симплекс-таблицы
| базис | переменные | bi | ||||||
| x1 | x2 | ... | xn | xn+1 | ... | xn+m | ||
| xn+1 | a11 | a12 | ... | a1n | b1 | |||
| xn+2 | a21 | a22 | ... | a2n | ... | b2 | ||
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| xn+m | am1 | am2 | ... | amn | bm | |||
| cj | c1 | c2 | ... | cn | L |
В левом столбце записываются основные (базисные) переменные, в первой строке таблицы перечисляются все переменные задачи. Крайний правый столбец содержит свободные члены системы ограничений b1, b2,..., bm. В последней строке таблицы (она называется оценочной) записываются коэффициенты целевой функции, а также значение целевой функции (с обратным знаком) при текущем базисном решении 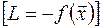 . В рабочую область таблицы (начиная со второго столбца и второй строки) занесены коэффициенты aij при переменных системы ограничений.
. В рабочую область таблицы (начиная со второго столбца и второй строки) занесены коэффициенты aij при переменных системы ограничений.
Запишем исходную симплексную таблицу в применении к рассматриваемой нами задаче (таблица 2.5). В данном случае переменные x3, x4 и x5 представляют собой запасы не реализованных производственных мощностей.
Таблица 2.5 - Исходная симплекс-таблица для задачи о хоккейных клюшках и шахматных наборах
| базис | переменные | bi | ||||
| x1 | x2 | x3 | x4 | x5 | ||
| x3 | ||||||
| x4 | ||||||
| x5 | ||||||
| cj |
Воспользуемся тем, что правые части всех уравнений нашей системы неотрицательны, а сама система имеет предпочитаемый вид – дополнительные переменные являются базисными. Приравняв к нулю свободные переменные x1 и x2, получаем базисное неотрицательное решение:
x1=0, x2=0, x3=120, x4=72, x5=10
Первые две компоненты этого решения представляют производственную программу  , по которой пока ничего не производится.
, по которой пока ничего не производится.
Таким образом, в данном базисном решении неосновные переменные x1 и x2 равны нулю. Базисные переменные отличны от нуля: x3 = 120, x4 = 72, x5 = 10. Данное базисное решение является допустимым. Естественно, что значение целевой функции в этом случае равно нулю, так как в формировании целевой функции участвуют переменные, которые для данного базисного решения являются неосновными.
|
|
|
Шаг 4. Проверка условия: все cj ≤ 0. Если НЕТ - осуществляется переход к шагу 5, если ДА - задача решена. Таким образом, на данном шаге проверяется наличие положительных элементов в последней строке симплексной таблицы. Если такие элементы имеются, необходимо продолжать решение.
В нашей задаче последняя строка содержит два положительных элемента, следовательно, необходимо перейти к шагу 5.
Шаг 5. Выбор разрешающего столбца (переменной, вводимой в базис). Разрешающий столбец выбирается в соответствии со следующим условием:
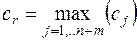
где r - номер разрешающего столбца.
Таким образом, при определении разрешающего столбца просматривается последняя строка симплексной таблицы и в ней отыскивается наибольший положительный элемент.
В нашей задаче в качестве разрешающего выберем второй столбец (соответствующий переменной x2), поскольку в последней строке для этого столбца содержится 4.
Шаг 6. Проверка условия: все air ≤ 0. Если ДА - целевая функция неограничена и решения нет, если НЕТ - переход к шагу 7.
Таким образом, необходимо проверить элементы разрешающего столбца. Если среди них нет положительных, то задача неразрешима.
В нашей примере все элементы разрешающего столбца положительны (6, 6 и 1), следовательно, необходимо перейти к шагу 7.
Шаг 7. Выбор разрешающей строки (переменной, выводимой из базиса) по условию:
 для air > 0,
для air > 0,
где s - номер разрешающей строки.
Таким образом, для тех строк, где элементы разрешающего столбца положительны, необходимо найти частное от деления элемента bi (последний столбец таблицы) на элемент, находящийся в разрешающем столбце. В качестве разрешающей выбирается строка, для которой результат такого деления будет наименьшим. Элемент, стоящий на пересечении разрешающей строки и разрешающего столбца, называется разрешающим элементом.
Выполним шаг 7 для нашей задачи.
Для первой строки: D1 = 120 / 6 = 20.
Для второй строки: D2 = 72 / 6 = 12.
Для третьей строки: D3 = 10 / 1 = 10.
Наименьший результат деления - в третьей строке, значит именно эту строку мы выбираем в качестве разрешающей, т.е. исключать из базисного решения будем переменную x5.
В нашем случае разрешающим элементом является единица, стоящая на пересечении третьей строки и второго столбца.
Исходная симплекс-таблица нашего примера с выделенными цветом разрешающей строкой и разрешающим столбцом представлена ниже (таблица 2.6).
Таблица 2.6 - Исходная симплекс-таблица с выделенными разрешающей строкой и столбцом, а также с иллюстрацией к применению правила прямоугольника

Шаг 8. Пересчет элементов симплекс-таблицы (переход к новому базисному решению). Порядок пересчета различных элементов таблицы несколько отличается.
Для элементов разрешающей строки используются следующие формулы:
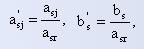
где s - номер разрешающей строки,
r - номер разрешающего столбца,
 ,
, 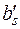 - новые значения пересчитываемых элементов,
- новые значения пересчитываемых элементов,
asj, bs - старые значения пересчитываемых элементов,
a sr - старое значение разрешающего элемента.
Таким образом, при пересчете элементов разрешающей строки каждый ее элемент делится на разрешающий элемент.
Еще проще пересчитать элементы разрешающего столбца. Все они (кроме разрешающего элемента) становятся равными нулю:
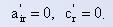
Элементы, не принадлежащие разрешающим столбцу и строке, пересчитываются по так называемому правилу прямоугольника: мысленно выделяется прямоугольник, в котором элемент, подлежащий пересчету и разрешающий элемент образуют одну из диагоналей. Формулы будут иметь следующий вид:
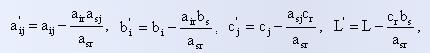
где  ,
, 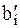 ,
,  , L' - новые значения пересчитываемых элементов,
, L' - новые значения пересчитываемых элементов,
aij, bi, cj, L - старые значения пересчитываемых элементов.
По окончании пересчета осуществляется возврат к шагу 4.
Применение правила прямоугольника для элемента, не принадлежащего разрешающим столбцу и строке проиллюстрируем, используя таблицу 2.6. Пересчитаем элемент a11 (в исходной симплекс-таблице его значение равно 4). В таблице 2.6 можно видеть прямоугольник (прочерчен пунктиром), соединяющий четыре элемента, участвующих в пересчете:

Аналогичным образом пересчитываются остальные элементы.
Полностью результат пересчета для нашего примера можно видеть в таблице 2.7
Таблица 2.7 - Симплекс-таблица для задачи о хоккейных клюшках и шахматных наборах (второе базисное решение)
| базис | переменные | bi | ||||
| x1 | x2 | x3 | x4 | x5 | ||
| x3 | -6 | |||||
| x4 | -6 | |||||
| x2 | ||||||
| cj | -4 | -40 |
Оценки базисных векторов всегда равны нулю. Таким образом, в новом базисном решении базисными переменными являются: x2 = 10, x3 = 60, x4 = 12 (соответствующие значения можно видеть в последнем столбце таблицы). Неосновные переменные x1 и x5 равны нулю. Значение целевой функции в этом случае равно 40 (значение можно видеть в правой нижней ячейке таблицы).
Доведем решение нашего примера до конца.
Вернемся к шагу 4 симплекс-алгоритма. Рассмотрим последнюю строку таблицы 2.7. В ней есть положительные элементы, значит, полученное решение не является оптимальным.
Шаг 5. Выберем разрешающий столбец. Им окажется столбец x1, поскольку здесь содержится единственный положительный элемент нижней строки. Соответственно, переменную x1 будем переводить в основные.
Шаг 6. Проверка показывает, что в разрешающем столбце есть положительные элементы, следовательно, можно продолжать решение.
Шаг 7. Определим разрешающую строку. При этом будем рассматривать лишь первую и вторую строки, поскольку для третьей строки в разрешающем столбце находится нуль. Найдем частное от деления элемента bi на элемент, находящийся в разрешающем столбце:
Для первой строки: D1 = 60 / 4 = 15.
Для второй строки: D2 = 12 / 2 = 6.
Наименьший результат деления - во второй строке, значит именно эту строку мы выбираем в качестве разрешающей, т.е. переводить в неосновные (исключать из базиса) будем переменную x4. (Она во второй строке).
Ниже приведена симплекс-таблица с выделенными разрешающей строкой и столбцом (таблица 2.8).
Таблица 2.8 - Симплекс-таблица (второе базисное решение) с выделенными разрешающей строкой и столбцом
| базис | переменные | bi | ||||
| x1 | x2 | x3 | x4 | x5 | ||
| x3 | -6 | |||||
| x4 | -6 | |||||
| x2 | ||||||
| cj | -4 | -40 |
Далее перейдем к шагу 8 и осуществим пересчет элементов симплексной таблицы в соответствии с правилами, приводимыми выше. Результат пересчета представлен в таблице 2.9.
Таблица 2.9 - Симплекс-таблица для задачи о хоккейных клюшках и шахматных наборах (третье базисное решение)
| базис | переменные | bi | ||||
| x1 | x2 | x3 | x4 | x5 | ||
| x3 | -2 | |||||
| x1 | 1/2 | -3 | ||||
| x2 | ||||||
| cj | -1 | -52 |
Таким образом, в очередном (третьем) базисном решении основными переменными являются: x1 = 6, x2 = 10, x3 = 36. Неосновные переменные x4 и x5 равны нулю. Значение целевой функции для этого решения равно 52.
Вернемся к шагу 4 симплекс-алгоритма. Рассмотрим последнюю строку таблицы 2.9. В ней все еще есть положительные элементы, значит полученное решение не является оптимальным, и необходимо продолжить выполнение симплекс-алгоритма.
Шаг 5. Выберем разрешающий столбец. Им окажется столбец x5, поскольку здесь содержится единственный положительный элемент нижней строки. Переменную x5 будем переводить в основные.
Шаг 6. Проверка показывает, что в разрешающем столбце есть положительные элементы, следовательно, можно продолжать решение.
Шаг 7. Определим разрешающую строку. При этом будем рассматривать лишь первую и третью строки, поскольку для второй строки в разрешающем столбце находится отрицательное число. Найдем частное от деления элемента bi на элемент, находящийся в разрешающем столбце:
Для первой строки: D1 = 36 / 6 = 6.
Для третьей строки: D2 = 10 / 1 = 10.
Наименьший результат деления - в первой строке, значит именно эту строку мы выбираем в качестве разрешающей, т.е. переводить в неосновные (исключать из базиса) будем переменную x3.
Запишем симплекс-таблицу с выделенными разрешающей строкой и столбцом (таблица 2.10).
Таблица 2.10 - Симплекс-таблица (третье базисное решение) с выделенными разрешающей строкой и столбцом
| базис | переменные | bi | ||||
| x1 | x2 | x3 | x4 | x5 | ||
| x3 | -2 | |||||
| x1 | 1/2 | -3 | ||||
| x2 | ||||||
| cj | -1 | -52 |
Далее перейдем к шагу 8 и осуществим пересчет элементов симплексной таблицы в соответствии с правилами, приводимыми выше. Результат пересчета представлен в таблице 2.11.
Таблица 2.11 - Симплекс-таблица для задачи о хоккейных клюшках и шахматных наборах (четвертое базисное решение)
| базис | переменные | bi | ||||
| x1 | x2 | x3 | x4 | x5 | ||
| x5 | 1/6 | -1/3 | ||||
| x1 | 1/2 | -1/2 | ||||
| x2 | -1/6 | 1/3 | ||||
| cj | -1/3 | -1/3 | -64 |
Таким образом, в очередном (четвертом) базисном решении основными переменными являются: x1 = 24, x2 = 4, x5 = 6. Неосновные переменные x3 и x4 равны нулю. Значение целевой функции для этого решения равно 64.
Вернемся к шагу 4. Рассмотрим последнюю строку таблицы 2.11. Положительных элементов в ней не осталось, следовательно полученное решение является оптимальным. Решение задачи найдено.
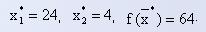
На рисунке 2.2 приведена общая схема симплексного алгоритма, наглядно показывающая порядок его реализации.

|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 4002; Нарушение авторских прав?; Мы поможем в написании вашей работы!