
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введение в матаматический анализ
|
|
|
|
Если определитель системы уравнений то такая система уравнений имеет одно определенное решение, получаемое по формулам
 (3)
(3)
Формулы (3) называются формулами Крамера, где Δхi получается заменой i-го столбца в главном определителе Δ столбцом свободных членов.
Если определитель системы Δ=0 и по крайней мере один из определителей  , то такая система уравнений не имеет решения. Если же Δ=0 и все Δхi=0, то данная система уравнений либо не имеет решения, либо имеет бесчисленное множество решений.
, то такая система уравнений не имеет решения. Если же Δ=0 и все Δхi=0, то данная система уравнений либо не имеет решения, либо имеет бесчисленное множество решений.
Определитель данной системы 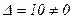 .
.
Вычислим вспомогательные определители:

Применяя формулы (3), находим:

Пример 1. Дано комплексное число  , требуется:
, требуется:
2) записать число а в алгебраической и тригонометрической формах;
3) найти все корни уравнения z3 + a = 0,  .
.
Решение.
1) Комплексным числом называется выражение
z = a + вi (1)
где а и в, действительные числа, а i – мнимая единица, которая определяется равенством i2=-1,  ; а – действительная часть числа z, в – мнимая часть числа z. Равенство (1) называется алгебраической формой записи. Числа а + вi и а – вi, отличающиеся только знаком мнимой части, называются сопряженными комплексными числами. Умножим число а на множитель, сопряженным знаменателем:
; а – действительная часть числа z, в – мнимая часть числа z. Равенство (1) называется алгебраической формой записи. Числа а + вi и а – вi, отличающиеся только знаком мнимой части, называются сопряженными комплексными числами. Умножим число а на множитель, сопряженным знаменателем:
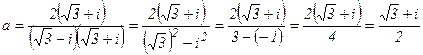
Таким образом, имеем: 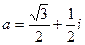 - алгебраическая форма записи комплексного числа а.
- алгебраическая форма записи комплексного числа а.
Всякое комплексное число z = a + вi можно изобразить на плоскости хОу, в виде точки А(а; в); 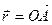 - начало его в точке О(0; 0), а конец в точке А(а; в).
- начало его в точке О(0; 0), а конец в точке А(а; в).
Точками, лежащими на оси Ох, соответствуют действительные числа (в=0).
Если же точка расположена на оси Оу, то она изображает чисто мнимое число, так как а=0. Поэтому ось Оу называют осью мнимых чисел или мнимой осью, а ось Ох – действительной осью.
|
|
|

Рис 1.
Исходя из рис.2 a = r cosφ, в = r sinφ, где r и φ – полярные координаты точки А(а; в). Тогда тригонометрическая форма записи числа запишется в следующем виде:
 или
или  (2)
(2)
Величины r и φ выражаются через а и в формулами

где 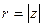 - модуль, φ = arg z – аргумент комплексного числа z, который определяется с точностью до 2πk, k = 0,
- модуль, φ = arg z – аргумент комплексного числа z, который определяется с точностью до 2πk, k = 0,  1,
1,  2, …
2, …
Для данного комплексного числа
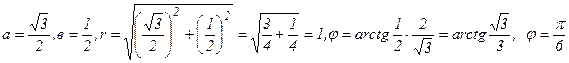
Таким образом, 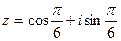 - тригонометрическая форма записи комплексного числа.
- тригонометрическая форма записи комплексного числа.
2) Представим уравнение  в виде
в виде 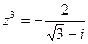 или
или  тогда
тогда 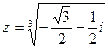 , т.е. задача сводится к вычислению всех значений
, т.е. задача сводится к вычислению всех значений 
Корень n – ой степени из комплексного числа z = r (cos φ + i sin φ) имеет n различных значений, которые находятся по формуле
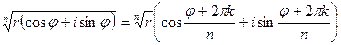 (3)
(3)
где 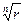 - арифметическое значение корня, а число k пробегает значения 0, 1, 2, …, n - 1.
- арифметическое значение корня, а число k пробегает значения 0, 1, 2, …, n - 1.
Запишем выражение -  в виде
в виде 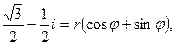 где
где 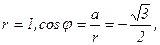

Можно считать, что угол φ принадлежит 3-й четверти; φ = 270˚-α, где α - угол в 1-ой координатной четверти. Имеем  тогда
тогда 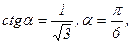
угол 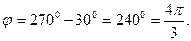
Итак,

Придавая k последовательно значения 0, 1, 2, получим соответственно числа z1, z2, z0.
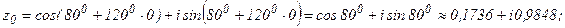
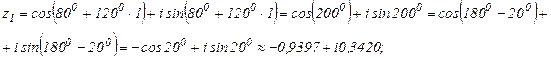

Пример 2. Если известен график функции у = f(x), то график функции вида у = kf(mx + b) + a можно построить последовательным преобразованием графика функции у = f(x).
Покажем, например, как с помощью таких преобразований можно построить график функции у = -2sin(2x + 2), исходя из известного графика функции у = sinx. От функции у = sinx к функции у = - 2sin(2x + 2) можно перейти с помощью следующей цепочки преобразований:
y1 = sin2x1, y2 = - 2sin2x2,
Y = - 2sin2(X + 1) = - 2sin(2X + 2).
Геометрически это приводит к следующим построениям (рис.2):
1) Строим одну волну синусоиды у = sinx;  .
.
2) Отмечаем на синусоиде несколько точек и уменьшаем в два раза их абсциссы, не изменяя ординат; таким образом мы отображаем точку (х; у) и точку (х1; у1), где х1 = х/2, у1 = у. Соединив полученные точки плавной линией, получим график функции у1 = sin2x1, являющийся результатом «сжатия» графика функции у = sinx к оси Оу в два раза.
|
|
|
3) Увеличиваем ординаты точек, построенных в предыдущем пункте в два раза, а затем меняем их знаки на противоположные, не изменяя абсцисс; таким образом отображаем точку (х1;у1) в точку (х2; у2), где у2 = - 2у1, х2 = х1. Соединив полученные точки плавной линией, получим график функции у2 = - 2sin2x2, являющейся результатом «растяжения» графика функции у1 = sin2x1 от оси Ох в два раза с последующим зеркальным отражением графика от оси Ох.
4) Переносим точки, построенные в предыдущем пункте, на –1 в направлении оси Ох (т.е. на единицу влево); таким образом мы отображаем точку (х2; у2) в точку (Х; Y), где Х = х2 - 1, Y = у2. Соединив полученные точки плавной линией, получим график функции Y = -2sin 2(X + 1) = - 2sin (2X + 2), являющийся результатом «сдвига» графика функции у2 = - 2sin 2х2 на –1 в направлении оси Ох. Искомый график функции у = - 2sin (2x +2) построен.

Рис. 2.
Пример 3. Найти пределы функции не пользуясь правилом Лопиталя:
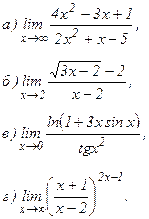
Решение.
а) Под знаком предела имеется дробная рациональная функция и при х→∞ получается неопределенность вида  . Чтобы найти предел дробной рациональной функции
. Чтобы найти предел дробной рациональной функции 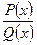 при х→∞, необходимо предварительно числитель и знаменатель дроби разделить на хn, где n – наивысшая степень многочленов Р(х) и Q(x). Разделим числитель и знаменатель данной дроби на х2 и применим основные теоремы о пределах и свойствах бесконечно малых величин:
при х→∞, необходимо предварительно числитель и знаменатель дроби разделить на хn, где n – наивысшая степень многочленов Р(х) и Q(x). Разделим числитель и знаменатель данной дроби на х2 и применим основные теоремы о пределах и свойствах бесконечно малых величин:
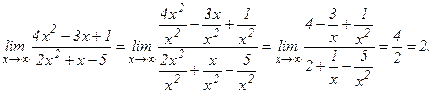
б) Непосредственная подстановка предельного значения аргумента х=2 приводит к неопределенности вида 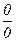 . Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму
. Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму 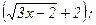

в) Непосредственная подстановка предельного значения аргумента х=0 приводит к неопределенности 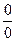 . Известно, что при нахождении предела отношения двух бесконечно малых величин можно каждую из них (или только одну) заменить другой бесконечно малой, ей эквивалентной.
. Известно, что при нахождении предела отношения двух бесконечно малых величин можно каждую из них (или только одну) заменить другой бесконечно малой, ей эквивалентной.
Так как при х→∞ ln(1 + x)~ x, tg x ~ x, то ln(1 + 3x sin x) ~3x sin x, tg x2~ x2 и 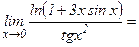
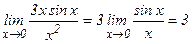
(используя 1-ый замечательный предел  ).
).
г) При х→∞ основание  стремится к 1, а показатель степени (2х – 1)→∞. Следовательно, имеем неопределенность вида 1∞. Для ее раскрытия будем использовать II замечательный предел
стремится к 1, а показатель степени (2х – 1)→∞. Следовательно, имеем неопределенность вида 1∞. Для ее раскрытия будем использовать II замечательный предел 
Представим основание в виде суммы: единицы и некоторой бесконечно малой величины:
|
|
|
 .
.
Тогда
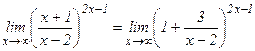 .
.
Положим х – 2 = 3у; при х → ∞ переменная у → ∞. Выразим показатель степени через новую переменную у. Так как х = 3у + 2, то 2х -1 = 2(3у + 2) – 1 = 6у + 3. Таким образом,

Пример 4. Дана функция у =161/(2+х). Требуется:
1) установить, является ли данная функция непрерывной или разрывной при значениях аргумента х1=-2, х2=0;
2) в случае разрыва функции найти ее пределы в точке разрыва справа и слева;
3) сделать схематический чертеж.
Решение.
Если ищется предел функции у=f(х) при условии, что аргумент х, стремясь к своему предельному значению а, может принимать только такие значения, которые меньше а, то этот предел, если он существует, называется левосторонним (левым) пределом данной функции в точке х = а и условно обозначается так:
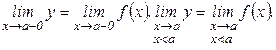
Если ищется предел функции у=f(х) при условии, что аргумент х, стремясь к своему предельному значению а, может принимать только такие значения, которые больше а, то этот предел если он существует, называется правосторонним (правым) пределом данной функции в точке х = а и условно обозначается так:

Функция у = f(х) непрерывна в точке х = а, если выполнимы следующие условия:
1) функция у = f(х) определена не только в точке а, но и в некотором интервале, содержащем эту точку;
2) функция у = f(х) имеет при х→а конечные и равные между собой односторонние пределы;
3) односторонние пределы при х → а совпадают со значением функции в точке а, т.е. 
Если для данной функция у = f(х) в данной точке х = а хотя бы одно из перечисленных условий не выполняется, то функция называется разрывной в точке х = а.
Разрыв функция у = f(х) в точке х = а называется разрывом первого рода, если существуют конечные односторонние пределы 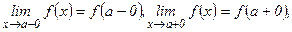 причем не все три числа f(a), f(a-0) и f(a+0) равны между собой.
причем не все три числа f(a), f(a-0) и f(a+0) равны между собой.
Если же хотя бы один из односторонних пределов не существует, то разрыв в точке х = а называется разрывом второго рода.
При х = -2, данная функция не существует: в этой точке функция терпит разрыв. Определим односторонние пределы функции при х = -2 слева и справа:
|
|
|
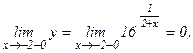
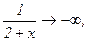 а
а 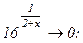

 и
и 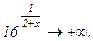
Таким образом, данная функция при х = -2 имеет разрыв второго рода. При х = 0 функция непрерывна, т.к. выполняются все три условные непрерывности функции.
Данная функция является показательной. Прямая х = -2 – вертикальная асимптота графика функции. Множество значений функции – множество всех положительных чисел. у = 1 – горизонтальная асимптота, т.к. 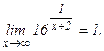
Чтобы построить функцию  , составим следующую таблицу:
, составим следующую таблицу:
| х | -10 | -6 | -4 | -3 | -1 | |||||
| у | 
| 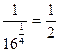
| 
| 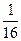
| 
| 
| 
| 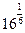
| 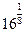
|
График функции показан на рис. 3.
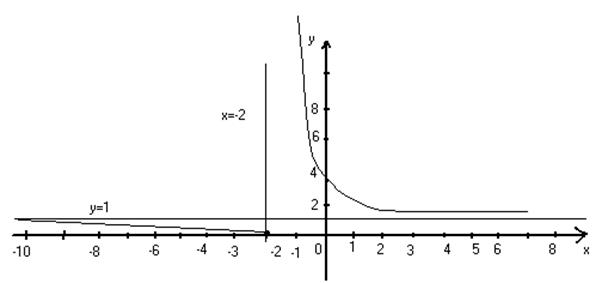
Рис. 3.
Пример 5. Задана функция y = f (х) различными аналитическими выражениями для различных областей изменения аргумента х:
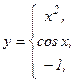
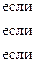

Найти: 1) точки разрыва функции, если они существуют;
2)предел функции у при приближении аргумента х к точке разрыва слева и справа;
3)найти скачок функции в точке разрыва.
Решение.
Данная функция определена и непрерывна в интервалах (-∞; 0), (0; π) и (π; + ∞). При х = 0 и х = π меняется аналитическое выражение функции и только в этих точках функция может иметь разрыв. Определим односторонние пределы в точке х = 0;
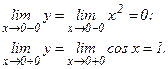
Так как односторонние пределы функции у в точке х = 0 не равны между собой, то в этой точке функция имеет разрыв первого рода.
Скачком функции в точке разрыва называется абсолютная величина разности между ее правым и левым предельными значениями. Следовательно, в точке х = 0 скачок функции Δ=|1 - 0|=1.
Определим односторонние пределы в точке х = π:
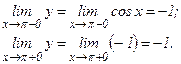
Односторонние пределы совпадают и функция в этой точке непрерывна.
График функции показан на рис. 4.
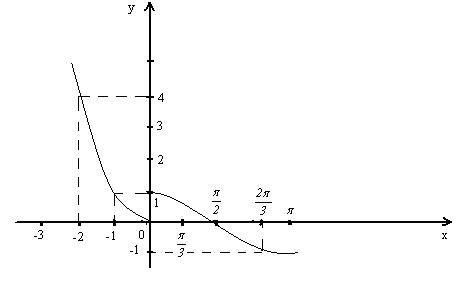
Рис. 4.
III. Производная и ее приложения
Основные правила и формулы дифференцирования:
1. y = c, где c=const, 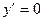 .
.
2. y = x, y'=1.
3. 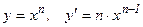 .
.
4.  .
.
5. 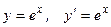 .
.
6.  .
.
7. 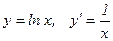 .
.
8. 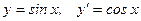 .
.
9. 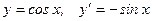 .
.
10.  .
.
11.  .
.
12. 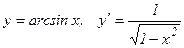 .
.
13. 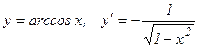 .
.
14. 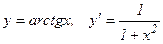 .
.
15. 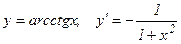 .
.
16. 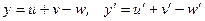 .
.
17. 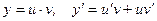 .
.
18.  .
.
19.  - это правило дифференцирования сложной функции.
- это правило дифференцирования сложной функции.
Пример 1. Найти производные  данных функций
данных функций
а) 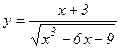 ; б)
; б) 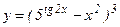 ;
;
в)  ; г)
; г)  <1;
<1;
д) 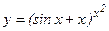 ; е)
; е)  .
.
Решение:
а) Применяя правило дифференцирования дроби и формулы (3); (16), имеем

б) Последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, имеем:

в) 
г) 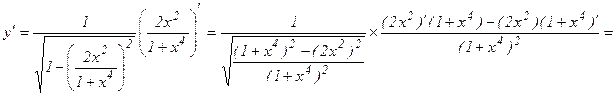

д) Предварительно прологарифмируем по основанию е обе части равенства:
 или
или 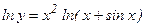 .
.
Теперь дифференцируем обе части, считая lny сложной функцией от переменной x.
 откуда
откуда
 .
.
е) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную y', надо продифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной y'. Имеем:
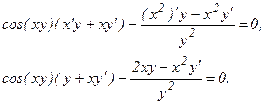
Из полученного равенства, связывающего х, у и y', находим производную y':
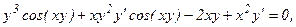
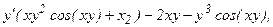 откуда
откуда 
Пример 2. Найти производную второго порядка  :
:
а) 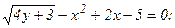
б) 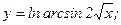
в) 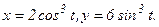
Решение: а) Функция у задана в неявном виде. Дифференцируем по х обе части заданного уравнения, считая при этом у функцией от х:
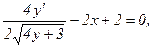 откуда
откуда 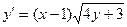 (1)
(1)
Снова дифференцируем по х обе части равенства (1):
 (2)
(2)
Заменив y' в (2) правой частью (1), получим
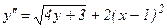 .
.
б) Найдем первую производную данной функции
 .
.
Найдем производную от первой производной, получим вторую производную функции  :
:
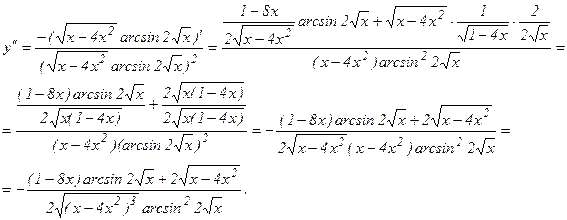
в) Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти производную y', находим сначала дифференциалы dy и dx и затем берем отношение этих дифференциалов:

Тогда 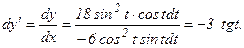
Производная второго порядка 
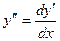 . Значит, чтобы найти y'', надо найти дифференциал dy':
. Значит, чтобы найти y'', надо найти дифференциал dy':
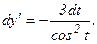
Тогда 
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 590; Нарушение авторских прав?; Мы поможем в написании вашей работы!