Краткие теоретические сведения. Решение главной геодезической задачи на поверхности эллипсоида

Решение главной геодезической задачи на поверхности эллипсоида

Решение сферического треугольника по способу аддитаментов

Идея способа аддитаментов заключается в том, что стороны сферического треугольника a,b,c исправляют поправками, в результате чего получают стороны плоского треугольника a’,b’,c’ и неизвестные стороны сферического треугольника. Аддитаментами являются величины A_a=ka³, A_b=kb³, A_c=kc³, где k=1/6R², R – средний радиус кривизны эллипсоида для района расположения треугольника. Значение величины можно принять постоянной для территории бывшего СССР и равной k=4.09×10^-15. При этом длины сторон треугольника выражают в метрах.

Последовательность решения по способу аддитаментов:

1) Из исходной стороны c вычитают ее аддитамент A_c и получают сторону плоского треугольника c’.

2) По известным углам сферического треугольника и стороне c’ решают треугольник как плоский, используя теорему синусов, и находят остальные стороны плоского треугольника a’ и b’: a’=c’sinA/sinC, b’=c’sinB/sinC

3) Полученные значения сторон исправляют их аддитаментами и находят искомые стороны сферического треугольника: a=a’+ka^’3=a’+A_a, b=b’+kb^’3=b’+A_b

Задание и исходные данные

Решить треугольник по теореме Лежандра и способу аддитаментов. Исходные данные: Bm =55°27'00''; S_AB=30500,123+100·№, где № – номер варианта; f=0,0025290; A = 50°20'19.41''; B = 62°12'44.54''; C = 67°26'58.43''

Схема решения

Bm =	55°27'00''		A B C a c b
c =	30 500,123
Углы треугольника на эллипсоиде
A =	50°20'19.41''
B =	62°12'44.54''
C =	67°26'58.43''
Теорема Лежандра
Вычисление сферического избытка
f	0,0025290
cкм^2	930,258
sinA	0,7698311
sinB	0,8846817
sinC	0,9235423
ε	1,735''

Решение треугольника
Вершина	Измеренные углы сферического треугольника	Поправка из уравнивания -w/3	Уравненные углы сферического треугольника	-ε/3	Углы плоского треугольника	Синусы углов плоского треугольника
С	67°26'58.43''	-0,215''	67°26'58.22''	-0,578''	67°26'57.64''	0,92354083
A	50°20'19.41''	-0,215''	50°20'19.20''	-0,578''	50°20'18.62''	0,76982865
B	62°12'44.54''	-0,215''	62°12'44.33''	-0,578''	62°12'43.75''	0,88467987
Σ	180°00'02.38''	-0,65''	180°00'01.74''	-1,73''	180°00'00.00''
ε	1,73''
w=Σ-180-ε	0,65''
Стороны сферического треугольника
DII	33 025,202
a	25 423,747
b	29 216,732

Способ аддитаментов (Схема решения)
k =	4,09E-15
Вершина	Измеренные углы сферического треугольника	Поправка из уравнивания -w/3	Уравненные углы сферического треугольника	Синусы уравненных углов сферического треугольника	Стороны плоского треугольника	As	Стороны сфероидического треугольника
С	67°26'58.43''	-0,215''	67°26'58.22''	0,92354191	30 500,007	0,116	30 500,123
A	50°20'19.41''	-0,215''	50°20'19.20''	0,76983044	25 423,680	0,067	25 423,747
B	62°12'44.54''	-0,215''	62°12'44.33''	0,88468118	29 216,630	0,102	29 216,732
Σ	180°00'02.38''	-0,65''
ε	1,73''
w	0,65''

Определение координат некоторой точки по известным координатам других точек к измеренным или заданным угловым к линейным величинам называется главной геодезической задачей.

Такая задача может быть поставлена в различных координатных системах. В высшей геодезии принято решать эту задачу в геодезической системе координат, которая предполагает известными размеры и ориентировку конкретного референц-эллипсоида.

Главную геодезическую задачу принято рассматривать в виде двух задач: прямой и обратной.

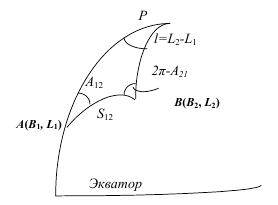Прямая геодезическая задача состоит в том, чтобы по известным координатам начальной точки B₁, L₁, прямому азимуту A₁₂ и расстоянию S₁₂ определить координаты конечной точки B₂, L₂ и обратный азимут A₂₁.

Обратная геодезическая задача заключается в том, чтобы по координатам начальной и конечной точек B₁, L₁, B₂, L₂ определить расстояние S₁₂ между ними и азимуты A₁₂, A₂₁ (см. рис).

В геодезической практике прямую и обратную геодезические задачи приходится решать для различных длин геодезических линий. На практике установилась определенная градация возможных расстояний, для каждой из которых существует наиболее удобный метод решения главных геодезических задач.

· Малые расстояния (от 20 до 200 км) встречаются при вычислении сторон треугольников и замыкающих звеньев триангуляции I класса.

· Средние расстояния (от 200 до 800 км) имеют место при вычислении диагоналей полигонов триангуляции 1 класса, при обработке астрономо-геодезической сети, при развитии динамической (ракетной) триангуляции, радиогеодезических сетей и других задач.

· Большие расстояния (более 800 км) встречаются при ориентировке референц-эллипсоида, при геодезическом соединении материков методом космической триангуляции, в радионавигации, при установлении единой координатной системы. в целях слежения за управляемыми ракетами и т. д.

Для решения главных геодезических задач необходимо установить уравнения связи исходных и определяемых величин. Наиболее простой и естественный способ установления таких уравнений связи и в конечном итоге решения главных геодезических задач заключается в непосредственном решении треугольника APB (см. рис.), в котором исходные данные и определяемые неизвестные как в прямой, так и в обратной задачах являются элементами этого треугольника. Например, в случае прямой геодезической задачи исходными данными являются стороны S₁₂, AP и угол A₁₂. Из решения треугольника получаются другие его элементы l, A₂₁, BP, с помощью которых определяют искомые величины L₂=L₁+l, B₂=90°–BP.

Такой путь решения главных геодезических задач называется прямым. Однако в связи с большими сторонами полярного треугольника APB, достигающими нескольких тысяч километров, его нужно рассматривать как сфероидический. Это обстоятельство значительно усложняет решение и требует использования 10-значных таблиц тригонометрических функций. Поэтому применяют другой путь решения, который называют косвенным.

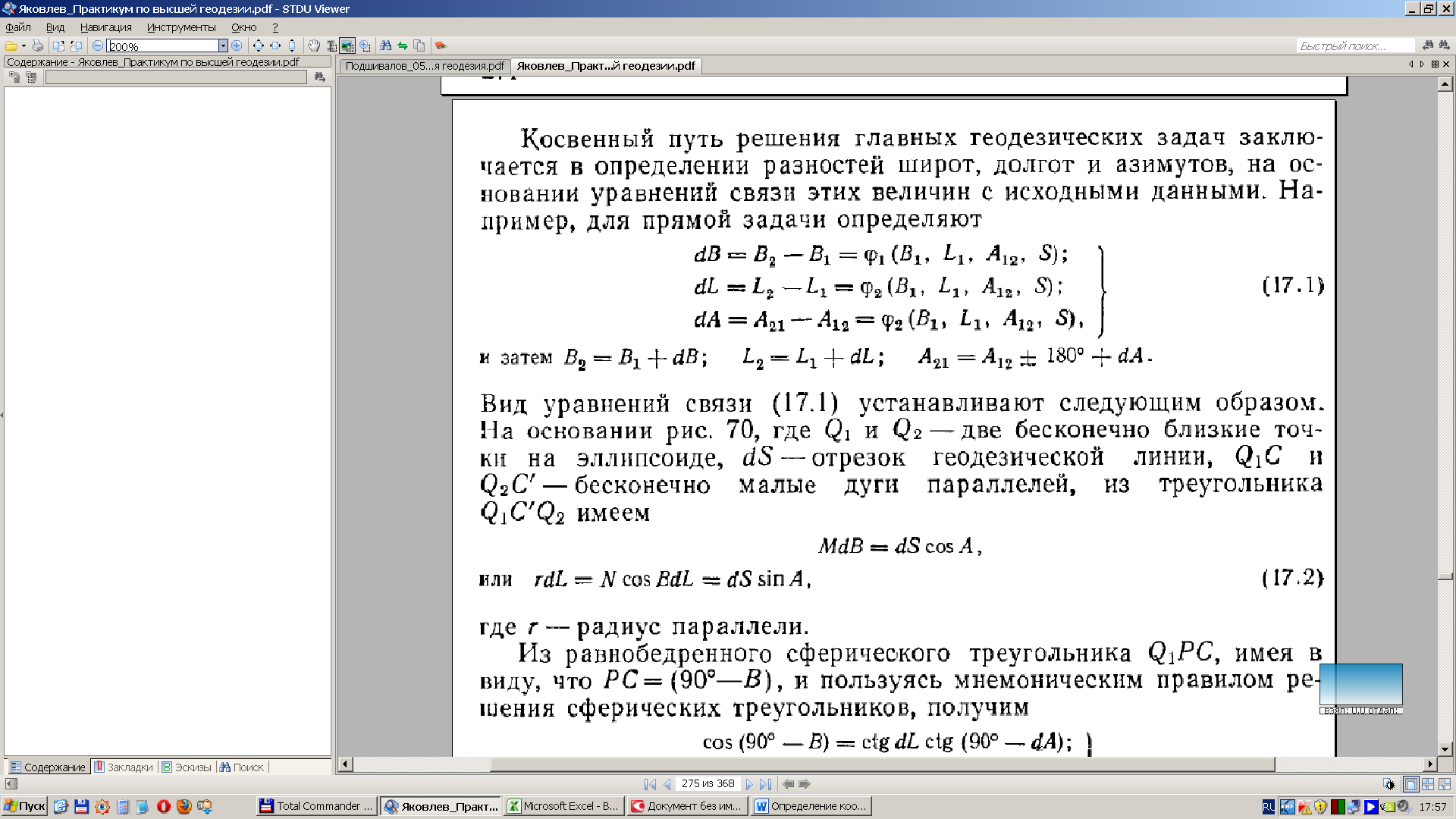
Косвенный путь решения главных геодезических задач заключается в определении разностей широт, долгот н азимутов, на основании уравнений связи этих величин с исходными данными. Например, для прямой задачи определяют

Задание и исходные данные

Прямая задача

В треугольнике ABC из решения прямой геодезической задачи вычислить геодезические координаты каждой вершины. Значения длин сторон и уравненных сферических углов треугольника взять из предыдущей работы (Решение геодезических треугольников).

Последовательность вычислений:

1) Используя B_A= 52°20'00.000'', L_A= 65°12'34.567'', A_AB= 12°34'56.789'' и сторону S_AB, согласно своего варианта в работе «Решение геодезических треугольников», получить из решения прямой геодезической задачи координаты точки B (B_{B ,} L_A) и обратный азимут А_BA.

2) Вычислить азимут стороны A_BC = A_BA – <B. Используя координаты точки B (B_{B ,} L_A), азимут A_BC , сторону S_BС , получить из решения прямой геодезической задачи координаты точки С (B_{C ,} L_C) и азимут A_CB.

3) Аналогично предыдущему этапу, получить азимут A_CА и вычислить для контроля координаты точки А и азимут A_АC, используя координаты точки С и сторону S_AС.

Обратная задача

Используя полученные координаты вершин треугольника, вычислить из решения обратной геодезической задачи длины и азимуты всех сторон треугольника и сравнить результаты.

Схема решения

Для вычислений предлагаем использовать компьютерную программу SFEGEO.EXE.

При ее запуске отобразиться меню:

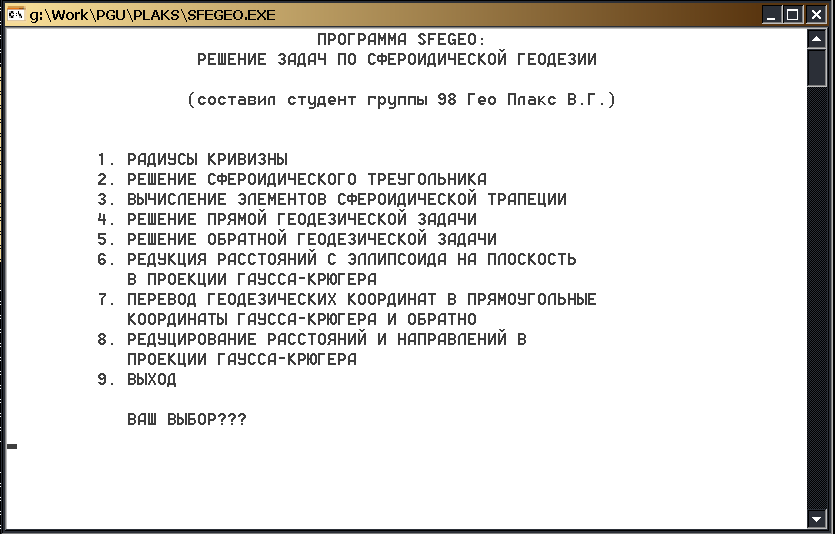
Для решения прямой геодезической задачи необходимо ввести с клавиатуры цифру 4 и нажать клавишу ВВОД. В следующем подменю аналогичным образом выбирают пункт «РЕШЕНИЕ ПРЯМОЙ ГЕОДЕЗИЧЕСКОЙ ЗАДАЧИ ДЛЯ МАЛЫХ И СРЕДНИХ РАССТОЯНИЙ» (т.е. ввести цифру 1 и нажать клавишу ВВОД). После этого программа переходит в режим ввода координат начальной точки. Сначала вводят значение широты и нажимают клавишу ВВОД. Потом – значения долготы, азимута и расстояния, нажимая после каждого значения клавишу ВВОД.

Важно: Угловые величины (т.е. значения широты, долготы, азимута) должны вводится в следующем формате: ГММСС.долисекунд. Например значение 52°20'00.000'' вводят как 552000, а значение 65°12'34.567'' вводят как 651234.567

После того как введено значение расстояния и нажата клавиша ВВОД, программа решает прямую геодезическую задачу (вычисляет координаты конечной точки и обратный азимут) и выводит результат на экран.

Чтобы продолжить решать прямую геодезическую задачу для других точек, вводят с клавиатуры цифру 1 и нажимают клавишу ВВОД. Для завершения работы с модулем решения прямой геодезической задачи, вводят с клавиатуры цифру 2 и нажимают ВВОД:

-

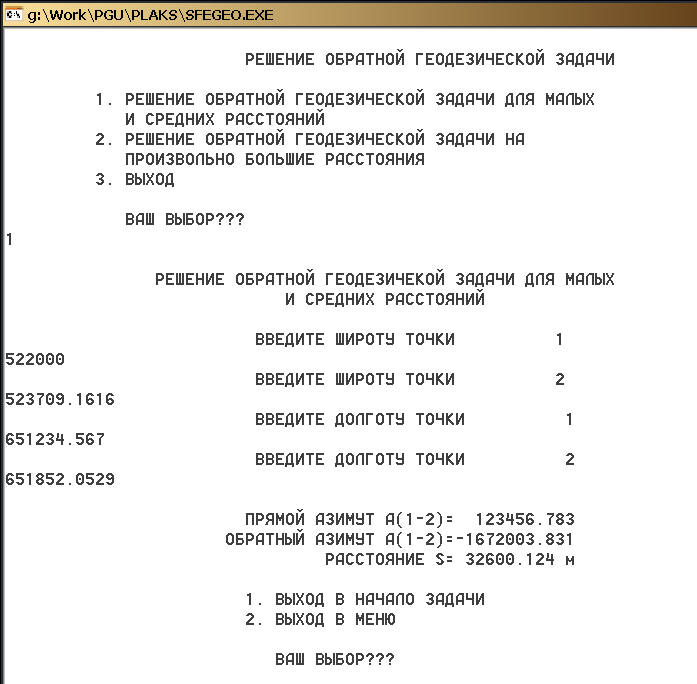
Для решения обратной геодезической задачи в главном меню выбирают пункт 5. В следующем подменю аналогичным образом выбирают пункт «РЕШЕНИЕ ОБРАТНОЙ ГЕОДЕЗИЧЕСКОЙ ЗАДАЧИ ДЛЯ МАЛЫХ И СРЕДНИХ РАССТОЯНИЙ» (т.е. вводят цифру 1 и нажимают клавишу ВВОД). После этого программа переходит в режим ввода координат начальной и конечной точки. После ввода каждого значения широты или долготы нажимают клавишу ВВОД. После того, как введены координаты обех точек, программа решает обратную геодезическую задачу и выводит результат на экран.

Чтобы продолжить решать обратную геодезическую задачу для других точек, вводят с клавиатуры цифру 1 и нажимают клавишу ВВОД. Для завершения работы с модулем решения обратной геодезической задачи, вводят с клавиатуры цифру 2 и нажимают ВВОД:

4. Решение задач проекции Гаусса – Крюгера

Дата добавления: 2014-11-06