Максимальное и минимальное касательное напряжение

Главное напряжение. Инварианты тензора напряжений. Эллипсоид напряжений

ГЛАВНЫЕ НАПРЯЖЕНИЯ. кРУГИ мОРА

Пусть задана система координат 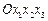и некоторая площадка dS с вектором нормали 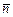. Будем считать, что в точке Р известен тензор напряжений 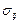(рис.3.1). Соотношение 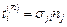ставит в соответствие каждому направлению 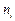вектор напряжения 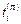. Направления, для которых вектора коллинеарны называются главными направлениями (или главными осями) тензора напряжений. Для главного направления имеет место равенство

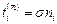, (3.1)

где скалярная величина s - это модуль вектора 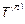которая называется главным напряжением. Подставляя (3.1) в 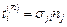и используя тождества 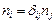и 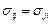, получим

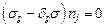, (i =1, 2, 3) (3.2)

или в тензорном виде

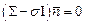, (3.2^¢)

где I – единичный тензор. Т.к. в (3.2) индекс i =1, 2, 3, то мы имеем систему трех однородных уравнений относительно 4-х неизвестных, а именно три направляющих косинуса n_j (j =1, 2, 3) и величину главного напряжения s.

Для того чтобы система (3.2) имела еще и нетривиальное решение, кроме n_j =0, детерминант из коэффициентов 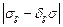должен обращаться в нуль, т.е.

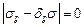или . (3.3)

Фактически, это есть задача о поиске собственных значений тензора (матрицы) S. Т.к. тензор напряжений является симметричным тензором, то уравнение (3.3) имеет три действительных корня.

Раскрывая определитель (3.3), получим кубическое уравнение

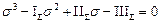, (3.4)

где 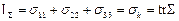- называется первым инвариантом тензора напряжений (trS - след S). Величина

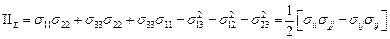- называется вторым инвариантом тензора напряжений. Соответственно - третий инвариант тензора напряжений.

Три корня уравнения (3.4) s₍₁₎, s₍₂₎, s₍₃₎ являются значениями трех главных напряжений. Каждому главному напряжению s_{( k )} соответствует главная ось, для которой направляющие косинусы 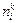находятся как решения уравнений

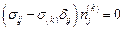(j =1, 2, 3) (3.5)

и равенства

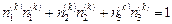, (3.6)

где k – это номер главного напряжения (собственного значения). Подставляя в (3.5) поочередно главные значения s₍₁₎, s₍₂₎, s₍₃₎ и решая каждую из трех полученных систем, получаем координаты направляющих косинусов 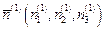, 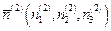и 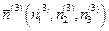, определяющих направление трех главных осей тензора напряжений. Все полученные площадки будут взаимно ортогональны, все три главных оси будут попарно ортогональны. Матрица тензора напряжений, отнесенная к главным осям, имеет следующий вид

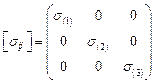или . (3.7)

Во второй формуле (3.7) в качестве индексов использованы римские цифры для того, чтобы показать, что главные напряжения (по договоренности) выбраны упорядоченными .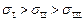

Если координатные оси направлены по главным осям, т.е. тензор напряжений имеет диагональный вид (3.7), то формулы для инвариантов тензора напряжений запишутся следующим образом:

,

,

.

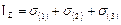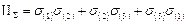Рассмотрим пространство главных напряжений, где оси координат совпадают с осями главных напряжений (рис.3.2). Произвольный вектор напряжения 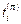вычисляется по формуле 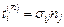. Т.к. для всех компонент тензора напряжений в главных осях при i ¹ j, 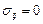, то компоненты вектора напряжений имеют вид:

, , .

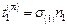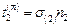Поскольку на направляющие косинусы накладывается условие 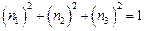, то вектор 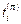в пространстве главных напряжений удовлетворяет уравнению

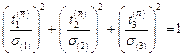, (3.8)

в чём легко убедиться, если выразить компоненты главной нормали через компоненты главных напряжений. Уравнение (3.8) называется уравнением эллипсоида напряжений Ламе.

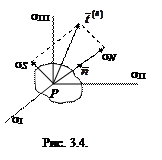
Рассмотрим систему координат, которая отнесена к главным осям. Разложим вектор напряжения 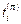на ортогональные компоненты – нормальную s _N и касательную s _S (рис.3.3). Величину нормальной компоненты можно определить по формуле

. (3.9)

Квадрат величины касательного напряжения имеет вид

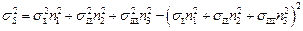(3.10)

Будем считать, что сами главные напряжения 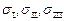известны. Тогда квадрат касательной компоненты напряжения будет зависеть от компонент вектора нормали n ₁, n ₂, n ₃, для которых выполняется условие n_i n_i =1. Максимальная компонента касательного напряжения действует в плоскости, которая делит пополам прямой угол между направлениями максимального и минимального главных напряжений находится по формуле

, .

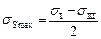Дата добавления: 2014-11-06