Производная неявной функции

Логарифмическая производная.

При нахождении производной от показательно-степенной функции , а также от громоздких выражений, допускающих логарифмирование, удобно применять логарифмическую производную. Логарифмической производной от функции 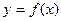называется производная от логарифма модуля этой функции:

.

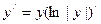Пример 1. Используя логарифмическую производную, найти производную функции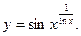

Решение. 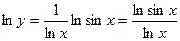. Продифференцируем обе части последнего равенства:

.

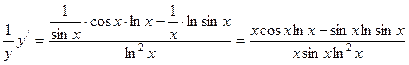Отсюда

.

Пример 2. Используя логарифмическую производную, найти производную функции

.

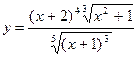Решение. Продифференцируем обе части последнего равенства:

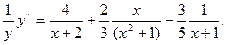
Отсюда

Пусть функция 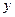задана неявно уравнением 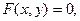и принимает в точке значение При некоторых условиях на функцию 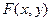(они будут обсуждаться во втором семестре) функция 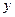будет дифференцируема. Ее производную можно найти, продифференцировав уравнение и разрешая полученное уравнение относительно .

Пример 1. Найти производную неявно заданной функции .

Решение. Продифференцировав обе части равенства, получаем

Тогда

Таким образом, 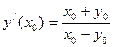(ответ зависит от того, какое значение функция принимает в точке ).

4) Теоремы о функциях, имеющих производную.

Теоремы настоящего параграфа являются основным средством, с помощью которого локальное, согласно определению, понятие производной оказывается эффективным орудием исследования свойств функции на отрезке.

Теорема 1 (Ферма). Пусть 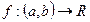принимает в точке наибольшее (наименьшее) значение и дифференцируема в точке . Тогда .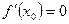

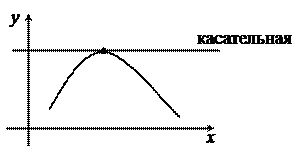Геометрическое толкование производной – производная есть тангенс угла наклона касательной. Обращение в нуль производной геометрически означает, что в точке касательная параллельна оси х.

Теорема 2 (Ролля о нуле производной). Пусть f непрерывна на отрезке , дифференцируема на интервале , и . Тогда такая, что .

Геометрический смысл теоремы Ролля: если в концах отрезка функция принимает равные значения, то на интервале найдется точка 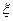, такая что касательная в 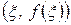параллельна оси х-ов.

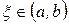Теорема 3. Если функция f (х) непрерывна на отрезке , дифференцируема на интервале , то найдется точка такая, что

. (1)

Формула (1) называется формулой Лагранжа или формулой конечных приращений.

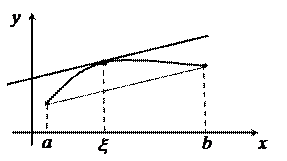Геометрический смысл теоремы: через точки , 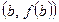проведем секущую. На интервале найдется точка x такая, что касательная в точке 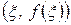параллельна секущей. Точку 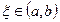можно записать в виде 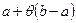при некотором .

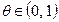Следствие 1. Пусть 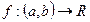дифференцируема на и 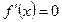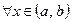. Тогд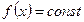а на .

Следствие 2. Пусть 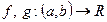дифференцируемы на и 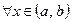. Тогда .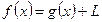

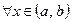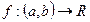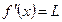
Следствие 3. Пусть дифференцируема на и постоянна на : 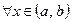. Тогда для некоторого

.

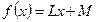
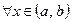Теорема 4. Если каждая из двух функций и непрерывна на отрезке , дифференцируема на интервале , и если 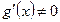для 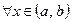, то найдется точка 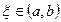такая, что

(2)

Формула (2) называется обобщенной формулой конечных приращений или формулой Коши.

5) Исследование монотонности функции с помощью производных.

Теорема 1. Пусть . Предположим, что Тогда 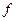неубывающая на

Теорема 2. Пусть 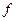определена и дифференцируема на 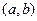. Для того, чтобы 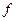возрастала на 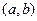, необходимо и достаточно, чтобы выполнились условия:

1)

2) не существует интервала

Пример 1. Согласно Теореме 2 функция возрастает на

Дата добавления: 2014-11-06