Методические рекомендации 3 страница

1₂ЕХ"" — ТХ" — К_х = 0,

(20,14)

ljEY"- — TY" — К_у = 0.

К выражениям (20,5) для перерезывающей силы надо прибавить теперь члены, равные проекциям действующей вдоль вектора t силы Т на оси хну:

F_x = —Е1₂Х"-'- + ТХ', Fy = —E/jY"-'- + TY'. (20,15)

Эти формулы могут быть, конечно, получены и непосредственно из (19,3).

Большая сила Т может в некоторых случаях появиться и в ре­зультате самого изгиба, даже если нет никаких специально при­ложенных растягивающих сил. Рассмотрим стержень, оба конца которого заделаны или закреплены на шарнирах в неподвижных опорах, так что не могут испытывать продольного смещения. Тогда прогиб стержня неизбежно сопровождается его удлине­нием, что и приводит к появлению в нем силы Т. Легко оценить величину прогиба, при котором эта сила делается существенной. Длина L + AL изогнутого стержня равна интегралу

L + AL = J /l+X'" + y'⁸dz,

о

взятому по прямой, соединяющей точки опоры. При слабом изгибе можно разложить корень в ряд, и мы получаем для удли­нения AL выражение

AL = -i-1 (Х'^г- + Y'²)dz. о

Возникающая при простом растяжении сила натяжения равна относительному удлинению, умноженному на модуль Юнга и на площадь 5 сечения стержня. Таким образом, сила Т равна

L

7 =-f£-J (X'² + ГV*. (20,16)

о

Если б есть порядок величины поперечного прогиба, то про­изводные X' и У — порядка б/L, так что весь интеграл, стоящий в (20,16), — порядка величины (6/L)² L = 6²/L и Т ~ ES (б//.)². Порядок величины первых и вторых членов в (20,14) — соответ­ственно IE6JL* и Тб/L⁸ <~ £S6³/L*. Момент инерции / имеет по­рядок величины / ~ A⁴, a S ~ Л², где h — толщина стержня". Подставляя это, легко получаем, что первые и вторые члены в (20,14) сравниваются по порядку величины при б ~ h.

Таким образом, при изгибе стержней, концы которых закреп­лены, можно пользоваться уравнениями равновесия в виде (20,4), только если прогиб мал по сравнению с толщиной стержня. Если же б не мало по сравнению с h (но, конечно, по-прежнему б < L), то надо пользоваться уравнениями {20,14). При этом сила Т в этих уравнениях заранее неизвестна. При их решении надо сначала рассматривать Т как заданный параметр, а затем по полученному решению определить Т согласно формуле (20,16), чем и определится связь Т с приложенными к стержню изгиба­ющими силами.

Обратным предельным случаем валяется тот, когда сопротив­ление стержня на изгиб мало по сравнению с его сопротивлением на растяжение, так что в уравнениях (20,14) можно пренебречь первыми членами по сравнению со вторыми. Физически такой случай может быть осуществлен либо очень сильным растяже­нием Т, либо при достаточно малом EJ, что может быть связано с мглой толщиной h (о сильно натянутых стержнях говорят как о струнах). Уравнения равновесия гласят в этих случаях:

ТХ" + К_х = 0, TY- + К_у = 0. (20,17)

Концы струны надо представлять себе закрепленными в том смысле, что их координаты заданы, т. е.

X = Y = 0. (20,18)

Направление же концов не может быть задано произвольным сбразом, а определяется решением уравнений.

В заключение покажем, каким образом уравнения равновесия слабо изогнутого стержня можно получить, исходя из вариацион­ного принципа, используя выражение (18,10) для упругой энер­гии:

F_c, = -^\\hYⁿⁱ + ^\dz.

В равновесии должна быть минимальна сумма этой энергии и потенциальной энергии, связанной с действующими на стержень внешними силами К, т. е. должно быть

bF_CT - J (К_х ЬХ + К_у bY) dz = 0

(второй член представляет собой работу внешних сил при беско­нечно малом смещении линии етержня). При варьировании F_CT производим дважды интегрирование по частям:

4- б JX"²dz== jX" ЬХ" dz=X" ЬХ' | - JX'" ЬХ' dz=

= X''bX'\~X'"bx\+\X""bXdz

и аналогичным образом для интеграла от Y"². Собирая различные члены, получим

JKEIjY""~ Ку)ЬУ + (EI_tX""- К_х)bX]dz+

+Eh (Y" bY' - Y" bY) I+£/₂(X"ЬХ'- Х'"ЬХ)| = 0.

Из первого, интегрального, члена следуют ввиду произвольности вариаций ЬХ и bY уравнения равновесия (20,4). Остальные же, проинтегрированные, члены дают граничные условия к этим уравнениям; так, на свободном конце вариации ЬХ, 67, ЬХ', bY'- произвольны и соответственно получаются условия (20,11). В то же время коэффициенты при ЬХ й 6У в этих членах дают выражения (20,5) для компонент перерезнвающей силы, а коэф­фициенты при йХ¹ и bY'- — выражения (20,3) для компонент изги­бающего момента.

Наконец, уравнения равновесия (20,14) при наличии растя­гивающей силы Т можно получить тем же способом, прибавив к варьируемой энергии величину

Т AL =4J-J(X'²+ Y'²)dz,

представляющую собой работу силы Т на пути AL — удлинении стержня.

Задачи

1. Определить форму прогиба стержня (длины /) под влиянием собствен­ного веса при различных способах закрепления его концов.

Решение. Искомая форма определяется решением уравнения

= qlEI

(q — вес единицы длины стержня) с теми или другими граничными условиями на его концах, сформулированными в тексте. При различных способах закрепле­ния концов стержня получаются следующие формы прогиба и максимальные смещения (так называемые стрелки прогиба); начало координат везде выбрано в одном из концов стержня.

а) Оба конца стержня заделаны:

384 El

t-Tfe-'f-o-. £(т)Ч

I \ _ 5 qt* 384 El

б) Оба конца оперты:

+с(4-)

в) Один конец (г = /)■ заделан, а другой (г = 0) оперт:

С = ТИ?7- ² (^2г3 - ^3iz* + ^/3)' С (0,42/) = 0,0054 -

48£/ ^{v 1} " tov.—/ _£/ •

г) Один конец (г = 0) заделан, а другой (г = /) свободен:

с—sir *<*-««+«">. ^s(,) = t-Ir-

2. Определить форму прогиба стержня под влиянием приложенной к его
середине сосредоточенной силы /.

Решение. Везде, кроме точки г = 1/2, имеем уравнение £,"" = 0, Гра-
ничные условия в концах стержня (г = 0 и г = /) определяются способом закре-
пления; в точке же г = 1/2 должны быть непрерывны £, а разность пере-
резывающих сил F — —Ell," по обе стороны этой точки должна быть равна
силе /.

Форма стержня (на участке 0 <: г ^ 1/2) и стрелка прогиба даются следу­ющими формулами.

а) Оба конца стержня заделаны:

е=«17-^г2<³'-^4г>> с(тЬтшт-

б) Оба конца стержня оперты:

^ = i8ir^z<^3ia-⁴²²b s(t)-w-

Форма стержня симметрична относительно его середины, так что функция £ (г) на участке 1/2^2^. / получается отсюда просто заменой г на / — г.

3. То же для стержня, один из концов которого (г = 0) заделан, а другой
(z=/) свободен, причем к последнему приложена сосредоточенная сила f.

Решение. Вдоль всего стержня F = const = /, так что £"' = — f/El, С условиями £ = 0, £ = 0 при г = 0 и £" = 0 при г = / получаем

£=-«4г*²(з/-2), ио=-^//3

6Е1 ^v " ^bv ' ЗЕ1 '

4. Определить форму прогиба стержня с закрепленными концами под влия нием сосредоточенной пары сил, приложенной к его середине.

Решение. Вдоль всей длины стержня £*" = 0, а в точке г = 1/2 момент М = £7£" испытывает скачок, равный моменту m приложенной сосредоточен­ной пары. С соответствующими условиями на концах получим:

а) Оба конца стержня заделаны:

1 = -~_тг*(1-2г) при 0<2<//2,

24Е11

б) Оба конца закреплены в шарнирах: т

■ г (i^a — Щ при 0 < г < 1/2,

^--шп^{-¹~^г){1г-^А{1-^г)'^{] при 1}'²<¹<^и

По обе стороны от точки г = 1/2 стержень изогнут в разные стороны.

5. То же, если сосредоточенная пара приложена к свободному концу стерж-
ня, другой конец которого заделан.

Решение. Вдоль всей длины стержня имеем М = Eli" = m, а в точке г = 0: £ = 0, £' = 0. Форма изгиба дается формулой

^fc 2Е1 ^г '

6. Определить форму стержня (кругового сечения) с закрепленными в шар-
нирах концами, растягиваемого силой т и изгибаемого силой /, приложенной
к его середине.

Решение» На отрезке 0 ^ г ^ 1/2 перерезывающая сила равна //2, так что (20,15) дает уравнение

т f

I"-------- —- £' г- '

El ^fc 2EI '

Граничные условия: £ = 0, {' = 0 при г = 0,1, а при t= U2 должно быть £' = 0 (в силу непрерывности £'). Для формы стержня (на отрезке 0 ^ г ^ 1/2) полу­чим формулу

^E-'^Wz •

При малых й это выражение переходит в формулу, полученную в задаче 2, б. При больших же значениях k оно переходит в

£ = -|jjt-z,

т. е., в согласии с уравнением (20.17), гибкая нить принимает под влиянием силы / форму, составленную из двух прямых отрезков, пересекающихся в точ­ке 2 = 112.

Если сила Т сама возникает в результате растяжения стержня поперечной силой, то для ее определения надо воспользоваться формулой (20,16). Подста­вив в нее полученное выражение, найдем уравнение

8ЕЧ*

1 Г 3. 1... Ы 3,. kl I

f [ 2 ^т 2 2 kl 2 j" PS '

определяющее в неявном виде т как функцию от /,

7. Стержень (кругового сечения) бесконечной длины лежит на упругом основании, т. е. при изгибе на него действует сила /С = —а£, пропорциональная црогибу. Определить форму, принимаемую стержнем-при действии на него со­средоточенной силы f.

Решение. Выбираем начало координат в точке приложения силы /, Везде, кроме точки г = 0, имеет место уравнение

Е1\г = -а£.

выражение для перерезывающей силы

и выражение для изгибающего момента

а*

EI

М-

(С + Г)

(ср. конец § 20), Постоянная а определяется условием отсутствия общего растя" жения стержня.

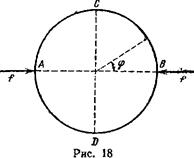
9. Определить деформацию кругового кольца, изгибаемого двумя сосредо­точенными силами /, действующими вдоль диаметра (рис. 18).

Решение. Интегрируя уравнение (1) по всей длине кольца, найдем, что

2jkwj= JК_га Лр = 2/.

Везде, кроме точек <р = 0 и ф = я, имеем уравнение (i) с К_г — 0:

Г" + 2Г + С + _^7-=0.

Искомая деформация кольца симмет­рична относительно диаметров АВ и CD, в силу чего в точках А, В, С, D должно быть £'=0. Разность значений перерезывающей силы при <р-+±0 должна быть равна /. Удовлетворяющее этим условиям решение уравнения равнове­сия есть

/а³ /1,1 я 1. \ „ ^ ^

£ = -£7" [j? + -4-<pcos<p — -д-соэф—^-sin, 0<ф<я.

В частности, точки Л и В взаимно сближаются на величину

§21. Устойчивость упругих систем

Поведение стержня, подверженного воздействию продольных сжимающих сил, представляет простейший пример важного явления упругой неустойчивости, впервые обнаруженного Л. Эйлером.

При отсутствии поперечных изгибающих внешних сил К_х, K_v уравнения равновесия сжатого стержня (20,14) имеют очевидное решение X = Y — 0, соответствующее стержню, остающемуся при воздействии продольной силы Т прямолинейным. Это решение, однако, соответствует устойчивому равновесию стержня лишь до тех пор, пока сжимающая сила \Т\ остается меньше некоторого критического значения Т_кр. При | "7" 1 < Т_кр прямо­линейная форма стержня устойчива по отношению к произволь­ному малому возмущению. Другими словами, если под влиянием какого-либо малого воздействия стержень подвергается слабому изгибу, то по прекращении этого воздействия стержень будет стремиться вернуться в исходное состояние.

Напротив, при | Т | > Г_кр прямолинейная форма отвечает неустойчивому равновесию. Достаточно уже бесконечно малого воздействия (изгиба) для того, чтобы равновесие нарушилось, в результате чего произойдет сильный изгиб стержня. Ясно, что в этих условиях сжатый стержень вообще не сможет реально существовать в неизогнутом виде.

Поведение стержня после потери им устойчивости должно описываться уравнениями сильного изгиба. Однако самое значе­ние критической нагрузки Т_нр может быть получено с помощью уравнений слабого изгиба. При | Т\ = Гщ, прямолинейная форма стержня соответствует некоторому безразличному равновесию. Это, значит, что наряду с решением X = Y — 0 должны суще­ствовать еще и состояния слабого изгиба, которые тоже являются равновесными. Поэтому критическое значение Т_кр можно опре­делить как то" значение |Т|, при котором у уравнений

Е1_гХ'-'-^и + \Т\Х" = 0. f/jV"" + | Т | У^! = 0 (21,1)

появляется отличное от нуля решение. Само же это решение определяет характер деформации, которой подвергнется стержень непосредственно после потери им устойчивости.'

В задачах этого параграфа приведен ряд типичных случаев потери устойчивости различными упругими системами.

Задачи

1. Определить критическую сжимающую силу для стержня с шарнирно
закрепленными концами.

Решение. Поскольку нас интересует наименьшее значение |7"|, при котором появляется отличное от нуля решение уравнений (21,1), то достаточно рассмотреть лишь то из этих двух уравнений, которое содержит меньшее из hi hi пусть /₂ < h- Ищем решение уравнения

Е1₂Х"'^! + \ Т\Х"= 0

в виде

Х= А+ Вг+ Csinfa+Dcosfe, k= (| 7 |/£7₂) *^/з.

Отличное от нуля решение, удовлетворяющее условиям X — 0, X" = 0 при г — 0 и 2 = /, есть

X = С sin kz,

причем должно быть sin kl = 0. Отсюда находим искомую критическую силу

Г_кр = я²£7₂//².

После потери устойчивости стержень примет форму, изображенную на рис. 19, а,

2. То же для стержня с заделанными концами (рис. 19, б).
Решение. Г_кр = 4п²£/₂//².

3. То же для стержня, один из концов которого заделан, а другой свободен
(рис. 19, в).

Решение. Т_кр = я²£/₂/4/².

4. Определить критическую сжимающую силу для стержвя (кругового се­чения) с шарнирно закрепленными концами, лежащего на упругом основании (см. задачу 7 § 20).

Решение. Вместо уравнений (21,1) здесь надо рассмвтреть уравнение

■■ Л sin

ия ~т~

Е1Х""- + | Т | X"- + аХ = 0. Аналогичное исследование приводит к решению

я²£/ /„. а/<

п²я⁴£/

причем для п должно быть взято то из целых значений, для коНэрого получается наименьшее значение Т_Кр. При достаточно больших значениях а получается и > 1, т. е. после потери устойчивости стержень принимает форму с несколь­кими пучностями.

5. Стержень кругового сечения подверг­нут кручению, и его концы заделаны. Опре­делить критическую величину кручения, после которой прямолинейная форма стер­жня делается неустойчивой.

а)

Решение. Критическое значение угла кручения определяется появлением отличных от нуля решений уравнений сла­бого изгиба закрученного стержня. Для вы­вода этих уравнений подставляем выраже­ние (19,7):

М = £7

+ Cit

(т — постоянный угол кручения) в уравнение (19,3); это дает

El

^Ст"Ш—^{[Ft] = 0}-

Дифференцируем это уравнение; поскольку изгиб слабый, то при дифференци­ровании первого и третьего членов можно считать t постоянным, равным век­тору t₀, направленному по оси стержня (оси г). Помня также, что dF/dl = 0 (внешние силы по длине стержня отсутствуют), получаем

£/[t₀4i]+CT-^-=0,

или в компонентах:

ух __хх^я = 0, X"" + нУ = 0,

где х = Ст/£/. Введя в качестве неизвестной функцию | = X -J^ iY, получим уравнение

6«- йсБ" = о.

Ищем решение, удовлетворяющее условиям % = 0, |' = 0 при г = 0, I в виде Б = а(1 +гх2 — е^Ы2) + Ьг\

и находим в качестве условия совместности для получающихся для а и b урав­нений соотношение

%1 2

Наименьший корень этого уравнения: и//2 = 4,49, так что

8,98£/ ^ткр ^_ С1 '

6. То же для стержня с шарнирно закрепленными концами.
Решение Здесь получается

причем х определяется из е*^к' = 1, т. е. xl = 2я. Поэтому искомый критиче­ский угол кручейия

т_кр = 2лЕ1/С1.

7. Определить предел устойчивости вертикального стержня, находящегося
под действием собственного веса; нижний конец стержня заделан.

Решение. Если продольное натяжение f_z = т меняется вдоль длины

стержня, то в первом члене в, (20,1) ^ ф 0 и вместо уравнений (20,14) по­лучается

/₂£Х"«— (тх')' — к_х = 0, l_xey"-" _ (jy'y _ к._у = 0.

В данном случае поперечные изгибающие силы отсутствуют по всей длине стержня, а т = —q (i — Z), где q — вес единицы длины стержня, a z отсчиты-вается от его нижнего конца. Предполагая, что /₂<3 h, рассматриваем урав­нение

1_гех^п=тх'=—q(l—z)x'

(при z - / автоматически имеем x" = 0). Общий интеграл этого уравнения для функции и = x' есть

где

Граничные условия x' = 0 при г = 0 и x" = 0 при г = i дают для функции и (т)) условия

2 / аР \1/2, „

и = 0 при Ч = % =-g-^-gT^)» и'т)'» = 0 при tj = 0.

Для того чтобы удовлетворить этим условиям, надо положить 6 = 0, причем ■'-i/,("По) ⁼ °^- Наименьший корень этого уравнения г\₀ = 1,87, откуда находим критическую длину стержня

4,_.._И (-f-f.

8. Стержень обладает вытянутой формой поперечного сечения, так что
/»~> h. Один конец стержня заделан, а к свободному концу приложена сила /,
изгибающая его в главной плоскости х, z (в которой жесткость на изгиб есть
Е1₂). Определить критическое значение /_кр, после которого плоская форма из-
гиба становится неустойчивой и стержень отгибается в боковую сторону (в пло-
скости у, г), одновременно испытывая кручение.

Решение. Ввиду большой величины жесткости Е1₂ по сравнению с Eli (и с жесткостью на кручение С)¹) неустойчивость по отношению к" сильному боковому изгибу возникает в то время, когда изгиб в плоскости х, z остается еще слабым. Для определения момента наступления неустойчивости надо соста­вить уравнения слабого бокового изгиба стержня, сохраняя в них члены, про­порциональные произведениям действующей в плоскости х, г_;-силы / на малые смещения. Поскольку сосредоточенная сила приложена лифь к свободному концу стержня, то вдоль всей его длины F = f, а на свободном конце (z = /) момент М = 0; по формуле (19,6) находим компоненты момента относительно закрепленной системы координат х, у, г;

М_я = 0, M_y = (l-z)f, M_Z=(Y-Y_u)f,

где Y_B = Y (/). Проецируем эти моменты на связанные в каждой точке со стерж­нем оси координат |, т|, £; с точностью до членов первого порядка по смещениям получим

Mg = <p(i-z)/, Мт, = — г)/,

Л*_£ = (/-г)/-^- + /(7-К₀),

где ф — полный угол поворота сечения стержня^при его за*ручивании (угол кручения т = dq>/dz здесь не постоянен вдоль длины стержня). С другой стороны, согласно (18,6) и (18,9) имеем при слабом изгибе

Mi = — EIJ", М_л = Е1_гХ", Mi = Сф'

и, сравнивая эти выражения, получим уравнения равновесия

EJ₂X" = (l-z)f,

EhY" = -ф (I - z) f, С_Ф' = (I - z) fY' -f- (У — У„) /.

Первое из этих уравнений определяет основной изгиб стержня в плоско­сти х, г; требуется иайти значение /, при котором появляется отличное от нуля решение у второго и третьего уравнений. Исключая из них Y, найдем

_ф" + k²(l — z)²<p = 0, k² = p/EIiC Общий интеграл этого уравнения есть

_Ф = a VT=z J_1/t (А (/ - г)*) + b V~z J__1/t (/ - z)*).

*) Так, для узкого прямоугольного сечения с шириной А и высотой b > А имеем

На заделанном конце (z = 0) должно быть ф = 0, а на свободном крутящий момент Сф' = 0. Из второго условия имеем а = 0, а первое дает J__lj,_i(kl²/2) — 0. Наименьший корень этого уравнения: kP/2 = 2,006, откуда

ГЛАВА III

УПРУГИЕ волны

§ 22, Упругие волны в изотропной среде

Если в деформируемом теле происходит движение, то темпера­тура тела, вообще говоря, отнюдь не постоянна, а меняется как со временем, щк и от точки к точке вдоль тела. Это обстоятельство сильно усложняет точные уравнения движения в общем случае произвольных движений.

Обычно, однако, положение упрощается благодаря тому, что передача тепла из одного участка тела в другой (посредством про­стой теплопроводности) происходит очень медленно. Если тепло­обмен практически не происходит в течение промежутков времени порядка периода колебательных движений в теле, то можно рас­сматривать каждый участок тела как теплоизолированный, т. е. движение будет адиабатическим. Но при адиабатических деформа­циях a_lk выражается через и_ш по формулам обычного вида с той лишь разницей, что вместо обычных (изотермических) значений величин Е, а надо брать их адиабатические значения (см. § 6). Ниже мы будем считать это условие выполненным, и соответст­венно этому под Е и а в этой главе будут подразумеваться их адиабатические значения.

Для того чтобы получить уравнения движения упругой среды, надо приравнять силу внутренних напряжений da_thldx_h произ­ведению ускорения u_t на массу единицы объема тела, т. е. на его плотность р:

p**=ilr- (ад

¹) Подразумевается, что скорость v точек среды совпадает с производной и от ее смещения. Подчеркнем, однако, что отождествление этих двух величин отнюдь не является чем-то само собой разумеющимся. В кристаллах вектор и представляет собой смещение узлов решетки; скорость же v определяется в ме­ханике сплошных сред как импульс единицы массы вещества. Равенство v = и справедливо, строго говоря, лишь для идеальных кристаллов, где в каждом узле решетки (и только в них) находится по атому. Если же кристалл содержит дефекты (незаполненные.узлы — вакансии, или же, напротив, лишние атомы в междоузлиях), то перенос массы относительно решетки (т. е. отличный от нуля импульс) может существовать и в недеформированной решетке — за счет диффузии дефектов «сквозь решетку». Отождествление v и и подразумевает прене­брежение этими эффектами — в связи с медленностью диффузии или малой концентрацией дефектов.

Это — общий вид уравнений движения ^г).

В частности, уравнения движения изотропной упругой среды можно написать непосредственно по аналогии о уравнением рав­новесия (7,2). Имеем

Р" = ТТГТ^)- ^AU + 2(1+0)^(1-20 S^{rad diV} (²²'²)

Поскольку все деформации предполагаются малыми, то рас­сматриваемые в теории упругости движения представляют собой малые упруеие колебания или волны. Начнем с рассмотрения пло­ской упругой волны в неограниченной изотропной среде, т. е. волны, в которой деформация и является функцией только от одной из координат, скажем, от х (и qt времени). B<ie производные по у и z в уравнениях (22,2) исчезают, и мы получаем для отдель­ных компонент вектора и следующие уравнения:

д²и_х 1 д*и_х _ _n dbiy _____ 1 d²"gf _ _n „.

дх* ~ с\ di* ' ^Uj дх* cj dt* £~ ^и ^ ' >

(уравнение для u_z такое же, как для и_у), где введены обозна­чения ¹):

°^{l =} [р(1 + а)(1-2о) ] ' ' °^t= Up Да) ] ' * ⁽²²'⁴⁾

Уравнения (22,3) представляют собой обычные волновые урав­нения в одном измерении, и входящие в них величины с_г и c_t являются скоростями распространения волны. Мы видим, что скорость распространения волны оказывается различной для компоненты и_х, с одной стороны, и компонент щ, и_г — с другой.

Таким образом, упругая волна представляет собой по суще­ству две независимо распространяющиеся волны. В одной из них (и_х) смещение направлено вдоль распространения самой волны; такую волну называют продольной, она распространяется со ско­ростью Ci. В другой (и_у, u_z) — смещение направлено в плоскости, перпендикулярной направлению распространения; такую волну называют поперечной, она распространяется со скоростью c_t. Как видно из (22,4), скорость с_г всегда больше скорости c_t ²):

_Ci>(4/3)V2_C<. (22,5)

¹) Дадим также выражения скоростей ci и С(через коэффициенты сжатия и сдвига и через коэффициенты Ламэ: / ЗК + 4ц. у/2 /Я + 2ц, у/2 /МЛ¹/^{2 а}) При фактическом изменении о в пределах от 0 до 1/2 (см. примечание на стр. 26) имеет место и более сильное неравенство ц > cj j^2,

Скорости с_г и Ct называют продольной и поперечной скоростями звука.

Мы знаем, что изменение объема при деформации определяется суммой диагон&&йъ1Х членов тензора деформации, т. е. величиной Hjj = div и. В поперечной волне имеются только компоненты u_v, щ, и поскольку они не зависят ни от у, ни от г, для такой волны div и = 0. Таким образом, поперечные волны не связаны с избие­нием объема отдельных участков тела. Напротив, для продольных волн div и Ф 0; эти волны сопровождаются сжатиями и расши­рениями в теле.

Разделение волны на две независимо распространяющиеся с разными скоростями части можно произвести и в общем случае произвольной (не плоской) упругой волны в неограниченном про­странстве.

Перепишем уравнение (22,2), введя в него скорости e_t и c_t'
и = с? Ли + (с²-cf) grad div и. (22,6)

Представим вектор а в виде суммы двух частей:

и = щ + щ, (22,7)

из которых одна удовлетворяет условию

div щ = 0, (22,8)

а другая — условию

rot щ = 0. (22,9)

Из векторного анализа известно, что такое представление всегда возможно (это есть представление вектора в виде суммы ротора некоторого вектора и градиента некоторого скаляра). При подстановке и = щ + щ в (22,6) получаем

, и/ +»ь = с\ Д (и, + и,) + (с| - с|) grad div и,. (22,10)

Применим к обеим сторонам этого уравнения операцию div. Поскольку div u₍ == 0, мы получим

div щ = ct Д div ti/ -j- (cf — с?) Д div u,,

или

div {щ — с] Smi) = 0.

С другой стороны, rot стоящего в скобках выражения тоже равен нулю в силу (22,9). Но если rot и div некоторого вектора исче­зают во всем пространстве, то этот вектор тождественно равен нулю. Таким образом,

*£--с?Ди, = 0. (22,11)

Аналогично применяя к уравнению (22,10) операцию rot и помня, что rot Uj = 0 и что rot всякого градиента равен нулю, находим

rot(tb — с) Ди*) — 0.

Поскольку div стоящего в скобках выражения тоже равна нулю, то мы приходим опять к уравнению того же вида^как и (22,11);

Дата добавления: 2014-11-06