
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Умови та розв’язки по усіх класах
|
|
|
|
Орієнтовні завдання для районів м. Києва
II етап Всеукраїнської учнівської олімпіади з математики 2011/12 н. р.
6 клас
1. Який із двох виразів більший:
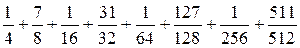 чи
чи  ?
?
Відповідь: перший вираз більший.
Розв’язання. Підрахувати, який із виразів більший, можна безпосередньо, звівши обидва до спільного знаменника. А можна зробити інакше — згрупувати доданки у другому виразі в пари:
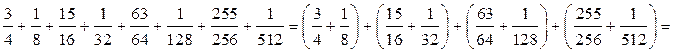
Оскільки перший вираз складається із тих самих чотирьох доданків, але крім них містить іще й чотири інших доданки, він є більшим за другий вираз.
2. Знайдіть найменше чотирицифрове число, яке ділиться на 9 і всі цифри якого різні.
Відповідь: 1026.
Розв’язання. Число 1026, усі цифри якого різні, ділиться на 9, бо сума його цифр ділиться на 9. Є лише два менших чотирицифрових числа, що кратні 9: 1017 і 1008. Але перше з них містить дві одиниці, а друге — два нулі. Отже, найменшим числом, що задовольняє умову, є 1026.
3. У кожній клітині таблиці  записане число 0 або 1. Леся порахувала суми чисел у кожному рядку. Якщо записати ці суми в порядку зростання, вийде набір 0, 1, 2, 2, 2, 5, 6 та 8. Андрійко ж підрахував суми чисел у кожному стовпчику. Якщо записати в порядку зростання його суми, вийде набір 0, 2, 2, 3, 4, 4, 5 та 6. Чи не помилився хтось із діток у своїх підрахунках?
записане число 0 або 1. Леся порахувала суми чисел у кожному рядку. Якщо записати ці суми в порядку зростання, вийде набір 0, 1, 2, 2, 2, 5, 6 та 8. Андрійко ж підрахував суми чисел у кожному стовпчику. Якщо записати в порядку зростання його суми, вийде набір 0, 2, 2, 3, 4, 4, 5 та 6. Чи не помилився хтось із діток у своїх підрахунках?
Відповідь: хтось мав помилитися.
 Розв’язання. Якби Леся правильно підрахувала всі суми, у таблиці був би рядок, сума чисел якого дорівнює 8. Такий рядок має складатися лише з одиниць, тобто не може містити жодного нуля. Але тоді у кожному стовпчику була би принаймні одна одиниця, і стовпчика із сумою 0 бути не могло б. А це означало би, що помилився Андрій. Отже, або Леся, або Андрій помилилися.
Розв’язання. Якби Леся правильно підрахувала всі суми, у таблиці був би рядок, сума чисел якого дорівнює 8. Такий рядок має складатися лише з одиниць, тобто не може містити жодного нуля. Але тоді у кожному стовпчику була би принаймні одна одиниця, і стовпчика із сумою 0 бути не могло б. А це означало би, що помилився Андрій. Отже, або Леся, або Андрій помилилися.
|
|
|
4. Усередині квадрата зі стороною 6 розмістили п’ять однакових прямокутників, як це показано на рис. 1 (сторони прямокутників паралельні до сторін квадрата). Знайдіть площу одного такого прямокутника.
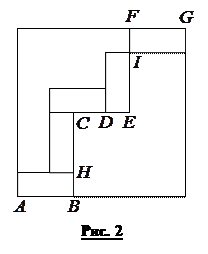 Відповідь: 2.
Відповідь: 2.
Розв’язання. Нехай менша сторона прямокутника дорівнює a, а більша сторона дорівнює b. Розглядаючи горизонтальні сторони прямокутників (рис. 2), одержимо таку рівність:
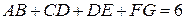 , тобто
, тобто  ,
,
звідки 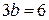 , отже
, отже  .
.
Аналогічно, розглядаючи вертикальні сторони прямокутників, матимемо:
 , тобто
, тобто 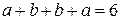 ,
,
звідки 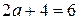 , отже
, отже 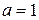 .
.
Значить, площа прямокутника дорівнює 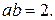
7 клас
1. Який із двох виразів більший:
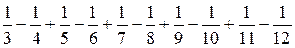 чи
чи  ?
?
Відповідь: перший вираз більший.
Розв’язання. Підрахувати, який із виразів більший, можна безпосередньо, звівши обидва до спільного знаменника. А можна зробити інакше — згрупувати доданки та від’ємники в пари:
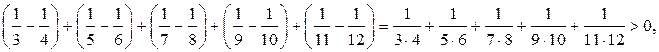

Оскільки перший вираз додатний, а другий — від’ємний, перший вираз є більшим.
2. Знайдіть найменше п’ятицифрове число, яке ділиться на 9 і всі цифри якого різні.
Відповідь: 10 269.
Розв’язання. Число буде найменшим, якщо якомога меншими є його перші цифри, зокрема якщо перша цифра числа — 1, а друга цифра — 0. За умовою цифри числа не мають повторюватися, тож найменше можливе значення третьої цифри — 2. Для того, щоб число було кратним 9, треба, щоб сума двох його останніх цифр та цифр 1, 0 і 2 була кратною 9, тобто дорівнювала 9 чи 18. Це означає, що сума двох останніх цифр числа повинна дорівнювати 6 або 15. У першому випадку двома останніми цифрами можуть бути 06, 15, 24, 33, 42, 51 або 60; жодна з цих пар не дасть разом із цифрами 102 число, всі цифри якого різні. Якщо ж сума двох останніх цифр — 15, це або 69, або 78, або 87, або 96. Пара цифр 69 і дає найменше число, що задовольняє умову: 10 269.
3. Чи можна розфарбувати всі 12 частин рис. 3 у три кольори так, щоб жодні дві частини, пофарбовані однаково, не мали спільної межі?

Відповідь: не можна.
|
|
|
Розв’язання. Спробуємо розфарбувати рисунок у червоний, зелений та синій кольори. Центральний круг можна зафарбувати у довільний із трьох кольорів. Пофарбуймо його червоним. Усі 11 секторів мають спільну межу із центральним кругом, а отже жоден із них фарбувати у червоний колір після цього не можна.
Розглянемо перший сектор. Його слід фарбувати або в зелений, або в синій колір. Пофарбуймо його зеленим. Тоді другий сектор не може бути ні зеленим, ні червоним, тобто маємо зробити його синім. Тепер третій сектор не може бути синім і не може бути червоним, отже фарбуємо його зеленим і т. д. Вийде так, що 11-й сектор ми пофарбуємо зеленим кольором. Але тоді сусідні 1-й та 11-й сектори матимуть однакові кольори. Отже, розфарбувати рисунок потрібним чином не вдасться.
4. Сторони чотирикутника ABCD мають такі довжини:  ,
,  ,
, 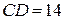 ,
,  . Знайдіть довжину діагоналі AC, якщо відомо, що вона є цілим числом.
. Знайдіть довжину діагоналі AC, якщо відомо, що вона є цілим числом.
Відповідь: 
Розв’язання. Застосуймо нерівність трикутника до  та до
та до  : для першого матимемо, що
: для першого матимемо, що  , тобто що
, тобто що 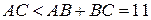 , а для другого трикутника — що
, а для другого трикутника — що 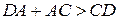 , тобто
, тобто 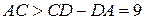 . Таким чином,
. Таким чином,  , звідки
, звідки 
Зауважимо, що чотирикутник, описаний в умові задачі, нескладно сконструювати. З допомогою тригонометрії можна показати, що він є опуклим.
5. Леся написала на дошці кілька попарно різних натуральних чисел. Андрійко не зміг вибрати серед цих чисел трьох, сума яких ділилася б на 3. Яку найбільшу кількість чисел могла виписати Леся?
Відповідь: 4 числа.
Розв’язання. Леся могла написати на дошці, приміром, такі чотири числа: 3, 4, 6, 7. Те, що сума жодних трьох із них не ділиться на 3, легко перевірити безпосереднім перебором.
Припустімо тепер, що Лесі вдалося виписати набір із п’яти чисел, який задовольняє умову. Розглянемо остачі, що їх дають записані числа в разі ділення на 3. Є лише три можливі залишки від ділення на 3 — 0, 1 і 2. Якщо всі три трапляються серед п’яти остач, які ми розглядаємо, то сума відповідних трьох чисел даватиме при діленні на 3 остачу 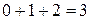 , тобто ділитиметься на 3. А якщо одного із залишків 0, 1, 2 немає, то за принципом Діріхле деяка з інших двох остач траплятиметься серед наших п’яти залишків хоча б тричі. Але й у цьому випадку сума трьох відповідних чисел ділитиметься на 3. Суперечність.
, тобто ділитиметься на 3. А якщо одного із залишків 0, 1, 2 немає, то за принципом Діріхле деяка з інших двох остач траплятиметься серед наших п’яти залишків хоча б тричі. Але й у цьому випадку сума трьох відповідних чисел ділитиметься на 3. Суперечність.
|
|
|
Отже, найбільша кількість чисел, які могла написати на дошці Леся, — 4.
8 клас
1. Обчисліть значення виразу:
 .
.
Відповідь: 4 044 119.
Розв’язання. Проведімо такі перетворення:
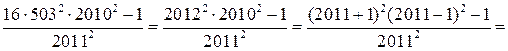

2. Чи існують цілі числа x, y, z, які задовольняють рівність:
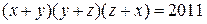 ?
?
Відповідь: таких чисел не існує.
Розв’язання. Якби такі три числа x, y та z існували, принаймні два з них мали би однакову парність. Припустимо, це пара чисел x та y. Тоді сума 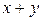 — парна, а отже парним мав би бути й добуток
— парна, а отже парним мав би бути й добуток  . Число ж 2011, якому цей добуток повинен дорівнювати, — непарне. Одержана суперечність показує, що цілих чисел, які задовольняють умову, не існує.
. Число ж 2011, якому цей добуток повинен дорівнювати, — непарне. Одержана суперечність показує, що цілих чисел, які задовольняють умову, не існує.
3. У першій коробці кілька жовтих кульок, а у другій — кілька блакитних. Андрій перекладає декілька кульок із першої коробки в другу, після чого перемішує вміст другої коробки. Далі Леся перекладає таку ж саму кількість кульок із другої коробки в першу. Яких кульок тепер більше: жовтих у другій коробці чи блакитних у першій?
Відповідь: їх однакова кількість.
Розв’язання. Нехай діти перекладали з коробки в коробку по n кульок, причому серед n кульок, які переклала Леся, жовтих було m, а блакитних —  . Тоді жовтих кульок у другій коробці після Андрієвого перекладання було n, а після Лесиного стало
. Тоді жовтих кульок у другій коробці після Андрієвого перекладання було n, а після Лесиного стало  . Блакитних же кульок у першій коробці після Андрієвого перекладання не було взагалі, а після Лесиного стало
. Блакитних же кульок у першій коробці після Андрієвого перекладання не було взагалі, а після Лесиного стало  — стільки ж, скільки й жовтих кульок у другій коробці.
— стільки ж, скільки й жовтих кульок у другій коробці.
4. Знайдіть усі такі прості числа p та q, для яких число  також є простим.
також є простим.
Відповідь: 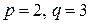 або
або 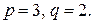
Розв’язання. Якщо числа p та q непарні, то число  парне і, очевидно, більше за 2, а тому не може бути простим. Отже, серед простих чисел p та q є парне, яке дорівнює 2. Припустимо, що таким є число p. Лишається знайти всі прості q, для яких простим є число
парне і, очевидно, більше за 2, а тому не може бути простим. Отже, серед простих чисел p та q є парне, яке дорівнює 2. Припустимо, що таким є число p. Лишається знайти всі прості q, для яких простим є число 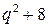 .
.
Помітимо, що коли число не ділиться на 3, себто дає при діленні на 3 остачу 1 або 2, квадрат цього числа дає від ділення на 3 остачу 1, а тому якщо 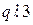 , то
, то 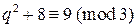 , тобто число
, тобто число  ділиться на 3 і не є простим. Таким чином,
ділиться на 3 і не є простим. Таким чином,  , звідки
, звідки  . Аналогічно, якщо
. Аналогічно, якщо 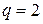 , то
, то  . Залишається підставити пари (2, 3) і (3, 2) у початковий вираз і пересвідчитися, що обидві справді дають просте число 17.
. Залишається підставити пари (2, 3) і (3, 2) у початковий вираз і пересвідчитися, що обидві справді дають просте число 17.
|
|
|

5. A й B — точки перетину кіл 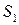 та
та  таких, що центр кола
таких, що центр кола 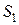 лежить на колі
лежить на колі  , а центр кола
, а центр кола  лежить на колі
лежить на колі 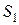 . Точку C, відмінну від точки B, вибрано на колі
. Точку C, відмінну від точки B, вибрано на колі 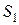 так, що
так, що  . Знайдіть кути трикутника ABC.
. Знайдіть кути трикутника ABC.
Відповідь: усі кути дорівнюють по 
Розв’язання. Позначмо центри кіл 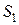 та
та  як
як 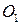 і
і 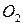 відповідно (рис. 4). Оскільки за умовою
відповідно (рис. 4). Оскільки за умовою  і
і 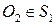 ,
,  — спільний радіус цих кіл, і, зокрема, кола мають однакові радіуси. Тож маємо такі рівності:
— спільний радіус цих кіл, і, зокрема, кола мають однакові радіуси. Тож маємо такі рівності:
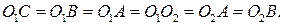
Звідси трикутники  та
та  рівносторонні, а
рівносторонні, а 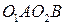 — ромб із гострим кутом
— ромб із гострим кутом 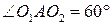 . Тому
. Тому 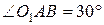 . Далі,
. Далі, 
 за трьома сторонами, звідки
за трьома сторонами, звідки 

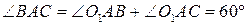 . А оскільки трикутник ABC рівнобедрений, решта його кутів теж рівні
. А оскільки трикутник ABC рівнобедрений, решта його кутів теж рівні 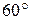 .
.
9 клас
1. За яких значень параметра a рівняння

має рівно два різних дійсних корені?
Відповідь: 

Розв’язання. Число x буде коренем рівняння тоді й лише тоді, коли 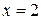 або ж
або ж 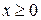 і
і  (а якщо так, то
(а якщо так, то 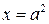 ). Тобто для того, щоб рівняння мало два різних корені, необхідно і достатньо, щоб існувало таке
). Тобто для того, щоб рівняння мало два різних корені, необхідно і достатньо, щоб існувало таке  , що
, що  . Це справджується для всіх
. Це справджується для всіх 
2. Від’ємні числа a, b, c, d задовольняють такі умови:  ,
,  ,
,  . Яке число більше: a чи c?
. Яке число більше: a чи c?
Відповідь: 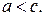
Розв’язання. Виразимо b із кожного з трьох рівнянь:
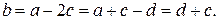
Тоді 

 , а також
, а також 

 . Оскільки всі числа від’ємні,
. Оскільки всі числа від’ємні,  .
.
Зауважимо, що набір чисел, які задовольняють умову, існує: приміром, 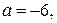

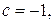

3. На дошці записано числа 1, 2, 3,..., 101. Андрійко може вибрати серед записаних чисел довільні два a, b та записати замість них число 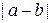 . Після 100-ї такої операції на дошці залишиться єдине число. Яке найбільше значення воно може мати?
. Після 100-ї такої операції на дошці залишиться єдине число. Яке найбільше значення воно може мати?
Відповідь: 101.
Розв’язання. Оскільки всі числа на дошці залишатимуться невід’ємними на кожному кроці, а для невід’ємних чисел a та b завжди  , можемо стверджувати, що числа́, більшого за 101, на дошці опинитися на може. Число 101, з іншого боку, справді може залишитись останнім. Для цього Андрійку достатньо зробити так: спершу провести операції з парами чисел (1, 2), (3, 4), …, (99, 100) — записати замість кожної з цих пар одиницю. Далі він розіб’є отримані 50 одиниць на 25 пар і проведе операції з ними, внаслідок чого дістане 25 нулів, записаних на дошці разом із числом 101, яке Андрійко не чіпав. Далі хлопець по одному прибиратиме нулі, ставлячи їх у пари із числом 101.
, можемо стверджувати, що числа́, більшого за 101, на дошці опинитися на може. Число 101, з іншого боку, справді може залишитись останнім. Для цього Андрійку достатньо зробити так: спершу провести операції з парами чисел (1, 2), (3, 4), …, (99, 100) — записати замість кожної з цих пар одиницю. Далі він розіб’є отримані 50 одиниць на 25 пар і проведе операції з ними, внаслідок чого дістане 25 нулів, записаних на дошці разом із числом 101, яке Андрійко не чіпав. Далі хлопець по одному прибиратиме нулі, ставлячи їх у пари із числом 101.
Отже, найбільшим числом, яке може лишитися після 100 операцій, є число 101.
4. Знайдіть усі натуральні значення n, для яких обидва числа 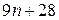 та
та  є точними квадратами.
є точними квадратами.
Відповідь: 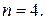
Розв’язання. Нехай деяке число n задовольняє умови задачі, причому 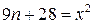 та
та 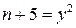 , де x та y — цілі і, без втрати загальності, додатні числа. Тоді маємо:
, де x та y — цілі і, без втрати загальності, додатні числа. Тоді маємо:

Оскільки 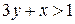 , а 17 — просте число, повинна справджуватися система:
, а 17 — просте число, повинна справджуватися система:

Звідси відразу знаходимо, що 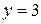 , а
, а 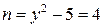 . Перевіркою переконуємось, що значення
. Перевіркою переконуємось, що значення 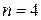 задовольняє умову задачі.
задовольняє умову задачі.
 5. У трикутнику ABC проведено бісектрису BD. Відомо, що центр описаного навколо
5. У трикутнику ABC проведено бісектрису BD. Відомо, що центр описаного навколо  кола збігається із центром кола, що вписане у
кола збігається із центром кола, що вписане у 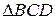 . Знайдіть кути
. Знайдіть кути  .
.
Відповідь: 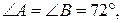

Розв’язання. Позначмо спільний центр кіл через I, а точки дотику вписаного у 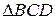 кола до сторін CD, BC і BD через E, F, G відповідно (рис. 5). Відрізки IE та IF — серединні перпендикуляри до сторін AC й BC відповідно, а тому
кола до сторін CD, BC і BD через E, F, G відповідно (рис. 5). Відрізки IE та IF — серединні перпендикуляри до сторін AC й BC відповідно, а тому  та
та 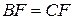 . Із властивостей дотичних до кола
. Із властивостей дотичних до кола  ,
, 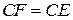 і
і 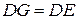 , тому
, тому

Також маємо, що
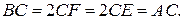
Отже, трикутники BDC та ACB рівнобедрені. Звідси маємо, що
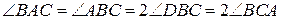



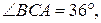

10 клас
1. За яких значень параметра a рівняння

має рівно три різних дійсних корені?
Відповідь: 
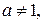

Розв’язання. Рівняння можна переписати як  , тому число x буде коренем цього рівняння тоді й лише тоді, коли
, тому число x буде коренем цього рівняння тоді й лише тоді, коли  ,
, 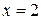 або
або  — тобто
— тобто 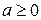 і
і 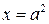 . Таким чином, рівняння матиме три різні корені тоді й тільки тоді, коли
. Таким чином, рівняння матиме три різні корені тоді й тільки тоді, коли 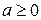 , причому
, причому 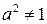 і
і  , тобто
, тобто 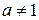 і
і 
2. Нескінченна спадна геометрична прогресія має перший член m, знаменник 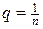 , а сума її членів дорівнює 3. Знайдіть усі можливі пари
, а сума її членів дорівнює 3. Знайдіть усі можливі пари  за умови, що m та n — натуральні числа.
за умови, що m та n — натуральні числа.
Відповідь: 
Розв’язання. Оскільки сума членів геометричної прогресії, описаної в умові задачі, дорівнює  , нам необхідно знайти всі натуральні m та n
, нам необхідно знайти всі натуральні m та n 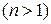 такі, що
такі, що 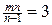 . Можемо записати:
. Можемо записати:
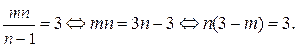
Звідси, оскільки n — натуральне і не дорівнює 1, 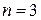 , а
, а 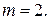
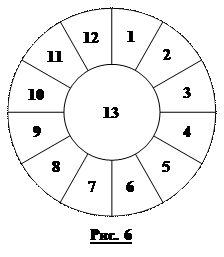
3. У скільки способів можна розфарбувати всі 13 частин рис. 6 у три кольори так, щоб жодні дві частини, пофарбовані однаково, не мали спільної межі? Два розфарбування вважаються різними, якщо хоча б одна з 13 частин пофарбована по-різному.
Відповідь: 6.
Розв’язання. Центральну частину можна пофарбувати в один із трьох кольорів. Тоді всі 12 секторів доведеться фарбувати в інші два кольори, адже кожен із секторів має спільну межу із центральною частиною. Сектор 1 можна пофарбувати у довільний із двох кольорів, а кольори решти секторів встановлюються після цього автоматично: сектор 2 має бути пофарбовано в колір, відмінний від кольору центральної частини і сектора 1; сектор 3 повинен бути пофарбований у колір, відмінний від кольору центральної частини й сектора 2 і т. д. Легко бачити, що таке розфарбування справді задовольнятиме умову задачі, адже пара секторів 12 і 1 також буде розфарбована по-різному.
Отже, маємо 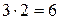 варіантів розфарбування.
варіантів розфарбування.
4. Доведіть, що для будь-яких дійсних чисел 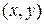 справджується нерівність:
справджується нерівність:

Розв’язання. Щоб довести нерівність, можна розглянути випадки: всі можливі комбінації знаків виразів 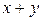 ,
, 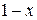 та
та  . Утім, можна зробити простіше — скористатися нерівністю
. Утім, можна зробити простіше — скористатися нерівністю  , яка справджується для довільного дійсного числа a:
, яка справджується для довільного дійсного числа a:

 5. У чотирикутнику ABCD, що вписаний у коло, діагональ AC є бісектрисою кута DAB. На промені AD за точкою D вибрано точку E. Доведіть, що
5. У чотирикутнику ABCD, що вписаний у коло, діагональ AC є бісектрисою кута DAB. На промені AD за точкою D вибрано точку E. Доведіть, що  тоді й тільки тоді, коли
тоді й тільки тоді, коли 
Розв’язання. AC — бісектриса, тому, як відомо,  (рис. 7). Крім того,
(рис. 7). Крім того,  .
.
Якщо  , то
, то  (за двома сторонами та кутом між ними), звідки
(за двома сторонами та кутом між ними), звідки 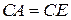 .
.
Навпаки, якщо 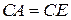 , то
, то 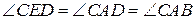 , звідки
, звідки  (за рівними кутами та парою сторін
(за рівними кутами та парою сторін 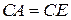 )
) 

11 клас
1. Знайдіть усі значення  , що задовольняють рівняння:
, що задовольняють рівняння:

Відповідь: 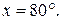
Розв’язання. Зі співвідношення

дістаємо рівність 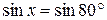 , з якої, враховуючи, що
, з якої, враховуючи, що  , маємо, що
, маємо, що 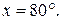
2. Позначимо через P (n) та S (n) відповідно добуток та суму цифр натурального числа n. Наприклад, 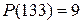 ,
, 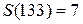 . Знайдіть усі двоцифрові числа n, для яких справджується рівність:
. Знайдіть усі двоцифрові числа n, для яких справджується рівність: 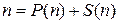 .
.
Відповідь: 19, 29, 39, 49, 59, 69, 79, 89, 99.
Розв’язання. Нехай шукане двоцифрове число 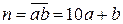 ,
,  . Рівняння з умови набуває такого вигляду:
. Рівняння з умови набуває такого вигляду:

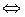


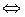
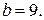
Отже, умову задовольняють усі двоцифрові числа, що закінчуються на 9, і лише вони.
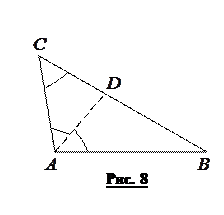 3. У трикутнику ABC відрізок AD — бісектриса
3. У трикутнику ABC відрізок AD — бісектриса 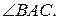 Виявилося, що
Виявилося, що 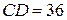 ,
,  , а
, а 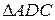 — рівнобедрений з вершиною D. Знайдіть довжини сторін
— рівнобедрений з вершиною D. Знайдіть довжини сторін 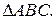
Відповідь: 
Розв’язання. Зрозуміло, що  (рис. 8). Із рівності кутів
(рис. 8). Із рівності кутів 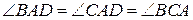 випливає, що
випливає, що 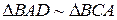 , що дає співвідношення:
, що дає співвідношення:
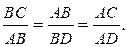
Звідси  ,
, 
Зауважимо, що трикутник зі сторонами 
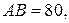
 справді задовольняє умову задачі: бісектриса AD ділить сторону BC у відношенні
справді задовольняє умову задачі: бісектриса AD ділить сторону BC у відношенні  і дорівнює, після застосування теореми косинусів до трикутників ACB й ACD, 36.
і дорівнює, після застосування теореми косинусів до трикутників ACB й ACD, 36.
4. У кожній клітинці квадратної таблиці 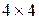 міститься число 0 або число 1. Поряд із таблицею записали 10 чисел: суми значень у кожному з 4 рядків, суми значень у кожному з 4 стовпчиків і суми чисел на кожній із 2 великих діагоналей (тих діагоналей, що містять по чотири клітинки). Доведіть, що серед одержаних десяти чисел є принаймні три однакових.
міститься число 0 або число 1. Поряд із таблицею записали 10 чисел: суми значень у кожному з 4 рядків, суми значень у кожному з 4 стовпчиків і суми чисел на кожній із 2 великих діагоналей (тих діагоналей, що містять по чотири клітинки). Доведіть, що серед одержаних десяти чисел є принаймні три однакових.
Розв’язання. У кожному рядку, стовпчику та на кожній діагоналі містяться чотири числа, кожне з яких дорівнює 0 або 1, тому кожна записана сума може бути одним із п’яти чисел: 0, 1, 2, 3, 4. Якби серед 10 сум не було трьох однакових, це означало би, що кожне з п’яти можливих значень трапляється серед сум рівно двічі. Нехай це справді так. Розгляньмо одну з двох ліній, сума чисел на якій дорівнює 4; така лінія складається виключно з одиниць. Це не може бути діагональ, адже тоді в кожному рядку й у кожному стовпчику містилася би принаймні одна одиниця, тобто кількість ліній із сумою 0 була б меншою за дві. Хай тоді, без втрати загальності, лінія із сумою 4 — рядок. Це означає, що в кожному стовпчику й на кожній діагоналі є принаймні одна одиниця. Тоді дві лінії із сумою чисел 0 — теж рядки. Але в такому випадку друга лінія із сумою 4 теж не може бути ані стовпчиком, ані діагоналлю, тобто є рядком. Отже, маємо по два рядки із сумами 0 та 4, що означає, що сума чисел у кожному з чотирьох стовпчиків дорівнює 2, а це суперечить припущенню, що кожне значення від 0 до 4 трапляється серед сум рівно двічі. Одержана суперечність і завершує доведення.
5. Функція  задовольняє такі умови:
задовольняє такі умови:
o 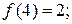
o 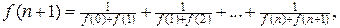
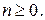
Знайдіть значення 
Відповідь: 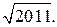
Розв’язання. Для довільного 
 , звідки
, звідки 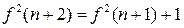 . Використавши умову
. Використавши умову 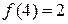 , матимемо:
, матимемо:
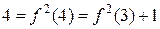

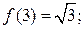


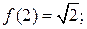



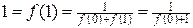

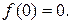
Із допомогою методу математичної індукції покажемо, що 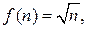
 . Базу індукції доведено вище. Індукційний перехід здійснимо, скориставшись співвідношенням
. Базу індукції доведено вище. Індукційний перехід здійснимо, скориставшись співвідношенням 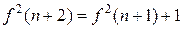 :
:
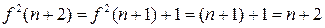


Неважко індукцією показати й те, що функція 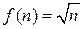 справді задовольняє умову задачі: якщо
справді задовольняє умову задачі: якщо  , то
, то
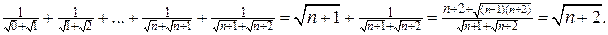
Отже, 
|
|
|
|
Дата добавления: 2014-11-07; Просмотров: 2731; Нарушение авторских прав?; Мы поможем в написании вашей работы!