Сложение одинаково направленных колебаний. Биения

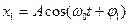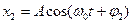Рассмотрим колебания одного направления и одной частоты: (1) и (2).

Для нахождения уравнения результирующего колебания воспользуемся методом векторных диаграмм. На чем основан этот метод? Из точки О на оси Х под углом φ, равным начальной фазе откладывается вектор длины А.

Колебания, описываемые с помощью уравнений (1) и (2) представим с помощью векторов и 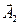(см. рисунок). Построим по правилу сложения векторов результирующий вектор 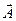. Проекция этого вектора на ось Х равна сумме проекций складываемых векторов 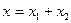. Вектор 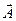представляет собой результирующее колебание.

(3).

Таким образом, уравнение результирующего колебания: ,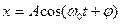

где А и φ удовлетворяют уравнениям (3).

Мы получили, что векторная диаграмма дала возможность свести сложение нескольких колебаний к операции сложения векторов. Этот прием очень полезен в оптике, где световые колебания в некоторой точке определяются как результат наложения многих колебаний, приходящих в данную точку от различных участков волнового фронта.

Формулы (3) можно получить, сложив выражения (1) и (2) и произведя соответствующие преобразования с помощью тригонометрических функций. Однако метод векторных диаграмм обладает большой наглядностью и простотой.

Проанализируем формулу (3) для амплитуды:

1) Если разность фаз 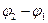=0, то 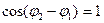и амплитуда результирующего колебания: .

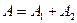2) Если разность фаз 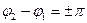, то и амплитуда результирующего колебания: .

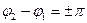٭(, то колебания находятся в противофазе)

Если частоты колебаний х ₁ и х ₂ неодинаковы, то и 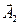будут вращаться с различными угловыми скоростями. В этом случае результирующий вектор 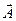пульсирует по величине и вращается с непостоянной скоростью. Результирующим движением в этом случае будет негармоническое колебание, а некоторый сложный колебательный процесс.

Особый интерес при этом представляет случай, когда два складываемых колебания одинаково направлены и мало отличаются по частоте. В результате сложения этих колебаний получается колебание с периодически меняющейся амплитудой. Колебания такого вида называют биениями.

Получим уравнение результирующего колебания. Пусть частота одного колебания , другого и начальные фазы равны нулю, а амплитуды колебаний одинаковы 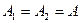. Тогда уравнения колебаний будут иметь вид:

и .

Складывая эти выражения и применяя тригонометрическую формулу преобразования (если уравнения записаны через 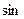, то ), получаем

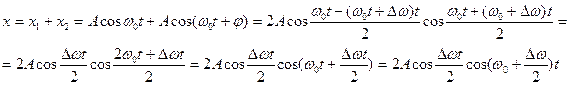
В этом выражении 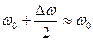, так как 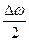мало по сравнению с .

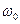Тогда 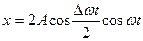(4). Характер этой зависимости покажем на рисунке. Результирующее колебание можно представить, как гармоническое колебание с частотой , амплитудой 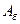, изменяющейся по периодическому закону: 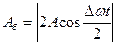. Частота изменения 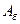в 2 раза больше частоты изменения косинуса (т.к. 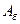берется по модулю), т.е. частота биений равна разности частот складываемых колебаний.

Дата добавления: 2014-11-07