Ol — V2X 47 страница

так что о² = е²р'²/р² и выражение (65,10) обращается в нуль, т. е. среднее изменение давления является эффектом более вы­сокого порядка, чем второй. Изменение же плотности

— 1 / <Э²р \ ТТ

в нуль не обращается¹). В этом же приближении имеем для среднего значения тензора плотности импульса в бегущей пло­ской (в указанном выше смысле) волне:

р' + PViV_k = р' + pQVtVb.

') Отметим, что производная (б^р/др²), фактически всегда отрицательна л поэтому в бегущей волне р' < 0*.

Первый член равен нулю, а во втором вводим единичный вектор л в направлении распространения волны (совпадающем с точ-

звук

!гл. vat

ностью до знака с направлением v). Воспользовавшись соотно­шением (65,2), будем иметь для плотности потока импульса:

й_1к=*Ёп,п„. (65,12>

Если волна распространяется вдоль оси х, то отлична от нуля только компонента Ш* = Е. Таким образом, в рассматриваемом приближении имеется средний поток только.«-компоненты им­пульса, причем он переносится в направлении оси х.

По поводу всего сказанного в последнем абзаце лишний pas подчеркнем, что речь идет о волновом цуге, ограниченном по своему сечению. Для волны, плоской в строгом смысле этого слова, эти результаты были бы несправедливы (в частности р' могло бы быть отличным от нуля уже в квадратичном прибли­жении— см. задачу 4 в § 101). Формально это связано с тем» что для строго плоской волны (которую нельзя обойти «сбоку») несправедливо, вообще говоря, утверждение о конечности потен­циала ip во веем пространстве (или в течение всего времени). Физическое различие связано с возможностью (в случае ограни­ченного по сечению волнового цуга) возникновения поперечного движения, приводящего к выравниванию среднего давления.

§ 66. Отражение и преломление звуковых волн

Когда звуковая волна падает на границу раздела между дву­мя различными средами, она отражается и преломляется. Дви­жение в первой среде является тогда наложением двух волн (па­дающей и отраженной), а во второй среде имеется одна (пре­ломленная) волна. Связь между всеми тремя волнами опреде­ляется граничными условиями на поверхности раздела.

Рассмотрим отражение и преломление монохроматической продольной волны в случае плоской границы раздела. Плоскость. уг выберем в качестве граничной. Легко видеть, что все три волны — падающая, отраженная и преломленная — будут иметь одинаковые частоты со и одинаковые компоненты k_y, k_z волно­вого вектора (но не компоненту k_x по направлению, перпенди­кулярному к плоскости раздела). Действительно, в неограни­ченной однородной среде монохроматическая волна с посто­янными к и со является решением уравнений движения. При наличии границы раздела добавляются лишь граничные условия,, которые в нашем случае относятся к * = 0, т. е. не зависят ни от времени, ни от координат у и г. Поэтому зависимость реше­ния от t и от у, г остается неизменной во всем пространстве и времени, т. е. со, k_y, k_z остаются теми же, какими они были в па­дающей волне.

Из этого результата могут быть непосредственно выведены соотношения, определяющие направления распространения от­раженной и преломленной волн. Пусть ху— плоскость падения волны. Тогда в падающей волне k_z = 0; то же самое должно иметь место и для отраженной и преломленной волн. Таким об­разом, направления распространения падающей, отраженной и преломленной волн лежат в одной плоскости.

Пусть 8 — угол между направлением волны и осью х. Тогда из равенства величин k_y = (и/с) sin 6 для падающей и отражен­ной волн следует, что

е,=е[, (66,1)

(66,2)

т. е. угол падения 9i равен углу отражения 8{. Из аналогичного же равенства для падающей и преломленной волн следует соот­ношение

sin 9i с₁

Sin 0₂ С_г

между углом падения 8i и углом преломления 0₂ (ci и с₂ — ско­рости звука в обеих средах).

Для того чтобы получить количественное соотношение между интенсивностями падающей, отраженной и преломленной волн, лишем потенциалы скорости в этих волнах соответственно в виде

Ф! = А1 ехр {ш> cos 8(+ -Jp sin 8₍ —,

_Ф; = A\ ехр {ш> (- ± cos 8, + -JL sin в, -1)],

Ф₂ = Л₂ехр {«о cos 8₂ + sin в₂ — /)}.

На поверхности раздела (* = 0) должны быть равными давле­ния (р = —рф) и нормальные скорости (v_x = д<р/дх) в обеих средах; эти условия приводят к равенствам

Коэффициент отражения R определяется как отношение средних (по времени) плотностей потока энергии в отраженной и падаю­щей волнах. Поскольку плотность потока энергии в плоской волне равна сро*, то имеем:

Простое вычисление приводит к результату

„_ f P2tge₂-p,tg8i у,_Rfi п

Углы 8i и 82 связаны друг с другом соотношением (66,2); выра­зив 8₂ через 8ь можно представить коэффициент отражения; в виде

Г р₂с₂ cos e_t - р, - с\ sin² 9, I
R = --------------------------- ЛГ—г '1'»- " (°М>

L Р₂С₂ COS 6[ + p_t *\J Cj — с₂ sin 6, J

Для нормального падения (8i = 0) эта формула дает просто»

\ р₂с₂ + PlCl)^v ' '

-При угле падения, определяющемся из

tg² e_t = f;₂~^p'₂;, (бб,е>

коэффициент отражения обращается в нуль, т. е. звуковая вол­на целиком преломляется, не отражаясь вовсе; такой случай, возможен, если Ci>c₂, но р₂с₂ > piCi (или наоборот).

Задача

Определить давление, оказываемое звуковой волной на границу раздела-между двумя жидкостями.

Решение. Сумма полных потоков энергии в отраженной и преломлен­ной волнах должна быть равна падающему потоку энергии. Относя поток энергии к единице площади поверхности раздела, напишем это условие в виде

cos 6j = c_lE_l cos 9! -f- c₂E₂ cos 6₂,

где £(, E[, E₂ — плотности энергии в падающей, отраженной и преломлен­ной волнах. Вводя коэффициент отражения R = EjE_l, имеем отсюда

С\ cos 01 с₂ cos 0₂

(1 -R) Ei.

Искомое давление р определяется как ^-компонента импульса, теряемого в; единицу времени звуковой волной (отнесенная к единице площади гранит* раздела). С помощью выражения (65,12) для тензора плотности потока им­пульса в звуковой волне найдем:

р = E_i cos² 0j + Е\ cos² 8, — Е₂ cos² 0^ Подставляя выражение для £₂, вводя R и используя (66,2), получим: p=ll Sin 0, COS0! [(1 +R) Ctg0! - (I — У?) ctg 6₂].

Для нормального падения (0₍ = 0) найдем с помощью (66,5)

2 2, 2 2 „_ „ 2 •

Р Г P|Cl + P2C2-2PlP2tl 1 ' L (Р,С, + Р2С₂)². J'

§ 67. Геометрическая акустика

Плоская волна отличается тем свойством, что направление ее распространения и ее амплитуда одинаковы во всем простран­стве. Произвольные звуковые волны этим свойством, конечно, не обладают. Однако возможны случаи, когда звуковую волну, не являющуюся плоской, в каждом небольшом участке простран­ства можно рассматривать как плоскую. Для этого необходимо, чтобы амплитуда и направление волны почти не менялись на протяжении расстояний порядка длины волны.

Если выполнено это условие, то можно ввести понятие о лучах как о линиях, касательные к которым в каждой точке со­впадают с направлением распространения волны, и можно гово­рить о распространении звука вдоль лучей, отвлекаясь при этом от его волновой природы. Изучение законов распространения звука в таких случаях составляет предмет геометрической аку­стики. Можно сказать, что геометрическая акустика соответ­ствует предельному случаю малых длин волн, л.->0.

Выведем основное уравнение геометрической акустики — уравнение, определяющее направление лучей. Напишем потен­циал скорости волны в виде

Ф = ае^г*. (67,1)

В случае, когда волна не плоская, но геометрическая акустика применима, амплитуда а является медленно меняющейся функ­цией координат и времени, а фаза волны тр есть «почти линей­ная» функция (напомним, что в плоской волне = kr — of 4-а с постоянными к и со). В малых участках пространства и малых интервалах времени фазу гр можно разложить в ряд; с точ­ностью до членов первого порядка имеем:

¹1> = + г grad ip + ^ /.

Соответственно тому, что в каждом небольшом участке про­странства (и в небольших интервалах времени) волну можно рассматривать как плоскую, определяем волновой вектор и ча­стоту волны в каждой точке как

k—fj—grad*, «—(67,2) Величина * называется эйконалом.

2/2 2 2 2 2

В звуковой волне имеем со /с =& = k_x + k_y + k_z. Подстав­ляя сюда (67,2), получим следующее основное уравнение гео­метрической акустики:

Если жидкость неоднородна, то коэффициент с² является функ­цией координат.

Как известно из механики, движение материальных частиц может быть определено с помощью уравнения Гамильтона-Яко-би, являющегося, как и уравнение (67,3), уравнением в частных производных первого порядка. Аналогичной \р величиной являет­ся при этом действие 5 частицы, а производные от действия определяют импульс р и функцию Гамильтона Н (энергию)' частицы согласно формулам р = dS/dr, Н = —dS/dt, ана­логично формулам (67,2). Известно, далее, что уравнение Га-мильтона-Якоби эквивалентно уравнениям Гамильтона, имею­щим вид р = —дН/дг, v = г = дН/др. Вследствие указанной аналогии между механикой материальной частицы и геометри­ческой акустикой мы можем непосредственно написать анало­гичные уравнения для лучей:

к=-^г, г = _ж. (67,4)

В однородной изотропной среде со = ck с постоянным с, так что k = 0, г = сп (п — единичный вектор в направлении к), т. е. как и должно было быть, лучи распространяются по прямым линиям, сохраняя при этом постоянную частоту со.

Частота остается, разумеется, постоянной вдоль лучей вообще всегда, когда распространение звука происходит в стационарных условиях, т. е. свойства среды в каждой точке пространства не меняются со временем. Действительно, полная производная от частоты по времени, определяющая ее изменение вдоль рас­пространяющегося луча, равна

d(0 За>, дт ■. <9ш

~аТ~"дГ^"дТ^Г^"Ш^к'

При подстановке (67,4) два последних члена взаимно сокра­щаются; в стационарном же случае da/dt = 0, а потому и da/dt = 0.

При стационарном распространении звука в неподвижной не­однородной среде со = ck, где с есть заданная функция коорди­нат. Уравнения (67,4) дают

г = сл, k = — kVc. (67,5)

Абсолютная величина вектора к меняется вдоль луча просто по закону k = со/с (с со = const). Для определения же изменения

направления п полагаем во втором из уравнений (67,5) k =-у п

и пишем:

-f-n-f n(Vcr) = -*Vc,

§ 67]

геометрическая акустика

откуда

dn dt

= — Vc + n (nVc).

Вводя элемент проходимой лучом длины dl = с dt, перепишем это уравнение в виде

dn Vc, п, „ _ч

(67,6)

которое и определяет распределение Е в пространстве.

Вторая из формул (67,4) определяет скорость распростране­ния волн по известной зависимости частоты от компонент вол­нового вектора. Это — важная формула, относящаяся не только к звуковым, но и ко всяким волнам вообще (мы уже пользова­лись, например, этой формулой в § 12 в применении к гравита­ционным волнам). Приведем здесь еще один вывод этой фор­мулы, полезный для уяснения смысла определяемой ею ско­рости. Рассмотрим волну (или, как говорят, волновой пакет), занимающую некоторую конечную область пространства. Пред­положим, что волна такова, что в ее спектральное разложение входят монохроматические компоненты с частотами, лежащими в некотором малом интервале; то же самое относится и к ком­понентам их волновых векторов. Пусть to есть некоторая сред­няя частота волны и к — средний волновой вектор. Тогда

Луч изгибается в сторону уменьшения скорости звука.

') Как известно из дифференциальной геометрии, производная dajdl вдоль луча равна N/Я, где N — единичный вектор главной нормали, a. R — радиус кривизны луча. Выражение же в правой стороне уравнения (67,6) есть, с точностью до множителя 1/с, производная от скорости звука по на­правлению главной нормали; поэтому можно написать это уравнение в виде

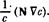
в некоторый начальный момент времени волна описывается функцией вида

Ф = е"<^г/(г). (67,8)

Функция Дг) заметно отлична от нуля только в некоторой ма­лой (но большой по сравнению с длиной волны \Jk) области пространства. Ее разложение в интеграл Фурье содержит со­гласно сделанным предположениям компоненты вида е'^гДк, где Ак — малые величины.

Таким образом, каждая из монохроматических компонент волны пропорциональна в начальный момент времени множи­телю вида

Ф_к = const е'(к+дк)г_ (₆₇₎₉)

Соответствующая ей частота есть ©(k-f-Ak) (напоминаем, что частота является функцией волнового вектора). Поэтому в мо­мент времени t та же компонента будет иметь вид

Фк = const • ехр {/ (к + Ак) г — т (к + Ак) t). Воспользовавшись малостью Ак, напишем:

со(к + Дк)~©(к) + 4£-Дк.

Тогда ф_К принимает вид

Ф_к = const е¹ ""-•»*> ехр {г Дк (г — /)}. (67,10)

Если теперь произвести обратное суммирование всех моно­хроматических компонент волны со всеми имеющимися в ней. Ак, то, как видно из сравнения (67,9) и (67,10), мы получим:

ф^еМкг-^г _(67Д1)

где / — та же функция, что и в (67,8). Сравнение с (67,8) пока­зывает, что за время t вся картина распределения амплитуды

в волне передвинулась в пространстве на расстояние — t (экс­поненциальный множитель перед f в (67,11) влияет только на фазу волны). Следовательно, скорость ее равна

и=!г- <⁶⁷'¹²>

Эта формула и определяет скорость распространения волны с произвольной зависимостью © от к. В случае © = ck с постоян­ным с она приводит, конечно, к обычному результату U = = ©/£ —с. В общем же случае произвольной зависимости ©(к) скорость распространения волны является функцией ее частоты и ее направление может не совпадать с направлением волнового вектора.

Скорость (67,12) называют также групповой скоростью вол­ны, а отношение a/k — фазовой скоростью. Подчеркнем, однако, что фазовая скорость не соответствует реальному физическому распространению чего бы то ни было.

По поводу изложенного вывода отметим, что выражаемое формулой (67,11) передвижение волнового пакета без измене­ния его формы является приближенным и связано с предполо­женной малостью интервала Дк. Вообще же говоря, при зави­сящей от © скорости U волновой пакет по мере своего распро­странения «размазывается» — занимаемая им в пространстве область расширяется. Можно показать, что это размазывание пропорционально квадрату величины интервала Дк волновых векторов, входящих в разложение волнового пакета.

Задача

Определить изменение с высотой амплитуды звука, распространяющегося в поле тяжести в изотермической атмосфере.

Решение. Вдоль изотермической атмосферы (рассматриваемой как идеальный газ) скорость звука постоянна. Плотность потока энергии, очевид­но, падает вдоль луча обратно пропорционально квадрату расстояния г от источника:

"2 ¹

сро^г со

Отсюда следует, что амплитуда колебаний скорости в звуковой волне ме­няется вдоль луча обратно пропорционально г -у'р. При этом плотность р меняется, согласно барометрической формуле, как

р сэ ехр (— ngz/RT) (?—высота, ц. — молекулярный вес газа, R — газовая постоянная).

§ 68. Распространение звука в движущейся среде

Соотношение w — ck между частотой и волновым вектором имеет место только для монохроматической звуковой волны, распространяющейся в неподвижной среде. Нетрудно получить аналогичное соотношение для волны, распространяющейся в движущейся среде (и наблюдаемой в неподвижной системе ко­ординат).

Рассмотрим однородный поток жидкости со скоростью и. На­зовем неподвижную систему координат х, у,? системой К и вве­дем также систему К' координат х', у', z', движущуюся относи­тельно системы К со скоростью и. В системе К' жидкость неподвижна, и монохроматическая волна в ней имеет обыч­ный вид:

р = Const в¹ <кг'-*с<).

Радиус-вектор г' в системе К' связан с радиусом-вектором г в си­стеме К равенством r' = r — ut. Поэтому в неподвижной системе координат волна имеет вид

Ф =' const е'^1кг- <**+*■»>'].

Коэффициент при t в показателе есть частота со волны. Таким образом, в движущейся среде частота связана с волновым век­тором к соотношением

со = с£ + ик. (63,1)

Скорость распространения волн равна

это есть геометрическая сумма скорости с в направлении к и скорости и «сноса» звука вместе с движущейся жидкостью.

Определим плотность энергии звуковой волны в движущейся среде. Полная мгновенная плотность энергии дается выражением

i(Р + РО («+ v)² + + *f+PVU+ (ifl+p'uv-f ^f)

(ср. (65,1); индекс 0 у невозмущенных значений величин опу­скаем). Первый член здесь — энергия невозмущенного течения. Следующие два члена — первого порядка малости, но при усред­нении по времени они дадут величины второго порядка, свя­занные с энергией возбуждаемого волной среднего течения. Все эти члены следует опустить и, таким образом, интересующая нас плотность энергии звуковой волны как таковой дается заклю­ченными в скобки тремя последними членами. Скорость и из­менение давления в плоской волне в движущейся среде свя­заны соотношением

(со — ku) v = kc²p'/p, которое следует из линеаризованного уравнения Эйлера

ir + (^uv)v=—L_Vp.

Учитывая также (68,1), найдем окончательно, что плотность звуковой энергии в движущейся среде:

^{£ = £}о^к7' <⁶⁸'³>

*) Эта формула наглядно истолковывается с квантовой точки зренияг число звуковых квантов (фононов) N — Е/Ла = Ео1й((а— ku) не зависит от выбора системы отсчета.

где Ео = с²р'²/р=; р'²/рс² — плотность энергии в системе отсчета, движущейся вместе со средой ').

увеличении скорости и. При и cos в > с согласно формуле (68,5) «а делается отрицательной, что соответствует тому, что слыши­мый наблюдателем звук будет в действительности доходить до него в обратном порядке, т. е. звук, излученный источником в более поздние моменты времени, дойдет до наблюдателя раньше, чем звук, излученный в более ранние моменты.

Как было указано в начале § 67, приближение геометриче­ской акустики соответствует случаю достаточно малых длин волн, т. е. больших значений волнового вектора. Для этого, во­обще говоря, частота звука должна быть достаточно велика. Од­нако в акустике движущихся сред последнее условие становится не обязательным, если скорость движения среды превосходит скорость звука. Действительно, в этом случае k может быть большим даже при равной нулю частоте: из (68,1) получаем при (0 = 0 уравнение

ck = — uk, (68,6)

которое имеет решения, если и> с. Таким образом, в среде, движущейся со сверхзвуковыми скоростями, могут существовать стационарные малые возмущения, описывающиеся (при доста­точно больших k) геометрической акустикой. Это значит, что такие возмущения будут располагаться вдоль определенных ли­ний — лучей.

Рассмотрим, например, однородный сверхзвуковой поток, дви­жущийся с постоянной скоростью и, направление которой вы­берем в качестве оси х. Компоненты вектора к, лежащего в пло­скости х, у, связаны соотношением

{и — с²) k²_x = ck\, (68,7)

получающимся путем возведения в квадрат обеих частей равен­ства (68,6). Для определения формы лучей воспользуемся урав­нениями геометрической акустики (67,4), согласно которым

^{Х 1=1} dk_x ' у ^ дк_у

Разделив одно из этих уравнений на другое, получим:

dy da/dky dx dw/dkx

Но это отношение есть согласно правилу дифференцирования не­явных функций не что иное, как производная —dk_x/dk_y (взятая при постоянной, в данном случае равной нулю частоте). Таким образом, уравнение, определяющее форму лучей по заданной зависимости между k_x и k_y, гласит:

т£—%- <^м'⁸>

Подставив сюда (68,7), получим:

dx Vи² — с²

При постоянном и это уравнение определяет два прямолиней­ных луча, пересекающих ось х под углами ±а, где sina = c/«.

К подробному изучению этих лучей мы возвратимся в газо­динамике, в которой они играют большую роль.

Задачи

Решение. Подставляя (68,1) в (67,4), получим уравнения распростра­няющихся в стационарно движущейся среде с распределением скоростей и (х, у, г), причем везде и < с. Предполагается, что скорость и заметно ме­няется лишь на расстояниях, больших по сравнению с длиной волны звука.

Решение. Подставляя (68,1) в (67,4), получим уравнения распростра­нения лучей в виде

к => — (kV) и — [к rot и],

Г = V = С-г- + U.

я

С помощью этих уравнений вычисляем с точностью до членов первого по­рядка по и производную —jj (kv); при вычислении используем равенство

if³³ 4г +^(vV)u =^{(vV) и} ~ т^(kV)

Получаем:

-^т- (kv) =• — kv [n rot и],

где n — единичный вектор в направлении v. С другой стороны, jL_{kv) = n±-(kv) + kv^-.

Поскольку п и dn/dt взаимно перпендикулярны (из п² = 1 следует, что пп = 0), то из сравнения обоих выражений находим п = [rot и, п]. Вводя элемент проходимой лучом длины dl = с dt, пишем окончательно

"^Г⁼⁼7 l^rotu> ^п1- 0>

Этим уравнением определяется форма лучей; п есть единичный вектор каса­тельной к лучу (отнюдь не совпадающий теперь с направлением kl).

2. Определить форму звуковых лучей в движущейся среде с распределе­нием скоростей и, = и (z), u„ = и_г = 0.

Решение. Раскрывая уравнение (1), находим:

dn_r п. du dn,.

_ ₌ £ 2.=0

dl с dz ' dl

(уравнение для п_г можно не писать, так как n² = 1). Второе уравнение дает

звук

ГГЛ. vm

В первом же пишем п_г — dzjdl, после чего интегрирование дает

Пх — «ля т ~—•

Эти формулы решают поставленную задачу.

Предположим, что скорость и равна нулю при г — О и возрастает по направлению вверх (duldz> 0). Если звук распространяется «против ветра* (п_х < 0), то его траектория искривляется, загибаясь вверх. При распростра­нении же «по ветру» (п_х > 0) луч искривляется, загибаясь вниз; в этом слу­чае луч, вышедший из точки г = 0 под малым углом наклона к оси к (Лхо близко к единице), поднимается лишь на конечную высоту г = г_тлк, которую можно вычислить следующим образом. На высоте Zma* луч гори­зонтален, т. е. п_г — 0. Поэтому имеем здесь:

п\ + п\» 4₀ + п_у0 + 2п_х0 j = 1,

так что

„„ » (Zmax) 2

откуда по заданной функции н(г) и начальному направлению луча п₀ можно определить z_m*x-

3. Получить выражение принципа Ферма для звуковых лучей в стацио­нарно движущейся среде.

Решение. Принцип Ферма требует минимальности интеграла ^^Л,

взятого вдоль луча между двумя заданными точками, причем к предпола­гается выраженным как функция от частоты и и направления луча п (см. II § 53). Эту функцию можно найти, исключая v и k из соотношений се = = ck -f- uk и an = ck/k -f- u. В результате принцип Ферма приобретает вид

J с и

В неподвижной среде этот интеграл сводится к обычному

§ 69. Собственные колебания

До сих пор мы рассматривали колебательное движение в не­ограниченных средах. Мы видели, в частности, что в таких сре­дах могут распространяться волны с произвольными частотами.

Положение существенно меняется для жидкости, находящей­ся в сосуде конечных размеров. Самые уравнения движения (волновые уравнения) остаются при этом, конечно, теми же, но к ним необходимо добавить теперь граничные условия, которые должны выполняться на поверхности твердых стенок (или на свободной поверхности жидкости). Мы будем рассматривать здесь только свободные колебания, происходящие при отсут­ствии переменных внешних сил (колебания, совершаемые под действием внешних сил, называют вынужденными).

Уравнения движения для ограниченной жидкости отнюдь не при всякой частоте имеют решение, удовлетворяющее соответ­

ствующим граничным условиям. Такие решения существуют лишь для ряда вполне определенных значений со. Другими сло­вами, в среде конечного объема могут происходить свободные колебания лишь с вполне определенными частотами. Их назы­вают частотами собственных колебаний, или собственными ча­стотами жидкости в данном сосуде.

Конкретные значения собственных частот зависят от формы и размеров сосуда. В каждом данном случае существует беско­нечный ряд возрастающих собственных частот. Нахождение их требует конкретного исследования уравнения движения с соот­ветствующими граничными условиями.

Что касается первой, т. е. наименьшей, из собственных ча­стот, то ее порядок величины очевиден непосредственно из сооб­ражений размерности. Единственным, входящим в задачу пара­метром с размерностью длины являются линейные размеры / тела. Ясно поэтому, что соответствующая первой собственной частоте длина волны Я] должна быть порядка величины /; по­рядок величины самой частоты coi получается делением скорости звука на К\. Таким образом,

А,1 — /, coi ~ с/1. (69,1)

Выясним характер движения при собственных колебаниях. Если искать периодическое по времени решение волнового урав­нения, скажем, для потенциала скорости, в виде <р = fо(х, у, г) ег^ш, то для ф₀ будем иметь уравнение

Д<Ро + -£<Ро = 0. (69,2)

В неограниченной среде, когда не надо учитывать никаких гра­ничных условий, это уравнение обладает как вещественными, так и комплексными решениями. В частности, оно имеет реше­ние, пропорциональное е^Лт, приводящее к потенциалу вида <j> = const eⁱ<^kr-°^>'>. Такое решение представляет собой волну, рас­пространяющуюся с определенной скоростью, или, как говорят, бегущую волну.

Но для среды конечного объема комплексные решения, во­обще говоря, не могут существовать. В этом можно убедиться путем следующего рассуждения. Уравнение, которому удовлет­воряет фо, вещественно, и то же самое относится к граничным условиям. Поэтому, если щ(х,у,г) есть решение уравнений движения, то и комплексно сопряженное ф* тоже есть решение. Поскольку, с другой стороны, решение уравнений при заданных граничных условиях, вообще говоря, однозначно¹) (с точностью до постоянного множителя), то должно быть ф* = constф₀, где

') Это может не иметь места в случае формы сосуда, обладающей вы­сокой симметрией, например, в случае шара.

ЗВУК

[гл vi ir

const — некоторая комплексная постоянная, модуль которой ра­вен единице. Таким образом, ф₀ должно иметь вид

Фо = /(*. у> ^z)^e~^la

с вещественной функцией / и вещественной постоянной а. Потен­циал ф имеет, следовательно, вид (берем вещественную часть отф₀е-'^т'):

Дата добавления: 2014-11-07