Нерівність Чебишева

ЗАКОН ВЕЛИКИХ ЧИСЕЛ

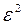Нерівність Чебишева. Ймовірність того, що відхилення випадкової величини X від її математичного сподівання по абсолютній величині менше додатного числа , не менше ніж 1 – D (X)/ визначається нерівністю

Р (|Х – М (X) |<) 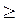1 – D (Х) / .

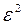98. Використовуючи нерівність Чебишева, оцінити ймовірність того, що випадкова величина X відхилиться від свого математичного сподівання менш ніж на три середніх квадратичних відхилення.

99. Використовуючи нерівність Чебишева у формі

Р (|Х – М (X) |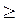) 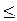D (Х) / 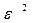, оцінити ймовірність того, що випадкова величина X відхилиться від свого математичного сподівання не менше ніж на два середніх квадратичних відхилення.

100. Використовуючи нерівність Чебишева, оцінити ймовірність того, що |Х – М (X) |< 0,2, якщо D (X)=0,004.

101. Дано: Р (|Х – М (X) |<) 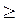0,9 і D (X)=0,009. Використовуючи нерівність Чебишева, оцінити знизу.

102. Пристрій складається з 10 незалежно працюючих елементів. Ймовірність відмови кожного елемента за час Т рівна 0,05. За допомогою нерівності Чебишева оцінити ймовірність того, що абсолютна величина різниці між числом елементів, що відмовили, і середнім числом (математичним сподіванням) відмов за час Т виявиться: а) менше двох;

б) не менше двох.

Розв’язання. а) Позначимо через X дискретну випадкову величину – число елементів, що відмовили, за час Т. Тоді

M (X) = np = 10 0,05 = 0,5;

D (X)= npq = 10 0,05 0,95 = 0,475.

Скористаємося нерівністю Чебишева: Р (|Х – М (X) |<)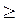1 – D (Х) /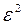

Підставивши сюди M (X)=0,5; D (X)=0,475, =2, одержимо

Р (|Х –0,5 | <2)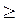1–0,475/4=0,88.

б) Події |Х –0,5 | <2 і |Х –0,5 |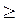 2 протилежні, тому сума їх ймовірностей рівна одиниці. Отже, Р (|Х –0,5 | 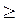2) 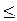1–0,88 =0,12.

103. У освітлювальну мережу паралельно підключено 20 ламп. Ймовірність того, що за час Т лампа буде включена, рівна 0,8. Використовуючи нерівність Чебишева, оцінити ймовірність того, що абсолютна величина різниці між числом включених ламп і середнім числом (математичним сподіванням) включених ламп за час Т виявиться: а) менше трьох; б) не менше трьох.

104. Ймовірність появи події А в кожному випробуванні рівна 1/2. Використовуючи нерівність Чебишева, оцінити ймовірність того, що число X появ події А міститься в межах від 40 до 60, якщо буде проведено 100 незалежних випробувань.

Розв’язання. Знайдемо математичне сподівання і дисперсію дискретної випадкової величини X – числа появ події А в 100 незалежних випробуваннях: М (Х)= np =100*0,5 =50;

D (X)= npq= 100*0,5*0,5=25.

Знайдемо максимальну різницю між заданим числом появ події і математичним сподіванням М(X)=50:

=60–50=10.

Скористаємося нерівністю Чебишева у формі

Р (|X–М (X) |<) 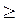1 –D (Х) / .

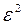Підставляючи М (X)=50, D (X)=25, =10, одержимо

Р (|X– 50 |< 10) 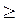1–25/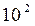 = 0,75.

105. Ймовірність появи події в кожному випробуванні рівна 1/4. Використовуючи нерівність Чебишева, оцінити ймовірність того, що число X появ події міститься в межах від 150 до 250, якщо буде проведено 800 випробувань.

106. Дискретна випадкова величина X задана законом розподілу

X 0,3 0,6

p 0,2 0,8

Використовуючи нерівність Чебишева, оцінити ймовірність того, що

| X – М (X)|<0,2.

Розв’язання. Знайдемо математичне сподівання і дисперсію величини X:

M (X) = 0,3 0,2 + 0,6 0,8 = 0,54;

D (Х) = M (X ) – [ M (Х)]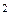= (0,3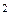0,2 + 0,6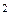0,8) – 0,54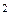= 0,0144.

Скористаємося нерівністю Чебишева у формі

Р (| X–М (X) |<) 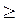1 –D (Х) / .

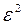Підставляючи М (X)=0,54, D (X =0,0144, = 0,2, остаточноодержимо

Р (|X– 0,54| < 0,2) 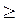1 – 0,0144/0,04 = 0,64.

107. Дискретна випадкова величина X задана законом розподілу

X 0,1 0,4 0,6

р 0,2 0,3 0,5

Використовуючи нерівність Чебишева, оцінити ймовірність того, що

| Х – M (Х)|<.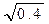

Дата добавления: 2014-10-15