
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула для гармонически спряженной функции
ГАРМОНИЧЕСКИ СОПРЯЖЕННАЯ ФУНКЦИЯ
Лекция №8
Пусть дана функция U(z), гармоническая в {| r |< 1}, для которой имеет место одно из рассматриваемых представлений. Мы приступаем к исследованию граничного поточечного поведения функции, гармонически сопряжённой с U. Ф ункция V(z) называется гармонически сопряжённой с U(z), если U(z)+iV(z)— аналитическая функция в {| r|< 1}. Сопряжённые функции определены с точностью до прибавления константы; работая в единичном круге, обычно требуют, чтобы V (0)=0; полученная таким образом гармонически сопряжённая с U(z) функция V(z) обозначается через Ũ (z). Обозначение гармонически сопряжённой функции с помощью волны („тильды") общепринято.
Предположим, что
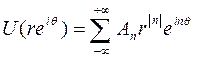 ,
, 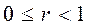
тогда
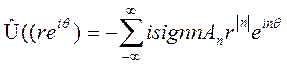
где, sign 0=0
В самом деле, функция Û(reiѲ) гармонична в единичном круге, Û(0)=0
Кроме того
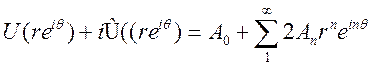
аналитическая функция в единичном круге
Теперь, если
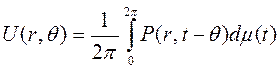
где  мера на [-π;π], то в вышеприведенном разложении функции U в ряд
мера на [-π;π], то в вышеприведенном разложении функции U в ряд 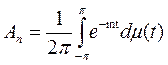 . Рассматривая разложение в ряд для Û, видим, что
. Рассматривая разложение в ряд для Û, видим, что

назовем

сопряженным ядром Пуассона. непосредственным суммированием двух геометрических прогрессий найдем, что
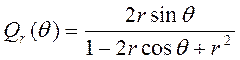
Таким образом справедлива теорема
Теорема Если 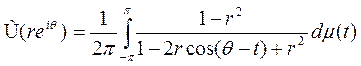 , то гармонически спряженная U функция Û задается формулой
, то гармонически спряженная U функция Û задается формулой
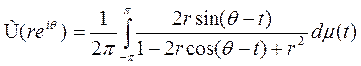
Интегральное представление классов 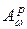
Важную роль в изучении классов 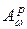 играет интегральное представление функций из этих классов.
играет интегральное представление функций из этих классов.
Сначала докажем следующее утверждение:
Теорема. Пусть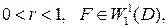 где
где 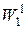 – класс Соболева в
– класс Соболева в  . Если при этом существует такое число
. Если при этом существует такое число 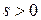 , что
, что 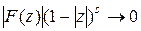 и
и  при
при 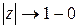 , то при всех
, то при всех 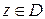 справедливо представление
справедливо представление
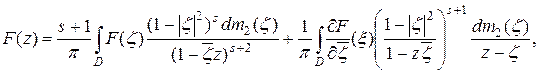 (2.5)
(2.5)
где, как обычно, 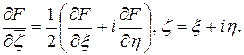
Доказательство. Пусть 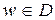 фиксировано, положим
фиксировано, положим
 Тогда, записав формулу Коши-Грина для функции
Тогда, записав формулу Коши-Грина для функции 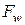 (см. [31]), имеем:
(см. [31]), имеем:
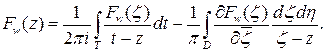
Используя условие теоремы, получаем:

Упростим подынтегральное выражение:

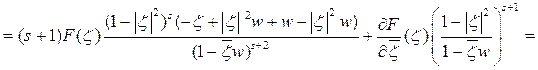
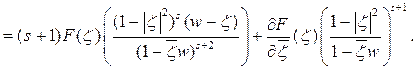
Следовательно, из равенства (2.5) имеем:
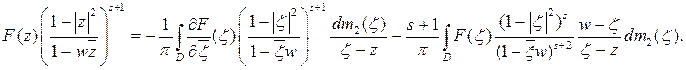
Положив  , получаем:
, получаем:
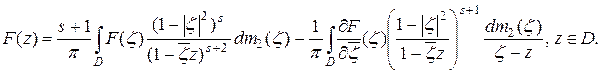 □
□
Из данной теоремы непосредственно следует:
Теорема Пусть 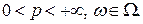 . Тогда если
. Тогда если 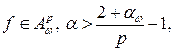 или
или  то справедливо представление
то справедливо представление

Доказательство непосредственно следует из теоремы 2.3, если учесть, что 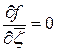 , при этом в условиях теоремы
, при этом в условиях теоремы 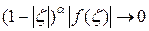 при
при 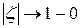 .
.
□
Из интегрального представления классов  вытекает:
вытекает:
Теорема. Пространство  при
при 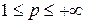 относительно нормы
относительно нормы
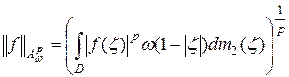
является банаховым, а при 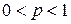 – квазибанаховым пространством.
– квазибанаховым пространством.
Доказательство. Пусть 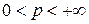 . Обозначим через
. Обозначим через 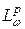 пространство измеримых в
пространство измеримых в  функций
функций 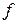 , для которых соответствующий интеграл конечен.
, для которых соответствующий интеграл конечен.
Хорошо известно, что пространство 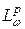 при
при 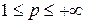 банахово, а при
банахово, а при 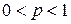 квазибанахово. Поэтому достаточно установить, что
квазибанахово. Поэтому достаточно установить, что  является замкнутым подпространством пространства
является замкнутым подпространством пространства 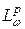 при всех
при всех 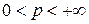 .
.
Предположим, что  – последовательность из
– последовательность из  , а функция
, а функция 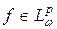 такая, что
такая, что 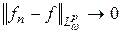 при
при 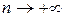 .
.
Докажем, что 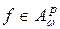 . Используя оценку (2.1), имеем:
. Используя оценку (2.1), имеем:
 .
.
Отсюда следует, что последовательность  равномерно сходится внутри
равномерно сходится внутри  к некоторой функции
к некоторой функции  . Учитывая теорему Ф. Рисса (см. [17]), нетрудно подобрать подпоследовательность
. Учитывая теорему Ф. Рисса (см. [17]), нетрудно подобрать подпоследовательность  такую, что
такую, что 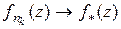 почти всюду в
почти всюду в  . Поэтому
. Поэтому  почти всюду в
почти всюду в  , и следовательно,
, и следовательно, 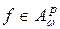 . □
. □
|
|
Дата добавления: 2014-10-15; Просмотров: 329; Нарушение авторских прав?; Мы поможем в написании вашей работы!