
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы теории корреляции
|
|
|
|
Во многих задачах требуется установит и оценить зависимость изучаемой случайной величины, например, Y от одной или нескольких других случайных величин.
Две случайные величины могут быть связаны либо функциональной зависимостью, либо статистической зависимостью, либо быть независимыми.
Строгая функциональная зависимость реализуется очень редко.
Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой.
Если статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой, то такая зависимость называется корреляционной.
Условным средним 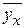 называют среднее арифметическое наблюдавшихся значений случайной величины Y, соответствующих значению х случайной величины Х, т.е. Х = х.
называют среднее арифметическое наблюдавшихся значений случайной величины Y, соответствующих значению х случайной величины Х, т.е. Х = х.
Например, если при х 1 = 2 величина Y приняла значения у 1= 5, у 2= 6, у 3= 10, то условное среднее 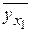 =
= 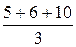 = 7.
= 7.
Условным средним 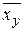 называют среднее арифметическое наблюдавшихся значений величины Х, соответствующих значению Y = y.
называют среднее арифметическое наблюдавшихся значений величины Х, соответствующих значению Y = y.
Условное среднее 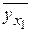 является функцией от х, т.к. при изменении х будет изменяться
является функцией от х, т.к. при изменении х будет изменяться 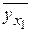 . Обозначим ее через
. Обозначим ее через 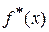 . В результате получим уравнение
. В результате получим уравнение
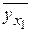 =
= 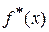 .
.
Это уравнение называют выборочным уравнением регрессии Y на Х; функцию 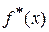 называют выборочной регрессией Y на Х, а ее график выборочной линией регрессии Y на Х.
называют выборочной регрессией Y на Х, а ее график выборочной линией регрессии Y на Х.
Аналогично, уравнение
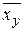 =
= 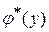
называют выборочным уравнением регрессии Х на Y; функцию 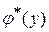 называют выборочной регрессией Х на Y, а ее график выборочной линией регрессии Х на Y.
называют выборочной регрессией Х на Y, а ее график выборочной линией регрессии Х на Y.
Выборочное уравнение прямой линии регрессии по несгруппированным данным
Пусть изучается система количественных признаков (Х, Y). Пусть в результате п независимых опытов получены п пар чисел (х 1, у 1), (х 2, у 2), …, (хп, уп). По этим наблюдениям найдем выборочное уравнение прямой линии регрессии Y на Х:
|
|
|
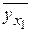 =
= 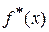 = kx + b.
= kx + b.
Так как различные значения х признака Х и соответствующие им значения у признака Y наблюдались по одному разу, то группировать данные нет необходимости. Так же нет надобности использовать понятие условной средней. Поэтому искомое уравнение можно записать в виде
Y = kx + b
или
Y =  x + b, (1)
x + b, (1)
где  − выборочный коэффициент регрессии Y на Х.
− выборочный коэффициент регрессии Y на Х.
Рассмотрим разность (отклонение)
Yi – yi,
где Yi – вычисленная по уравнению (1) ордината, соответствующая наблюдаемому значению хi; yi - наблюдаемая ордината, соответствующая наблюдаемому значению хi.
Чем меньше отклонение Yi – yi, тем ближе точки (х 1, у 1), (х 2, у 2), …, (хп, уп), построенные по данным наблюдений, на плоскости ХОY к прямой (1).
Подберем параметры  и b так, чтобы сумма квадратов отклонений была минимальной (в этом состоит сущность метода наименьших квадратов). Для этого построим функцию
и b так, чтобы сумма квадратов отклонений была минимальной (в этом состоит сущность метода наименьших квадратов). Для этого построим функцию
F ( , b) =
, b) = 
или
F ( , b) =
, b) = 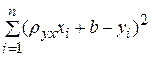
Для отыскания минимума функции приравняем нулю частные производные
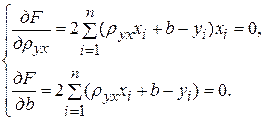
Выполнив элементарные преобразования, получим систему двух линейных уравнений относительно  и b:
и b:
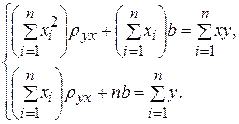 (2)
(2)
Решив эту систему, найдем искомые параметры  и b, а значит, и выборочное уравнение прямой линии регрессии Y на Х:
и b, а значит, и выборочное уравнение прямой линии регрессии Y на Х:
Y =  x + b.
x + b.
Аналогично можно найти выборочное уравнение прямой линии регрессии Х на Y:
Х = 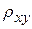 у + с,
у + с,
где 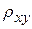 − выборочный коэффициент регрессии Х на Y.
− выборочный коэффициент регрессии Х на Y.
Пример. Найти выборочное уравнение прямой линии регрессии Y на Х по данным, п = 5, наблюдений:
х 1 1,5 3 4,5 5
у 1,25 1,4 1,5 1,75 2,25.
□
| xi | yi | 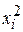
| xiyi |
| 1,25 | 1,25 | ||
| 1,5 | 1,4 | 2,25 | 2,1 |
| 1,5 | 4,5 | ||
| 4,5 | 1,75 | 20,25 | 7,875 |
| 2,25 | 11,25 | ||
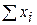 =15 =15
| 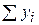 =8,15 =8,15
| 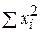 =57,5 =57,5
| 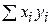 =26,975 =26,975
|
Составим расчетную таблицу:
По данным суммирования составим систему уравнений
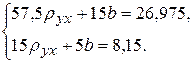
Решая систему, найдем
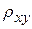 = 0,202, b = 1,024.
= 0,202, b = 1,024.
Искомое уравнение регрессии:
|
|
|
Y = 0,202 x + 1,024.
Для того, чтобы получить представление, насколько хорошо вычисленные по этому уравнению значения Yi согласуются с наблюдаемыми значениями уi, найдем отклонения Yi – yi:
| xi | Yi | yi | Yi − yi |
| 1,226 | 1,25 | −0,024 | |
| 1,5 | 1,327 | 1,4 | −0,073 |
| 1,630 | 1,5 | 0,130 | |
| 4,5 | 1,933 | 1,75 | 0,183 |
| 2,034 | 2,25 | −0,216 |
Из таблицы видно, что не все отклонения достаточно малы. Это объясняется малым числом наблюдений.
Построим график регрессии и вынесем на плоскость наблюдаемые точки:
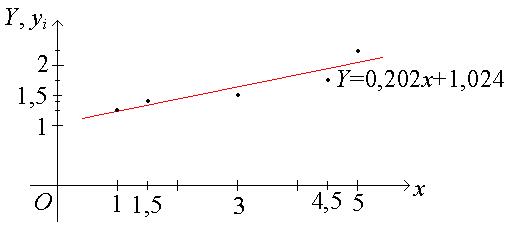
■
Выборочное уравнение прямой линии регрессии по сгруппированным данным
При большом числе наблюдений одно и то же значение х может встретиться пх раз; одно и то же значение у − пу раз; одна и та же пара чисел (х, у) может наблюдаться пху раз. Поэтому данные наблюдений группируют, т.е. подсчитывают частоты пх, пу и пху. Все сгруппированные данные записывают в виде таблицы, называемую корреляционной:
| Y X | х 1 | х 2 | … | xq | пу |
| у 1 | 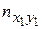
| 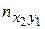
| … | 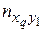
| 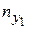
|
| у 2 | 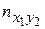
| 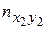
| … | 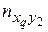
| 
|
| … | … | … | … | … | … |
| yp | 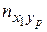
| 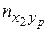
| … | 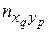
| 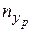
|
| пх | 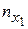
| 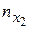
| … | 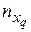
| n |
В 1-й строке таблицы указаны наблюдаемые значения признака Х, а в 1-м столбце – наблюдаемые значения признака Y. На пересечении строк и столбцов находятся частоты пху наблюдаемых пар значений признаков.
В последнем столбце записаны суммы частот строк. Например, 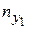 − число наблюдений значения у 1 признака Y в сочетании с различными значениями признака Х.
− число наблюдений значения у 1 признака Y в сочетании с различными значениями признака Х.
В последней строке записаны суммы частот столбцов.
В клетке, расположенной в нижнем правом углу таблицы – сумма всех частот. Очевидно, что 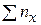 =
=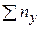 = п.
= п.
Составим выборочное уравнение прямой линии регрессии по сгруппированным данным. Для этого используем систему (2), полученную в предыдущем пункте
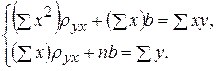 (2)
(2)
Воспользуемся тождествами:
из 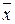 =
= 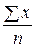 следует
следует 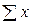 = п
= п 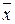 ;
;
из 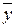 =
= 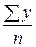 следует
следует 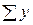 = п
= п 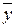 ;
;
из 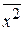 =
= 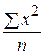 следует
следует 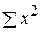 = п
= п 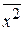
и
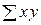 =
= 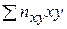 (учтено, что пара чисел (х, у) наблюдалась пху раз).
(учтено, что пара чисел (х, у) наблюдалась пху раз).
Подставляя в систему (2) и сократив второе уравнение на п, получим
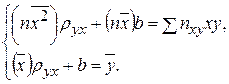 (3)
(3)
Решив эту систему, найдем параметры  и b, а значит, искомое уравнение прямой линии регрессии Y на Х:
и b, а значит, искомое уравнение прямой линии регрессии Y на Х:
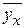 =
=  x + b. (4)
x + b. (4)
Но на практике уравнение (4) используют в другом виде.
Найдем b из второго уравнения системы (3):
b = 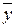 −
−
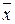 . (5)
. (5)
Подставляя (5) в уравнение (4), получим
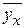 −
− 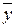 =
=  (х −
(х − 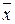 ). (6)
). (6)
|
|
|
Подставим (5) в первое уравнение системы (3) и найдем коэффициент регрессии  :
:
п 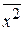
 + п
+ п 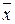 b =
b = 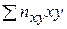 ,
,
п 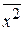
 + п
+ п 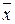 (
(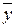 −
−
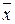 ) =
) = 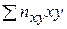 ,
,
п 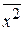
 + п
+ п 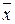
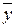 − n
− n 
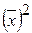 =
= 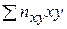 ,
,
n  (
(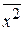 −
− 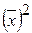 ) =
) = 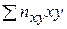 − п
− п 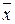
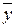 ,
,
 =
= 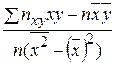
или
 =
= 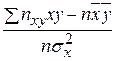 .
.
Умножим обе части этого равенства на 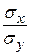 :
:
 ·
·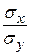 =
= 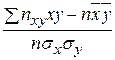 . (7)
. (7)
Назовем
r в = 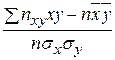
выборочным коэффициентом корреляции.
Подставляем r в в (7):
 ·
·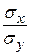 = r в.
= r в.
Отсюда
 = r в
= r в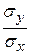 .
.
Подставляя  в уравнение (6), получим выборочное уравнение прямой линии регрессии Y на Х
в уравнение (6), получим выборочное уравнение прямой линии регрессии Y на Х
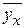 −
− 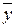 = r в
= r в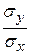 (х −
(х − 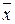 ).
).
Аналогично находят выборочное уравнение прямой линии регрессии Х на Y
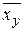 −
− 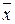 = r в
= r в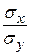 (у −
(у − 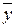 ).
).
Если обе линии регрессии Y на Х и Х на Y – прямые, то корреляцию называют линейной.
Выборочный коэффициент корреляции
Выборочный коэффициент корреляции r в вычисляется по формуле
r в = 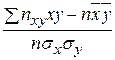 .
.
Свойства:
10. Значения r в заключены в отрезке [−1, 1], т.е. −1 ≤ r в ≤ 1 или | r в | ≤ 1.
20. Если признаки Х и Y рассматривать в качестве случайных величин, то из их независимости следует r в = 0. Обратное утверждение в общем случае неверно.
30. Если | r в | = 1, то Х и Y связаны линейной функциональной зависимостью.
Если значение | r в | близко к единице, то надо находить линейную функцию регрессии.
Если | r в | < 0,5, то обычно не стоит использовать линейную функцию. В этом случае можно попробовать найти нелинейную функцию (параболическую, гиперболическую, степенную, показательную).
Выборочный коэффициент корреляции служит для оценки силы линейной корреляционной связи:
чем ближе | r в | к единице, тем связь сильнее;
чем ближе | r в | к нулю, тем связь слабее.
Если r в>0, то связь прямая; если r в< 0, то связь обратная.
Выборочный коэффициент корреляции r в является оценкой коэффициента корреляции r г генеральной совокупности.
Проверка гипотезы о значимости выборочного коэффициента корреляции
Пусть двумерная генеральная совокупность (Х, Y) распределена нормально. Из этой совокупности извлечена выборка объема п и по ней найден выборочный коэффициент корреляции r в ≠ 0. Требуется проверить нулевую гипотезу Н 0: r г = 0 о равенстве нулю генерального коэффициента корреляции.
Если нулевая гипотеза принимается, то это означает, что выборочный коэффициент корреляции r в незначим, т.е. генеральный коэффициент корреляции r гнезначимо отличается от нуля. В этом случае Х и Y некоррелированы, т.е. не имеют корреляционной связи; в противном случае − выборочный коэффициент корреляции r в значим, т.е. генеральный коэффициент корреляции r гзначимо отличается от нуля. В этом случае Х и Y коррелированы, т.е. имеют корреляционную связь.
|
|
|
Правило проверки гипотезы Н 0
Для того, чтобы при уровне значимости  проверить гипотезу Н 0: r г= 0 при конкурирующей гипотезе Н 1: r г≠ 0, надо:
проверить гипотезу Н 0: r г= 0 при конкурирующей гипотезе Н 1: r г≠ 0, надо:
1. Вычислить наблюдаемое значение критерия Стьюдента
Тнабл. = 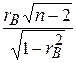
(иногда вместо объема выборки п в формуле ставят N – максимальное число интервалов для Х или для Y).
2. По таблице критических точек распределения Стьюдента, по заданному уровню значимости  и числу степеней свободы k = п – 2 (k = N – 2) найти критическую точку tкр. (
и числу степеней свободы k = п – 2 (k = N – 2) найти критическую точку tкр. ( , k) двусторонней критической области.
, k) двусторонней критической области.
3. Если | Тнабл. | < tкр., то нет оснований отвергать гипотезу Н 0.
Если | Тнабл. | > tкр., то гипотезу Н 0 отвергают.
Пример. В результате 78 опытов получены значения признаков Х и Y:
| X | Y | X | Y | X | Y | X | Y |
| -291 | -219 | -241 | -264 | ||||
| -270 | -281 | -243 | -240 | ||||
| -279 | -262 | -245 | -277 | ||||
| -282 | -302 | -282 | -279 | ||||
| -254 | -275 | -252 | -253 | ||||
| -264 | -267 | -276 | -275 | ||||
| -216 | -290 | -276 | -248 | ||||
| -276 | -266 | -246 | -243 | ||||
| -248 | -283 | -284 | -264 | ||||
| -253 | -237 | -271 | -267 | ||||
| -276 | -222 | -227 | -213 | ||||
| -262 | -281 | -256 | -218 | ||||
| -234 | -269 | -309 | -223 | ||||
| -313 | -257 | -300 | -278 | ||||
| -278 | -235 | -310 | -236 | ||||
| -292 | -275 | -255 | -263 | ||||
| -271 | -276 | -252 | -268 | ||||
| -256 | -282 | -274 | -243 | ||||
| -291 | -277 | -291 | -271 | ||||
| -243 | -270 |
1. Составить корреляционную таблицу, используя результаты всех экспериментов.
2. Найти выборочные уравнения регрессии и построить их графики.
3. Проверить гипотезу о значимости выборочного коэффициента корреляции и наличии корреляционной связи между признаками Х и Y при уровне значимости  = 0,05.
= 0,05.
□
1. Найдем минимальные и максимальные значения Х и Y:
x min= 55, x max= 80;
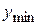 = −313,
= −313, 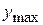 = −213.
= −213.
Пусть началами первых интервалов будут: х 1= 53 для Х, у 1= −321 для Y. Составим корреляционную таблицу с шагом h 1 = 6 для Х, h 2 = 20 для Y. Для каждой пары чисел (хi, yj) определяем в какой столбец попало значение хi и в какую строку попало ему соответствующее значение yj. В клетку, расположенную на пересечении найденной строки и столбца ставим некоторый знак. Операцию проводим для всех пар.
| Y X | [53,59) | [59,65) | [65,71) | [71,77) | [77,83) |
| [-321, -301) | 
| 
| |||
| [-301, -281) | 
| 
| |||
| [-281, -261) | 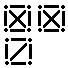
| 
| |||
| [-261, -241) |  
| 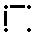
| |||
| [-241, -221) |  
| 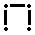
| |||
| [-221, -201) | 
|
Вычислим середины частичных интервалов:
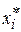 =
= 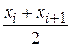 ,
, 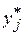 =
= 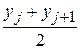 ;
;
подсчитаем количество знаков в каждой клетке; добавим столбец пу и строку пх. В результате получим корреляционную таблицу
| Y X | пу | |||||
| −311 | ||||||
| −291 | ||||||
| −271 | ||||||
| −251 | ||||||
| −231 | ||||||
| −211 | ||||||
| пх | п =78 |
2. Составим выборочное уравнение регрессии Y на Х:
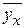 −
− 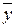 = r в
= r в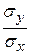 (х −
(х − 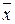 ).
).
Выборочный коэффициент корреляции:
r в = 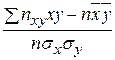 .
.
Найдем, используя корреляционную таблицу, параметры, входящие в эти выражения:
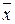 =
= 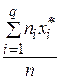 =
= 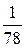 ·(6·56 + 18·62 + 35·68 +15·74 + 4·80) = 67,462;
·(6·56 + 18·62 + 35·68 +15·74 + 4·80) = 67,462;
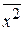 =
= 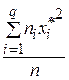 =
= 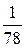 ·(6·562 + 18·622 + 35·682 +15·742 + 4·802) = 4584,462;
·(6·562 + 18·622 + 35·682 +15·742 + 4·802) = 4584,462;
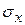 =
=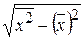 =
=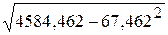 = 5,774;
= 5,774;
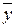 =
= 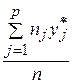 =
=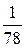 ·(4·(-311)+11·(-291)+ 33·(-271)+17·(-251)+9·(-231)+4·(-211)) =
·(4·(-311)+11·(-291)+ 33·(-271)+17·(-251)+9·(-231)+4·(-211)) =
= −263,821;
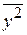 =
= 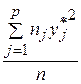 =
=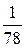 ·(4·(-311)2+11·(-291)2+33·(-271)2+17·(-251)2+9·(-231)2+4·(-211)2) =
·(4·(-311)2+11·(-291)2+33·(-271)2+17·(-251)2+9·(-231)2+4·(-211)2) =
= 70144,59;
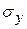 =
=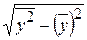 =
= 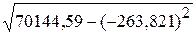 = 23,304;
= 23,304;
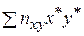 =1·74·(-311)+3·80·(-311)+10·74·(-291)+1·80·(-291)+29·68·(-271)+4·74·(-271)+
=1·74·(-311)+3·80·(-311)+10·74·(-291)+1·80·(-291)+29·68·(-271)+4·74·(-271)+
+11·62·(-251)+6·68·(-251)+2·56·(-231)+7·62·(-231)+4·56·(-211) = 1397882.
Найдем выборочный коэффициент корреляции
r в = 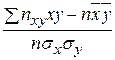 =
= 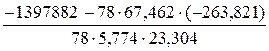 = −0,919.
= −0,919.
Уравнение регрессии Y на Х:
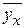 −
− 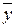 = r в
= r в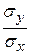 (х −
(х − 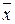 )
)
или
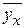 =
= 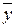 + r в
+ r в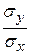 (х −
(х − 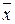 ).
).
Тогда
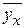 = −263,821 + (−0,919)
= −263,821 + (−0,919) 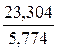 (х − 67,462)
(х − 67,462)
или
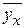 = −3,709 х − 13,604. (а)
= −3,709 х − 13,604. (а)
Уравнение регрессии Х на Y:
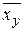 −
− 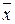 = r в
= r в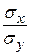 (у −
(у − 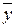 )
)
или
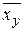 =
= 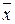 + r в
+ r в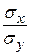 (у −
(у − 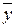 ).
).
Тогда
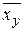 = 67,462 + (−0,919)
= 67,462 + (−0,919) 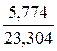 (у +263,821)
(у +263,821)
или
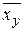 = −0,228 у + 7,390. (б)
= −0,228 у + 7,390. (б)
Построим графики этих регрессий:

Графики должны пересекаться в точке (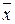 ,
, 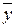 ), т.е. в точке (67,462; −263,821).
), т.е. в точке (67,462; −263,821).
3. Проверим гипотезу о значимости выборочного коэффициента корреляции.
По правилу проверки гипотезы Н 0:
1. Наблюдаемое значение критерия Стьюдента
Тнабл. = 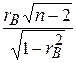 =
= 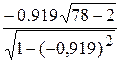 =
= 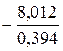 = −20,335.
= −20,335.
2. Критическая точка tкр. ( , k) двусторонней критической области:
, k) двусторонней критической области:
tкр. ( , п– 2) = tкр. (0,05;78–2) = tкр. (0,05;76) = 1,99.
, п– 2) = tкр. (0,05;78–2) = tкр. (0,05;76) = 1,99.
3. Так как | Тнабл. |> tкр (|−20,335|>1,99), то гипотезу Н 0 отвергаем. Значит, выборочный коэффициент корреляции r в значим, т.е. генеральный коэффициент корреляции r гзначимо отличается от нуля. В этом случае Х и Y коррелированы, т.е. имеют корреляционную связь.
■
Замечание. При решении задач можно перейти к условным вариантам:
ui = 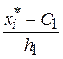 , vj =
, vj = 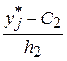 ,
,
где С 1 и С 2 – значения 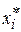 и
и 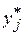 , соответствующие максимальной частоте пху. Желательно, чтобы клетка с данной частотой находилась в середине таблицы. Точку (С 1, С 2) называют ложным нулем. В этом случае новые переменные U и V будут принимать значения: 0, ±1, ±2, ….
, соответствующие максимальной частоте пху. Желательно, чтобы клетка с данной частотой находилась в середине таблицы. Точку (С 1, С 2) называют ложным нулем. В этом случае новые переменные U и V будут принимать значения: 0, ±1, ±2, ….
Выборочный коэффициент корреляции:
r в = 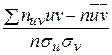 .
.
Величины 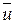 ,
, 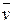 ,
, 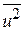 ,
, 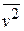 ,
, 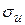 ,
, 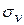 вычисляются по формулам:
вычисляются по формулам:
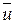 =
= 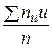 ,
, 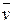 =
= 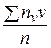 ,
,
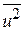 =
=  ,
, 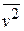 =
= 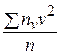 ,
,
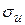 =
= ,
, 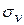 =
=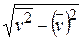 .
.
Зная эти величины, можно определить входящие в уравнения регрессии величины по формулам:
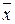 =
= 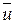 h 1 + C 1,
h 1 + C 1, 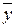 =
= 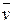 h 2 + C 2,
h 2 + C 2,
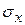 =
= 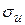 h 1,
h 1, 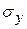 =
= 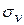 h 2.
h 2.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 896; Нарушение авторских прав?; Мы поможем в написании вашей работы!