Оценка точности модели

Наряду с характеристиками адекватности модели при оценивании качества модели необходимо учитывать ее точность.

Как правило, о точности модели и прогноза судят по величине погрешности (ошибки). Ошибка прогноза это расхождение между фактическим и прогнозируемым значением исследуемого показателя. Использование данного подхода к оценке точности возможно только в том случае, когда период упреждения закончился, и исследователи имеют фактические значения на период упреждения или когда разрабатывается ретропрогноз.

Ретроспективное прогнозирование разрабатывается для некоторого момента времени в прошлом, для которого имеются фактические данные. В этом случае имеющаяся информация делится на две части. Первая часть, включающая более ранние данные, используется для подбора математической модели. По построенной математической модели дается прогноз на последующий оставшийся период времени. Прогнозные качества модели оцениваются по более поздним данным второй части ряда. Полученные ошибки прогноза в какой-то мере харак­теризуют точность подобранных моделей и могут использоваться при сопоставлении различных моделей прогнозирования. В то же время при использовании ошибки ретроспективного прогноза в качестве меры точности необходимо учитывать, что она получена при использовании только части имеющихся данных. При использовании полного объема имеющихся данных трансформируется вид подобранной модели, и изменяются значения критериев точности и качества.

Отметим, что если ретроспективное прогнозирование осуществляется по модели, содержащей одну или несколько экзогенных пере­менных, точность прогноза будет определяться точностью определения значения этих переменных на пе­риод упреждения. В этом случае возможны два способа определения значений экзогенных переменных: либо воспользоваться фактическими известными значениями экзогенных переменных либо ожидаемыми их значениями. Естественно, что точность прогноза в первом случае будет выше.

Наличие данных о реализации прогнозов дает возможность оценить качество прогнозов величиной:

,

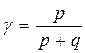где р – число прогнозов, подтвержденных фактическими данными (фактическая реализация охвачена интервальным прогнозом);

q – число прогнозов, не подтвержденных фактическими данными.

Использование коэффициентов 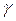для разных моделей имеет смысл в том случае, если доверительные вероятности прогнозов приняты одинаковыми.

В том случае, если прогноз дается в виде точечной оценки, в качестве показателей точности прогноза могут использоваться такие статистические характеристики как средняя абсолютная и среднеквадратическая ошибка прогноза.

Г. Тейлом предложен в качестве меры качества прогноза коэффициент расхождения (или коэффициент несоответствия):

,

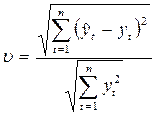где 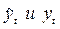- соответственно предсказанное и фактическое значение переменной. Коэффициент 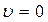, когда 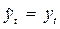(случай совершенного прогнозирования). Коэффициент 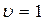, когда экстраполяция строится исходя из неизменности приростов. Коэффициент 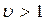, прогноз дает худшие результаты, чем прогноз методом простой экстраполяции.

Рассмотренные выше показатели точности прогноза можно использовать только в случае наличия истинных значений величин, оцениваемых при разработке прогноза. Согласно этому различают апостериорную точность моделей, которая может быть определена только после практического использова­ния модели, и априорную точность моделей. Априорную или предполагаемую точность оценива­ют в условиях отсутствия информации о результатах эксплуа­тации модели. Исследуя априорную точность модели, мы охарактеризуем только точность аппроксимации.

Чаще всего в качестве показателей точности применяются следующие показатели: абсолютная ошибка 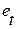, средняя абсолютная ошибка 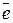, средняя квадратическая ошибка 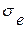, относительная ошибка 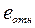, средняя относительная ошибка 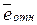, коэффициент сходимости, коэффициент детерминации

Абсолютная ошибка прогноза определяется как раз­ность между фактическим значением и его оценкой, полученной расчетным путем по модели:

,

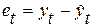среднее абсолютное значение ошибки:

.

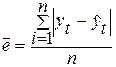Средняя квадратическая ошибка прогноза рассчитывается по формуле:

,

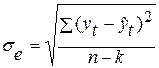где п — период упреждения,

k – число оцениваемых параметров модели.

Недостатком рассмотренных характеристик является их зависимость от масштаба измерения значений исследуемого показателя.

В связи с этим более удобными являются относительные значения этих величин. Относительная ошибка рассчитывается следующим образом:

,

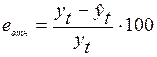а средняя относительная ошибка определяется следующим образом:

.

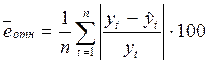Последний показатель чаще других используется при сравнении точности прогнозов, осуществляемых по различным методикам. Обычно лучшим признается тот прогноз, который имеет меньшее значение этого показателя. Принято считать, что если значение средней относительной ошибки менее 3-5%, то точность хорошая; если значение средней относительной ошибки не превышает 10%, то точность хорошая; от 10% до 15% точность удовлетворительная.

Коэффициент сходимости определяется по следующей формуле:

,

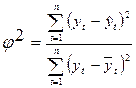чем меньше значение коэффициента сходимости, чем лучше точность модели.

Коэффициент детерминации определяется по формуле:

,

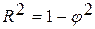и поэтому чем больше значение коэффициента детерминации, тем лучше точность модели.

Для выбора лучшей модели можно использовать один из рассмотренных показателей либо воспользоваться обобщенным критерием.

Пример. Оценить адекватность и точность модели Хольта, построенной в параграфе 5.3.

Решение. В таблице 5.2 приведены ошибки аппроксимации 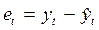, на основе которых будет оцениваться адекватность модели. Проверку случайности колебаний уровней остаточной компоненты проведем, используя критерий поворотных точек. На рис. 6.2 представлен ряд остатков, количество поворотных точек равно 15.

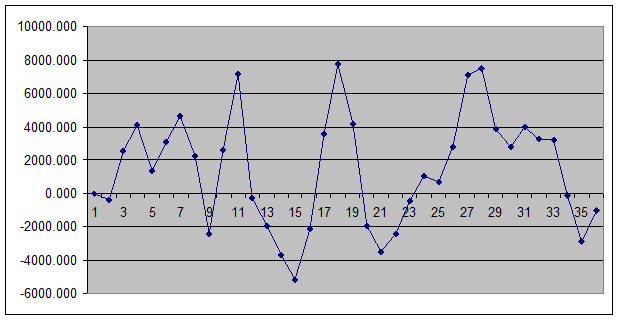
Рис. 6.2. Оценка адекватности модели. Ряд остатков.

При n=36: 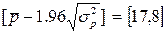. Неравенства 15>17 не выполняется, следовательно, ряд остатков не является случайным.

Анализ соответствия ряда остатков нормальному закону распределения проведем по RS – критерию:

.

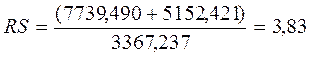Расчетное значение RS – критерия сравним с табличными значениями RS – критерия (таб. 6.1). Расчетное RS – критерия попадает в интервал, ограниченный табличными значениями (3,6; 5,06), и с уровнем значимости α=0,05 гипотеза о нормальности распределения остаточной компоненты принимается.

Так как остаточная компонента распределена по нормальному закону, то осуществим проверку равенства математического ожидания остаточной компоненты нулю с помощью t-критерия Стьюдента:

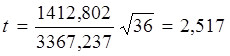Расчетное значение t -критерия больше табличного значения t_α статистики Стьюдента 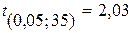, следовательно, гипотеза о равенстве нулю математического ожидания уровней ряда остатков не принимается.

Независимость уровней в ряде остатков проверим по критерию Дарбина–Уотсона (таб. 6.3).

Таблица 6.3

Расчет d- значения Дарбина–Уотсона

t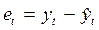
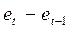
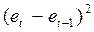
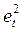
	-23.500			552.25
	-415.390	-391.890	153577.772	172548.852
	2553.781	2969.171	8815978.8	6521799.44
	4108.015	1554.234	2415642.82	16875789.2
	1357.017	-2750.998	7567992.09	1841494.74
	3047.488	1690.471	2857692.36	9287182.51
	4611.776	1564.288	2446997.23	21268477.8
	2226.788	-2384.988	5688168.37	4958584.19
	-2442.290	-4669.078		5964779.36
	2620.809	5063.099	25634971.3	6868640.89
	7156.526	4535.717	20572724.5	51215860.7
	-255.774	-7412.299	54942183.2	65420.1907
	-1964.630	-1708.857	2920190.74	3859772.09
	-3692.014	-1727.384	2983855.54	13630969.5
	-5152.421	-1460.407	2132789.2	26547447.2
	-2101.028	3051.394	9311004.57	4414317.05
	3571.246	5672.274	32174688.1	12753798.1
	7739.490	4168.244	17374260.7	59899710.6
	4171.509	-3567.981	12730490.5	17401487.7
	-1955.050	-6126.559	37534730.7	3822222.1
	-3465.610	-1510.560	2281790.33	12010452.8
	-2395.256	1070.354	1145657.1	5737252.69
	-445.847	1949.410	3800197.94	198779.235
	1050.970	1496.817	2240461.18	1104538.71
	694.152	-356.818	127319.3	481847.09
	2752.621	2058.469	4237296.08	7576924.68
	7090.334	4337.713	18815752.4	50272839.5
	7485.321	394.987	156014.473
	3824.177	-3661.144	13403973.2	14624331.3
	2773.655	-1050.522	1103597.19	7693161.27
	3953.251	1179.597	1391448.08	15628196.9
	3253.170	-700.082	490114.569	10583112.5
	3170.670	-82.500	6806.172	10053148.7
	-134.635	-3305.305	10925041.8	18126.5898
	-2869.411	-2734.776	7478999.31	8233519.15
	-1039.034	1830.377	3350281.25	1079590.8
сумма

Расчетное d- значение равно:

.

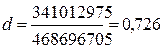Расчетное значение d- критерия сравним с двумя табличными значениями Дарбина—Уотсона (1,41; 1,52). Так как расчетное d -значение меньше нижнего табличного значения d₁ =1,41, то гипотеза о независимости ряда остатков отвергается и модель неадекватна.

Результаты оценки модели на адекватность приведены в таблице 6.4.

Таблица 6.4

Результаты оценки модели на адекватность

Проверяемое свойство	вывод
Случайность	неадекватна
Нормальность	адекватна
Среднее	неадекватна
Независимость	неадекватна
Вывод: модель статистически неадекватна

Средняя относительная ошибка равна (таб. 5.2):

.

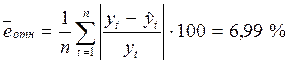Оцениваемая модель не является адекватной, и несмотря на хорошую точность не может использоваться для прогнозирования.

Контрольные вопросы и задания

1. Когда модель считается адекватной экономическому процессу?

2. Какие свойства остаточной компоненты проверяются при оценке адекватности модели? Какие статистические критерии при этом используются?

3. Поясните суть ретроспективного прогнозирования.

4. Какие статистические характеристики используются для оценки точности модели?

5. По результатам выполнения задания 9 (глава 5) оценить адекватность и точность модели Брауна с параметром сглаживания α=0,2 и α=0,6.

Глава 7. Применение регрессионных моделей для прогнозирования

Дата добавления: 2014-10-22