
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальное распределение. Если плотность распределения (дифференциальная функция) случайной переменной определяется выражением:
|
|
|
|
Если плотность распределения (дифференциальная функция) случайной переменной определяется выражением:
 (5.10)
(5.10)
то говорят, что Х имеет нормальное распределение с параметрами а и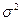 . Вероятностный смысл параметров:
. Вероятностный смысл параметров: 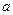 =М(X), а
=М(X), а 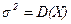 . Обозначение:
. Обозначение:
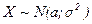
Для расчета вероятности попадания нормально распределенной случайной величины Х в промежуток от 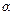 до
до 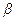 используется формула:
используется формула:
 (5.11)
(5.11)
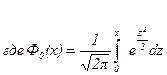 (интеграл Лапласа)
(интеграл Лапласа)
Формула (5.11) иногда в литературе называется интегральной теоремой Лапласа.
Функция  обладает свойствами:
обладает свойствами:

3 ) (см. таблицу приложения 2).
(см. таблицу приложения 2).
Функция  табулирована. В частности для симметричного относительно а промежутка
табулирована. В частности для симметричного относительно а промежутка 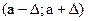 имеем:
имеем:
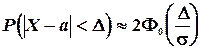 (5.12)
(5.12)
Формула (5.12) применима и к частоте m, поскольку ее закон распределения при достаточно большом числе испытаний практически совпадает с нормальным. Применительно к случайной величине m, с учетом ее числовых характеристик
M(m) = np и 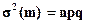 (5.13)
(5.13)
формула (5.12) примет вид:
 (5.14)
(5.14)
Формула (5.12) может быть применена и к относительной частоте 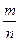 с числовыми характеристиками
с числовыми характеристиками  и
и 
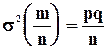
 (5.15)
(5.15)
 (5.16)
(5.16)
С вероятностью, очень близкой к единице (равной  нормально распределенная случайная величина Х удовлетворяет неравенству:
нормально распределенная случайная величина Х удовлетворяет неравенству:
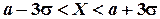 (5.17)
(5.17)
В этом состоит правило трех сигм: если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает  .
.
Локальная теорема Муавра-Лапласа. При р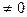 и p
и p 1 и достаточно большом n биноминальное распределение близко к нормальному закону (причем их математические ожидания и дисперсии совпадают), т.е. имеет место равенство:
1 и достаточно большом n биноминальное распределение близко к нормальному закону (причем их математические ожидания и дисперсии совпадают), т.е. имеет место равенство:
 , где
, где 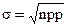 , a =nр
, a =nр
Тогда:
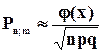 (5.18)
(5.18)
для достаточно больших n (здесь  (х) - плотность вероятностей стандартной нормальной случайной величины
(х) - плотность вероятностей стандартной нормальной случайной величины  и
и 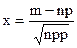 ).
).
|
|
|
Пример 5.1. На рынок поступила крупная партия говядины. Предполагается, что вес туш - случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием а = 950 кг и средним квадратическим отклонением s = 150 кг. Определите вероятность того, что вес случайно отобранной туши:
а) окажется больше 1250 кг;
б) окажется меньше 850 кг;
в) будет находиться между 800 и 1300 кг;
г) отклонится от математического ожидания меньше, чем на 50 кг;
д) отклонится от математического ожидания больше, чем на 50 кг;
е) Найдите границы, в которых отклонение веса случайно отобранной туши от своего математического ожидания не превысит утроенного среднего квадратического отклонения (проиллюстрируйте правило трех сигм);
ж) С вероятностью 0,899 определите границы, в которых будет находиться вес случайно отобранной туши. Какова при этом условии максимальная величина отклонения веса случайно отобранной туши от своего математического ожидания?
Решение. а) Вероятность того, что вес случайно отобранной туши окажется больше 1250 кг – можно понимать как вероятность того, что вес случайно отобранной туши окажется в интервале от 1250 кг до +∞.
Формула расчета вероятности попадания в заданный интервал нормально распределенной случайной велечины Х имеет вид:
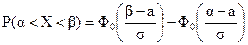 ,
,
где Ф0(z) - функция Лапласа:

Функция Ф0(z) является нечетной функцией; т.е. Ф0(-z) = -Ф0(z).
Найдем вероятность того, что вес случайно отобранной туши окажется больше 1250 кг. По условию: a = 1250, b = +¥, а = 950, s = 150.
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 913; Нарушение авторских прав?; Мы поможем в написании вашей работы!